Analistas mejoran representaciones de estructuras financieras con las capacidades simbólicas de Mathematica

Ahora más que nunca, la computación financiera implica más que un puro procesamiento de números, de modo que los nuevos líderes financieros recurren a Mathematica para asistencia.

Las casas de inversiones regularmente dividen títulos tales como hipotecas, bonos del gobierno e, incluso, bonos basura para lograr objetivos específicos de riesgo y ganancias. Mientras que programas de hojas de cálculo y C/C++ continúan siendo útiles, los lenguajes simbólicos de programación —por ejemplo, lenguajes que manipulan tanto los números como los símbolos que representan las estructuras financieras— son cada vez más necesarios para afrontar la creciente complejidad del mundo de las finanzas.

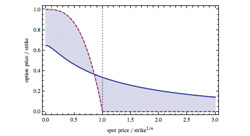
El Dr. Ross Miller,¹ uno de los primeros en aplicar un enfoque simbólico al análisis financiero, utilizó Mathematica para crear un modelo relativamente simple que es tradicionalmente numérico por naturaleza: el modelo Black-Scholes de determinación de precios de opciones.

"Mathematica permite manipular la fórmula Black-Scholes de determinación de precios directamente como una entidad simbólica. Esto simplifica grandemente la computación de varias características de una opción —una tarea tanto tediosa como proclive a errores cuando se realiza de una manera más tradicional— y hace funcionar extensiones del modelo que están hechas 'sobre la marcha'".

Mathematica entonces ayudó a continuar a partir del punto hasta donde llegó el modelo de Black-Scholes de determinación de precio de opciones. A pesar de que el modelo Black-Scholes da una solución de forma cerrada para determinar el precio de opciones europeas, los precios de muchas otras opciones no pueden establecerse con este modelo. Tales opciones incluyen las opciones norteamericanas y aquellas cuyos pagos terminales dependen de la ruta seguida por el precio de las acciones. Usando los modelos binarios y binomiales de determinación de precios de opciones y el método Monte Carlo, tres ingenieros en finanzas ² utilizaron Mathematica para determinar el precio de esas opciones.

"Sin Mathematica, otros han tenido que usar aproximaciones para fórmulas de precios para opciones, cuyos precios son difíciles de establecer. Mathematica nos permitió determinar el precio de muchas de estas opciones directamente".

1. El Dr. Ross Miller es el autor del libro Computer-Aided Financial Analysis y ha publicado muchos artículos académicos sobre transferencia de información en mercados financieros y sobre el diseño de sistemas avanzados de mercados electrónicos. Fue el jefe de investigación para el National Westminster Bank y actuó como miembro del plantel técnico del Centro de Desarrrollo e Investigación Corporativa de General Electric antes de abrir su propia compañía consultora especializada en administración de inversiones y de riesgos.

2. Simon Benninga, Raz Steinmetz y John Stroughair. Dr. Benninga es el autor de Numerical Methods in Finance, y sus áreas de investigación incluyen opciones y mercados futuros. Raz Steinmetz y John Stroughair son estudiantes de postgrado en la Wharton School de la Universidad de Pennsylvania cuando se llevó a cabo esta investigación.

Historias relacionadas