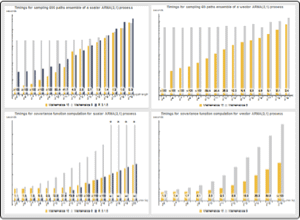
Modelo vectorial de articulaciones vs Modelo de componentes univariante
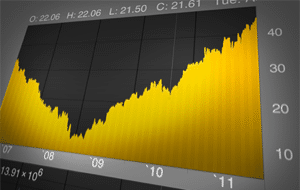
Obtenga lecturas de temperatura cada hora para mayo de 2014 en Champaign, Illinois.
| In[1]:= | X |
| In[2]:= |  X |
Utilice TimeSeriesAggregate para calcular las temperaturas máximas y mínimas diarias.
| In[3]:= | X |
Combínelos en una serie temporal vectorial.
| In[4]:= |  X |
| Out[4]= |
| Out[5]= | 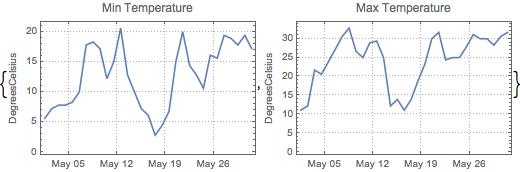 |
La primera parte de los datos será usada para encontrar un modelo, mientras que el resto de los datos servirá como un conjunto de referencia para el pronóstico.
| In[6]:= | X |
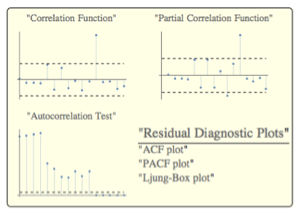
Las temperaturas presentan una correlación cruzada.
| In[7]:= | X |
| Out[7]= | 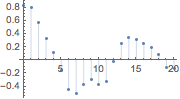 |
Encaje un modelo vectorial en los datos.
| In[8]:= | X |
| Out[8]= |
Pronostique los primeros 5 días.
| In[9]:= | X |
| Out[10]= | 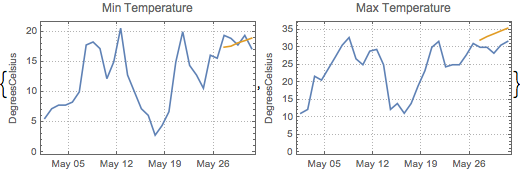 |
Encuentre modelos univariantes del mismo tipo, pero las órdenes más largas para ambas temperaturas por separado.
| In[11]:= |  X |
| Out[11]= |
| In[12]:= |  X |
| Out[12]= |
Combine pronósticos univariantes para el graficado.
| In[13]:= |  X |
| Out[13]= |
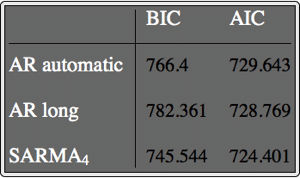
Compare los pronósticos.
| In[14]:= | X |
| Out[15]= | 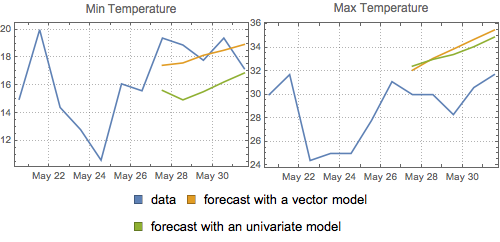 |
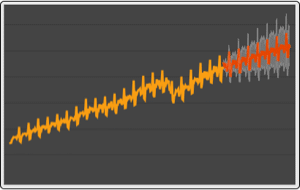
Grafique el pronóstico vectorial y las bandas de confianza del 95%.
| Out[17]= | 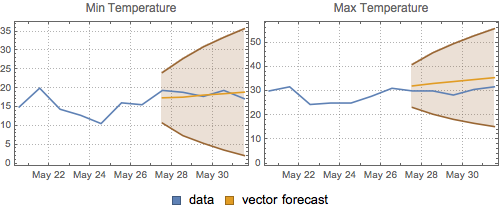 |
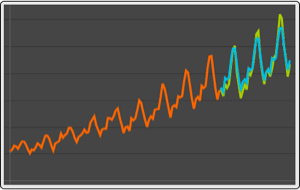
Grafique el pronóstico univariante y las bandas de confianza del 95%.
| Out[20]= | 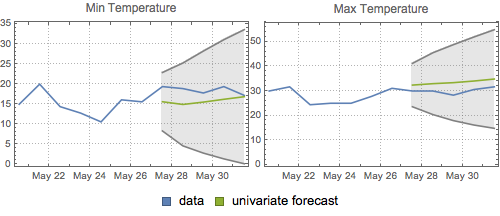 |
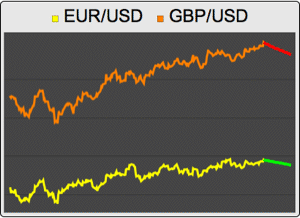
Compare ambos pronósticos y sus correspondientes bandas de confianza.
| Out[21]= | 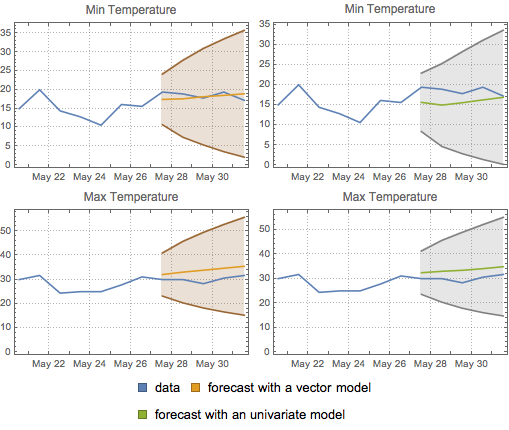 |