Core Algorithms
Compute Binormal Probability over a Polygon
Probability of standard binormal variate with 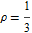 over a regular octagon of unit radius expressed in terms of Owen's T function.
over a regular octagon of unit radius expressed in terms of Owen's T function.
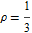 over a regular octagon of unit radius expressed in terms of Owen's T function.
over a regular octagon of unit radius expressed in terms of Owen's T function.| In[1]:= |  X |
| In[2]:= |  X |
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |