Chemical Reactions 

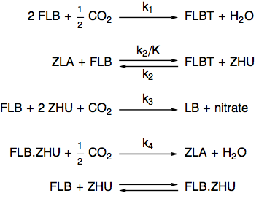
Model a chemical process of two species, FLB and ZHU, that are continuously mixed with carbon dioxide.

The inflow of carbon dioxide per unit volume is denoted as follows.

In[1]:=

X Fin = klA (pCO2/H - CO2[t]);

Specify the rate equations for each of the reactions.

In[2]:=

X r1 = k1 FLB[t]^2 CO2[t]^0.5; r2 = k2 FLBT[t] ZHU[t]; r3 = (k2/KK) FLB[t] ZLA[t]; r4 = k3 FLB[t] ZHU[t]^2 CO2[t]; r5 = k4 FLBZHU[t] CO2[t]^0.5;

The governing equations for the rate of change of concentrations of each chemical species depends on the rate equations and the reactions.

In[3]:=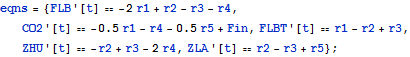

X eqns = {FLB'[t] == -2 r1 + r2 - r3 - r4, CO2'[t] == -0.5 r1 - r4 - 0.5 r5 + Fin, FLBT'[t] == r1 - r2 + r3, ZHU'[t] == -r2 + r3 - 2 r4, ZLA'[t] == r2 - r3 + r5};

The last reaction represents an equilibrium reaction.

In[4]:=

X eqEqn = Ks FLB[t] ZHU[t] == FLBZHU[t];

Define the reaction parameters for each of the reactions.

In[5]:=

X params = {k1 -> 18.7, k2 -> 0.58, k3 -> 0.09, k4 -> 0.42, KK -> 34.4, klA -> 3.3, Ks -> 115.83, pCO2 -> 0.9, H -> 737};

Specify the initial concentrations of each species.

In[6]:=

X ics = {FLB[0] == 0.444, CO2[0] == 0.00123, FLBT[0] == 0, ZHU[0] == 0.007, ZLA[0] == 0};

Solve and visualize the change in concentration of the species over time.

In[7]:=

X sol = NDSolve[{eqns, eqEqn, ics} /. params, {FLB, ZHU, , CO2, ZLA}, {t, 0, 200}];

In[8]:=

X Row[Plot[Evaluate[#[t] /. sol], {t, 0, 200}, PlotRange -> All, PlotLabel -> #[t]] & /@ {FLB, ZHU, CO2, ZLA}]

Out[8]=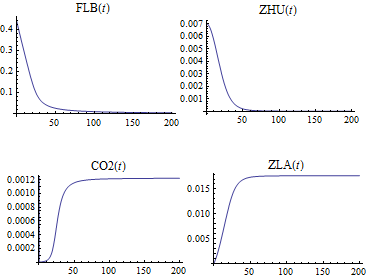