Compute Sliding Mode Solutions 

Find solutions to differential equations in 2D and 3D with discontinuities that are automatically computed using Filippov sliding mode.

Compute a solution in the plane where there is a discontinuity on the unit circle.

In[1]:=

X sxy = First[ NDSolve[{x'[t] == If[x[t]^2 + y[t]^2 > 2, 1, x[t]], y'[t] == If[x[t]^2 + y[t]^2 > 2, -1, y[t]], x[0] == -1/15, y[0] == 1/10}, {x, y}, {t, 0, 10}]]; pplot = ParametricPlot[Evaluate[{x[t], y[t]} /. sxy], {t, 0, 10}, PlotStyle -> {Thickness[0.01], Red}, PlotRange -> {{-2, 2}, {-2, 2}}, Prolog -> {GrayLevel[.9], Disk[{0, 0}, Sqrt[2]]}, AxesLabel -> {"x", "y"}]

Out[1]=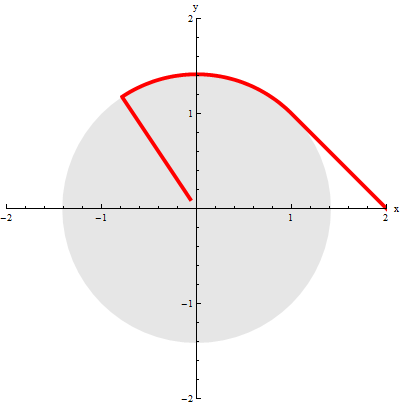

When the solution first reaches the circle, the vector field on both sides points towards the discontinuity, leading to sliding mode along the circle until the vector field on the outside no longer points inward.

In[2]:=

X Show[pplot, vf = VectorPlot[ If[x^2 + y^2 > 2, {1, -1}, {x, y}], {x, -2, 2}, {y, -2, 2}, VectorStyle -> Gray, VectorPoints -> 30, VectorScale -> {.02, 1, None}]]

Out[2]=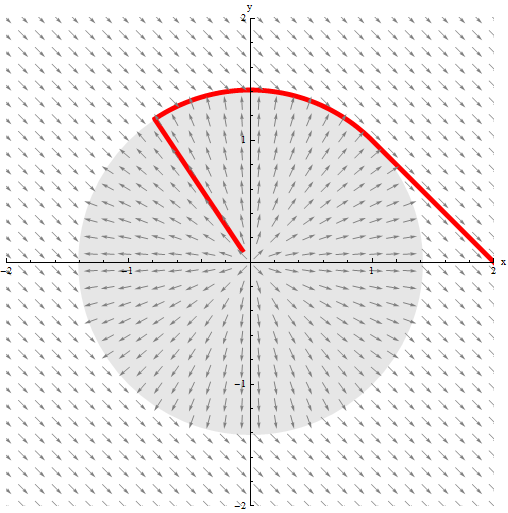

Compute multiple solutions.

In[3]:=

X solutions = Table[First[ NDSolve[{x'[t] == If[x[t]^2 + y[t]^2 > 2, 1, x[t]], y'[t] == If[x[t]^2 + y[t]^2 > 2, -1, y[t]], x[0] == Cos[\[Theta]]/4, y[0] == Sin[\[Theta]]/4}, {x, y}, {t, 0, 10}]], {\[Theta], 0, 2 \[Pi], .1}]; Show[ParametricPlot[Evaluate[{x[t], y[t]} /. solutions], {t, 0, 10}, PlotStyle -> Thickness[.01], PlotRange -> {{-2, 2}, {-2, 2}}, Prolog -> {GrayLevel[.9], Disk[{0, 0}, Sqrt[2]]}, AxesLabel -> {"x", "y"}], vf]

Out[3]=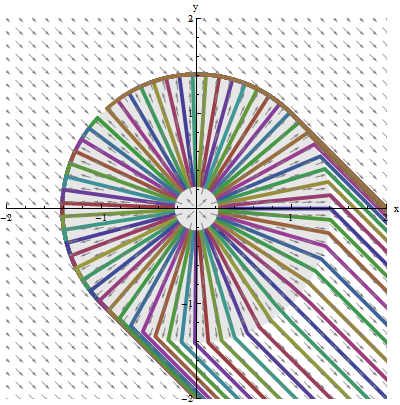

In higher dimensions, sliding mode is possible on more than one discontinuity surface at once. This happens for two discontinuity surfaces in 3D defined by the surface of a sphere 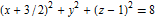and the plane 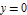, with the vector field given by .

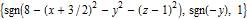In[4]:=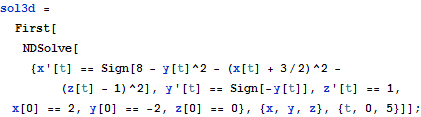

X sol3d = First[ NDSolve[{x'[t] == Sign[8 - y[t]^2 - (x[t] + 3/2)^2 - (z[t] - 1)^2], y'[t] == Sign[-y[t]], z'[t] == 1, x[0] == 2, y[0] == -2, z[0] == 0}, {x, y, z}, {t, 0, 5}]];

Make a plot by forming contour surfaces for the discontinuities and using ParametricPlot3D for the solution curve.

In[5]:=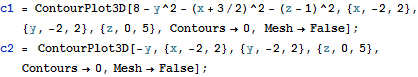

X c1 = ContourPlot3D[ 8 - y^2 - (x + 3/2)^2 - (z - 1)^2, {x, -2, 2}, {y, -2, 2}, {z, 0, 5}, Contours -> 0, Mesh -> False]; c2 = ContourPlot3D[-y, {x, -2, 2}, {y, -2, 2}, {z, 0, 5}, Contours -> 0, Mesh -> False];

In[6]:=

X p1 = ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. sol], {t, 0, 5}, PlotStyle -> {Thickness[.015], Red}]; Show[c1, c2, p1, ImageSize -> Medium]

Out[6]=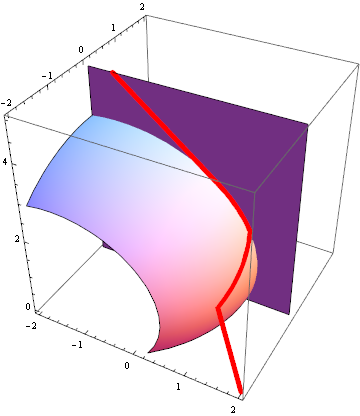