Hybrid Dynamical Systems 

In[2]:=

X GraphicsGrid[{Map[ ParametricPlot[{Subscript[x, 1][t], Subscript[x, 2][t]} /. sol, {t, 0, #}, PlotPoints -> 500, PlotRange -> {{-1, 2.5}, {-2, 1.5}}] &, {10, 50, 150}]}]

In[5]:=

X GraphicsGrid[{Map[ ParametricPlot[{Subscript[x, 1][t], Subscript[x, 2][t]} /. sol1, {t, 0, #}, PlotPoints -> 500, PlotRange -> {{-3, 3}, {-3, 3}}] &, {10, 50, 150}], Map[ParametricPlot[{Subscript[x, 1][t], Subscript[x, 2][t]} /. sol2, {t, 0, #}, PlotPoints -> 500, PlotRange -> {{-3, 3}, {-3, 3}}, PlotStyle -> Black] &, {10, 50, 150}], Map[ ParametricPlot[{Subscript[x, 1][t], Subscript[x, 2][t]} /. sol3, {t, 0, #}, PlotPoints -> 500, PlotRange -> {{-3, 3}, {-3, 3}}, PlotStyle -> Red] &, {10, 50, 150}]}]

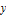Each time the solution crosses the negative axis, reflect it across the axis.

In[1]:=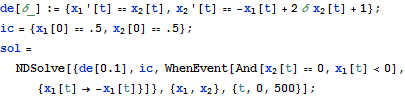

X de[\[Delta]_] := {Subscript[x, 1]'[t] == Subscript[x, 2][t], Subscript[x, 2]'[t] == -Subscript[x, 1][t] + 2 \[Delta] Subscript[x, 2][t] + 1}; ic = {Subscript[x, 1][0] == .5, Subscript[x, 2][0] == .5}; sol = NDSolve[{de[0.1], ic, WhenEvent[ And[Subscript[x, 2][t] == 0, Subscript[x, 1][t] < 0], {Subscript[x, 1][t] -> -Subscript[x, 1][t]}]}, {Subscript[ x, 1], Subscript[x, 2]}, {t, 0, 500}];

Out[2]=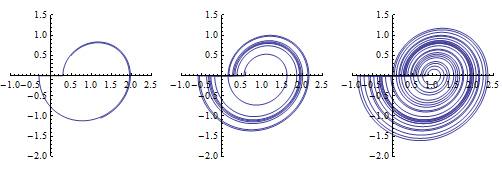

Compare the solutions for several different values of .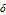

In[3]:=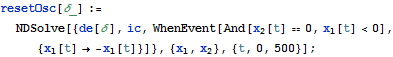

X resetOsc[\[Delta]_] := NDSolve[{de[\[Delta]], ic, WhenEvent[ And[Subscript[x, 2][t] == 0, Subscript[x, 1][t] < 0], {Subscript[x, 1][t] -> -Subscript[x, 1][t]}]}, {Subscript[ x, 1], Subscript[x, 2]}, {t, 0, 500}];

In[4]:=

X {sol1, sol2, sol3} = Map[resetOsc, {.1, .15, .2}];

Out[5]=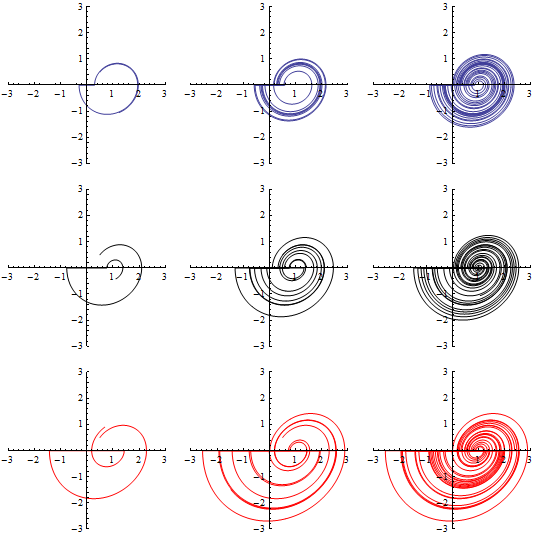