Proportional-Derivative Controller
Model the position of a moving body with 1 kg mass and use a sampled proportional-derivative (PD) controller to keep the position at a constant reference value.
 |
| In[1]:= | 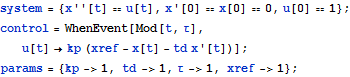 X |
| In[2]:= | X |
| In[3]:= | X |
| Out[3]= | 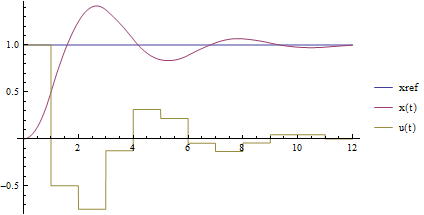 |
| « View all new features in Mathematica 9 | ◄ previous | next ► |
 |
| In[1]:= | 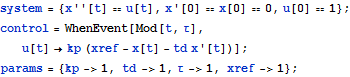 X |
| In[2]:= | X |
| In[3]:= | X |
| Out[3]= |  |