Built-in Symbolic Tensors

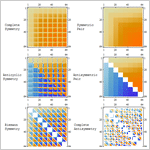
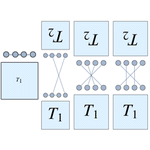
Mathematica 9 introduces support for symbolic array objects, from simple vectors to arrays of any rank, dimensions, and symmetry. New tensor algebra operations allow the construction of polynomials of symbolic arrays. These can be simplified into a standard form using efficient algorithms and used to derive or prove symbolic identities. A new type of structured array stores only symmetry and independent components. This can lead to substantial memory saving, most significantly in the case of antisymmetry. New differential operators for vector analysis can handle explicit arrays of any type and rank and interpret them in various orthogonal coordinate systems.