Fundamentals of Queueing Theory 

Verify Little's law 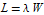relating the system size and waiting time for a queue.

In[1]:=

X \[ScriptCapitalQ] = QueueingProcess[\[Lambda], \[Mu]];

In[2]:=

X QueueProperties[\[ScriptCapitalQ] , "QueueDiagram"]

Out[2]=

In[3]:=

X L = QueueProperties[\[ScriptCapitalQ], "MeanSystemSize"]

Out[3]=

In[4]:=

X W = QueueProperties[\[ScriptCapitalQ], "MeanSystemTime"]

Out[4]=

In[5]:=

X L == \[Lambda] W

Out[5]=

Verify Burke's theorem for a feedforward network with three queues in series.

In[6]:=

X \[ScriptCapitalN] = QueueingNetworkProcess[\!\(\* TagBox[ RowBox[{"(", "", TagBox[GridBox[{ {"3."}, {"0"}, {"0"} }, GridBoxAlignment->{ "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.5599999999999999]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], Column], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"0", "1", "0"}, {"0", "0", "1"}, {"0", "0", "0"} }, GridBoxAlignment->{ "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), \!\(\* TagBox[ RowBox[{"(", "", TagBox[GridBox[{ {"4"}, {"7"}, {"8.2"} }, GridBoxAlignment->{ "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.5599999999999999]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], Column], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), \!\(\* TagBox[ RowBox[{"(", "", TagBox[GridBox[{ {"1"}, {"1"}, {"1"} }, GridBoxAlignment->{ "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.5599999999999999]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], Column], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)];

Compute a probability for the steady state of the network.

In[7]:=

X Probability[ x == 2 && y == 1 && z == 3, {x, y, z} \[Distributed] \[ScriptCapitalN][\[Infinity]]]

Out[7]=

Verify the result using Burke's theorem.

In[8]:=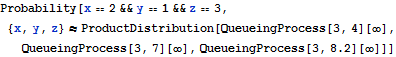

X Probability[ x == 2 && y == 1 && z == 3, {x, y, z} \[Distributed] ProductDistribution[QueueingProcess[3, 4][\[Infinity]], QueueingProcess[3, 7][\[Infinity]], QueueingProcess[3, 8.2][\[Infinity]]]]

Out[8]=

Verify the definition of the Erlang B loss probability for an M/M/c/c queue.

In[9]:=

X Probability[n == c, Distributed[n, StationaryDistribution[QueueingProcess[\[Lambda], \[Mu], c, c]]], Assumptions -> Element[c, Integers] && c > 0]

Out[9]=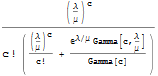

Use the built-in ErlangB function to compute the same result.

In[10]:=

X ErlangB[c, \[Lambda]/\[Mu]]

Out[10]=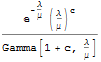

Confirm that the two answers are indeed the same.

In[11]:=

X Probability[n == c, Distributed[n, StationaryDistribution[QueueingProcess[\[Lambda], \[Mu], c, c]]], Assumptions -> Element[c, Integers] && c > 0]; ErlangB[c, \[Lambda]/\[Mu]]; FullSimplify[% - %%]

Out[11]=