Parameter Sweeps
Model a bouncing ball dropped from 20 different heights.
| In[2]:= | X |
| In[5]:= |  X |
| In[1]:= | 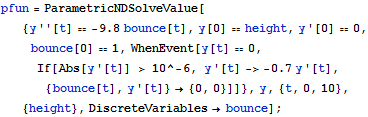 X |
| Out[2]= | 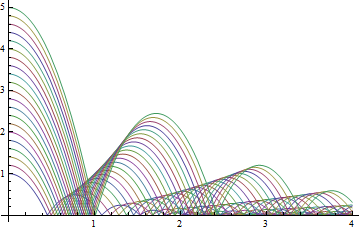 |
Find a height such that the ball will land at time t=2.5.
| In[3]:= | 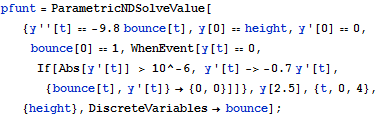 X |
| In[4]:= | X |
| Out[4]= |
| Out[5]= | 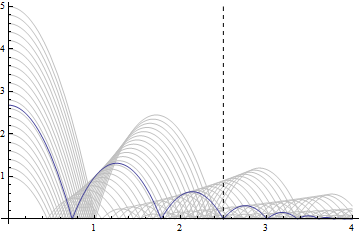 |
| « View all new features in Mathematica 9 | ◄ previous | next ► |
| In[2]:= | X |
| In[5]:= |  X |
| In[1]:= | 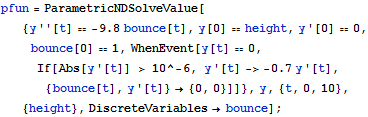 X |
| Out[2]= |  |
| In[3]:= | 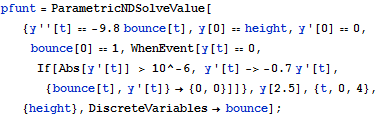 X |
| In[4]:= | X |
| Out[4]= |
| Out[5]= |  |