Sensitivity of the Lorenz Equations 

Visualize the sensitivity of the Lorenz equations with respect to a parameter.

In[1]:=

X leqns = {Derivative[1][x][t] == -3 (x[t] - y[t]), Derivative[1][y][t] == -x[t] z[t] + \[Sigma] x[t] - y[t], Derivative[1][z][t] == x[t] y[t] - z[t]};

In[2]:=

X pl = ParametricNDSolveValue[{leqns, x[0] == z[0] == 0, y[0] == 1}, Function[Evaluate[{x[#], y[#], z[#]}]], {t, 0, 15}, \[Sigma]];

A plot of the solution shows a part of the classic Lorenz attractor. The color changes from red to blue as time increases.

In[3]:=

X ParametricPlot3D[pl[28][t], {t, 0, 15}, ColorFunction -> (Hue[.8 #4] &)]

Out[3]=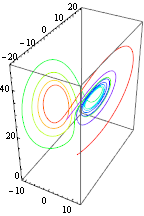

The derivative with respect to 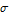shows how sensitive the solution is to changes in 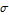. The colors correspond to the same time values as in the plot above.

In[4]:=

X ParametricPlot3D[pl'[28][t], {t, 0, 15}, PlotRange -> All, ColorFunction -> (Hue[.8 #4] &)]

Out[4]=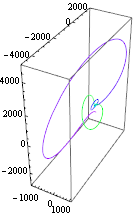

Two solutions with nearby 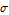deviate quickly. The large sensitivity is an indication that this is likely.

In[5]:=

X ParametricPlot3D[{pl[28][t], pl[28.1][t], pl[27.9][t]}, {t, 0, 15}, PlotRange -> All, PlotStyle -> {Blue, Red, Green}]

Out[5]=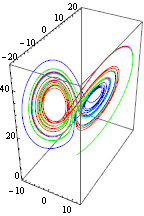

Another way to see the sensitivities is to consider a coordinate basis local to a point on the trajectory, so that one coordinate points along the trajectory and two are orthogonal. The orthogonal directions are chosen so that one component is in the direction of the nearest equilibrium point, since around these points the trajectory stays near a plane.

In[6]:=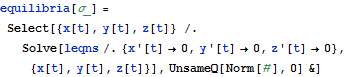

X equilibria[\[Sigma]_] = Select[{x[t], y[t], z[t]} /. Solve[leqns /. {x'[t] -> 0, y'[t] -> 0, z'[t] -> 0}, {x[t], y[t], z[t]}], UnsameQ[Norm[#], 0] &]

Out[6]=

In[7]:=

X sb[\[Sigma]_][t_?NumberQ] := Module[{v, eqv, o}, v = pl[\[Sigma]]; eqv = First[Nearest[Map[v[t] - # &, equilibria[\[Sigma]]], v[t], 1]]; o = Orthogonalize[{v'[t], eqv, Cross[v'[t], eqv]}]; o.pl'[\[Sigma]][t]]

In[8]:=

X ParametricPlot3D[sb[28][t], {t, 0, 15}, PlotRange -> All, ColorFunction -> (Hue[.8 #4] &), PlotRange -> All, BoxRatios -> 1, AxesLabel -> {"p", "o1", "o2"}]

Out[8]=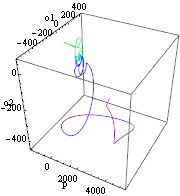

The largest part of the sensitivity is in the direction along the trajectory.

Using the decomposition of the sensitivity above, a plot can be made that shows the scaled magnitude of the sensitivity in the directions orthogonal to the trajectory.

In[9]:=

X Block[{\[Sigma] = 28}, ParametricPlot3D[ pl[\[Sigma]][ t] + .025 Abs[sb[\[Sigma]][t]] {0, Cos[\[Theta]], Sin[\[Theta]]}, {t, 0, 15}, {\[Theta], 0, 2 \[Pi]}, PlotPoints -> {300, 20}, Mesh -> None, PlotStyle -> Opacity[.4], BoxRatios -> 1, PlotRange -> All, ImageSize -> Medium, AxesLabel -> {"x"."y", "z"}]]

Out[9]=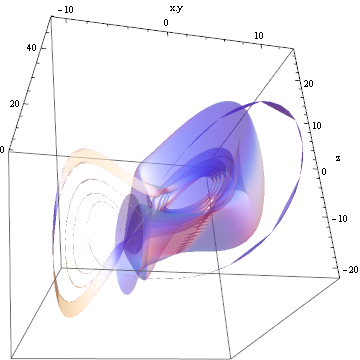