New in Mathematica 9 › Social Network Analysis

Statistical Analysis of the Slashdot Social Network

Use Mathematica's strong probability and statistical capabilities to analyze the social network emerging from Slashdot, a technology-related news website known for its specific user community.

In[1]:=

In[2]:=

distPlot[emdist_, lndist_, pdist_] :=
 Block[{pstyle = {Red, Directive[Thick, Darker[Blue]], 
     Directive[Thick, Darker[Green], Dashing[{Medium, Small}]] }, 
   plots, listplot},
  plots = 
   LogLinearPlot[{CDF[lndist, x], CDF[pdist, x]} // Evaluate, {x, 5, 
     1500}, PlotStyle -> pstyle[[2 ;;]]];
  listplot = 
   ListLogLinearPlot[{Table[{x, CDF[emdist, x]}, {x, 
       DistributionDomain[emdist]}]}, PlotRange -> All, 
    PlotMarkers -> {Graphics[{pstyle[[1]], Circle[{0, 0}, 1]}], 0.03}];
  Legended[
   Show[{plots, listplot}, ImageSize -> 400, Frame -> True, 
    GridLinesStyle -> Directive[GrayLevel[.8]], 
    GridLines -> Automatic], 
   Placed[SwatchLegend[pstyle, {"data", "log-normal", "pareto"}, 
     LegendMarkers -> {Graphics[{Red, Circle[{0, 0}, 1]}], 
       Graphics[{Line[{{0, 0}, {2, 0}}]}], 
       Graphics[{Line[{{0, 0}, {2, 0}}]}]}, 
     LegendMarkerSize -> {8, {20, 10}, {20, 10}}, 
     LegendFunction -> "Frame", 
     Background -> White], {{.98, .03}, {1, 0}}]]
  ]

Import the data and build the friend/foe network.

In[3]:=

In[4]:=

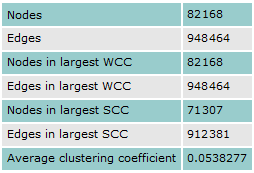
Find the basic statistics.

In[5]:=

Out[5]//TraditionalForm=

Analyze the in-degree distribution.

In[6]:=

In[7]:=

Out[7]=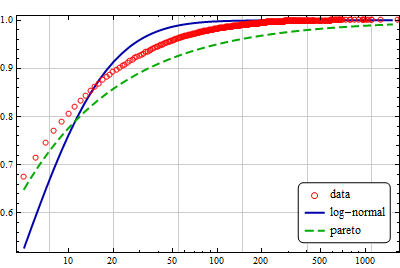