Heston Model
| In[5]:= |  X |
Define an ItoProcess corresponding to the correlated 2D Wiener process.
| In[1]:= | X |
Define a Heston model by SDEs driven by the correlated 2D Wiener process.
| In[2]:= |  X |
Simulate the model using a stochastic Runge-Kutta scheme.
| In[3]:= |  X |
Visualize the sample paths.
| In[4]:= |  X |
| Out[4]= | 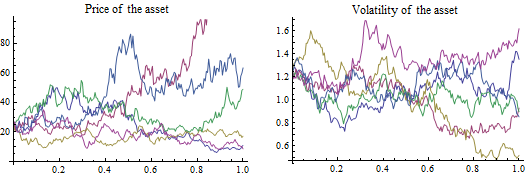 |