| More about Mathematica » |
Building on two decades of leadership in special functions, Mathematica 7 adds several major new categories of special functions, particularly ones of importance in modern combinatorics and number theory. Many of the functions have been studied extensively in the theoretical literature, but Mathematica 7 for the first time makes them computable in practice--allowing a host of new applications and experiments.
- Comprehensive symbolic and numeric treatment of over 40 new special functions.
- Full support for q-functions and basic hypergeometric series. »
- Support for explicit evaluation of Dirichlet L-functions. »
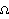 (n),
(n), 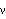 (n), Mangoldt lambda, etc. functions for counting factors of integers. »
(n), Mangoldt lambda, etc. functions for counting factors of integers. »- Riemann R prime-counting function. »
- Prime zeta function. »
- Hyperfactorial and Barnes G-generalizations of factorials. »
- Anger and Weber inhomogeneous Bessel-like functions. »
- Specialized trigonometric and hyperbolic functions (Gudermannian, haversine, etc.) »
- Champernowne numbers. »
- Full integration of special functions into sums, integrals, equation solving, etc.