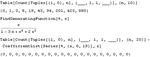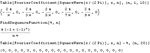| More about Mathematica » |
Mathematica 7 introduces a new level of systematic integer sequence analysis, including sequence generation, transforms and sequence recognition. Recent algorithmic advances at Wolfram Research for the first time make it possible to take lists of sequence elements and systematically find large classes of closed-form Mathematica formulas for them—allowing robust integer sequence recognition to become a routine part of programmatic discovery in experimental mathematics.
- Systematic recognition of closed forms from lists of integer sequence terms. »
- Recognition of general holonomic sequences with a variety of transformations.
- Reconstruction of sequence term functions, given as Mathematica pure functions.
- Reconstruction of symbolic generating functions. »
- Algorithmic coverage of a large fraction of sequences that occur in practice from OEIS and other databases.
- Highly efficient linear recurrence generation and recognition. »
- Systematic recognition of sequences from linear recurrences with polynomial coefficients. »
- Efficient iterative solvers for ordinary and partial difference equations, and difference-algebraic equations. »
- Symbolic computation of generating functions from sequence term formulas.
- Symbolic computation of the nth term in series. »
- Multivariate generating functions and sequence formulas. »
- Dirichlet transform and convolution. »
- Integer sequence analysis for both numerical and symbolic data elements.
- Full integration with Mathematica discrete and continuous calculus functionalities.