Wolfram Archive
Wolfram Programming Lab is a legacy product.
All the same functionality and features, including access to Programming Lab Explorations, are available with Wolfram|One.
Start programming now. »
Explorations Home › Basic › Heart and Flower Curves Static Preview
Try it now »
(no sign-in required)

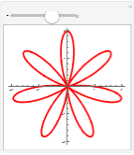
Heart and Flower Curves

Use polar plots to make natural-looking shapes.

Run the code to make a heart-like (“cardioid”) plot. Try values other than 0.5—for example, 1 or 4:

SHOW/HIDE DETAILS

PolarPlot plots curves in polar coordinates.

This plots the path of a point that has a constant distance of 1 unit from the origin as an angle sweeps from 0 to 360 degrees:

PolarPlot[1, {angle, 0 Degree, 360 Degree}]

Drag the slider to see how the curve is plotted:

This plots the path of a point whose distance from the origin is proportional to the angle:

PolarPlot[angle, {angle, 0 Degree, 360 Degree}]

Drag the slider to see how this curve is plotted:

This plots a heart shape (“cardioid”):

PolarPlot[1 - Sin[0.5 angle], {angle, 0 Degree, 360 Degree}]

Drag the slider to see how the cardioid is plotted:

HIDE DETAILS
PolarPlot[1 - Sin[0.5 angle], {angle, 0 Degree, 360 Degree}]

Allow the parameter to change. Drag the slider to get different shapes:
 

Hint: press (Windows) or (Mac) while dragging the slider for fine adjustment.


 

Note: click the “+” to the right of the slider to see the value of the parameter.

SHOW/HIDE DETAILS

Add a slider to control the value of the parameter with Manipulate.

Replace the parameter 0.5 with the variable n, wrap the PolarPlot expression with Manipulate, and specify that n varies from 0 to 10, with an initial value of 0.5. Now you can drag the slider to change the value of the parameter:

Manipulate[ PolarPlot[1 - Sin[n angle], {angle, 0 Degree, 360 Degree}], {{n, 0.5}, 0, 10} ]

Add a plot range to keep the plot from jumping around as you drag the slider:

Manipulate[ PolarPlot[1 - Sin[n angle], {angle, 0 Degree, 360 Degree}, PlotRange -> 2], {{n, 0.5}, 0, 10} ]

HIDE DETAILS
Manipulate[ PolarPlot[1 - Sin[n angle], {angle, 0 Degree, 360 Degree}, PlotRange -> 2], {{n, 0.5}, 0, 10} ]

Make the curve thick and red. Try other colors, like Blue or Green:
 

Hint: color names are capitalized—for example, Purple, Gray, and Green.

SHOW/HIDE DETAILS

PolarPlot normally draws a blue curve:

PolarPlot[1, {angle, 0 Degree, 360 Degree}]

You can change the color of the curve with PlotStyle:

PolarPlot[1, {angle, 0 Degree, 360 Degree}, PlotStyle -> Red]

Make the curve thicker with AbsoluteThickness. If there is more than one style element, put the elements in a list ({}):

PolarPlot[1, {angle, 0 Degree, 360 Degree}, PlotStyle -> {Red, AbsoluteThickness[5]}]

HIDE DETAILS
Manipulate[ PolarPlot[1 - Sin[n angle], {angle, 0 Degree, 360 Degree}, PlotRange -> 2, PlotStyle -> {Red, AbsoluteThickness[5]}], {{n, 0.5}, 0, 10}]

Share It—Make an interactive website for exploring heart and flower curves:

SHOW/HIDE DETAILS

Deploy the Manipulate to the Wolfram Cloud where anyone with a browser can use it:

CloudDeploy[ Manipulate[ PolarPlot[1 - Sin[n angle], {angle, 0 Degree, 360 Degree}, PlotRange -> 2, PlotStyle -> {Red, AbsoluteThickness[5]}], {{n, 0.5}, 0, 10}], Permissions -> "Public" ]

Click on the link in the output to visit the site.

Tell the world about your creation by sharing the link via email, tweet, or other message.

HIDE DETAILS
CloudDeploy[ Manipulate[ PolarPlot[1 - Sin[n angle], {angle, 0 Degree, 360 Degree}, PlotRange -> 2, PlotStyle -> {Red, AbsoluteThickness[5]}], {{n, 0.5}, 0, 10}], Permissions -> "Public" ]
Start programming now (no sign-in required)

Available for cloud, desktop and mobile