Solve PDEs with Complex-Valued Boundary Conditions over a Region
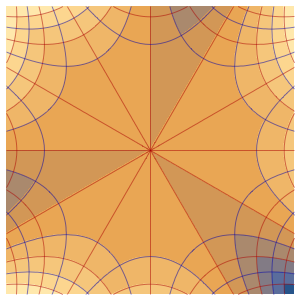
Solve a Laplace equation with a complex-valued boundary condition.
In[1]:=
ifun = NDSolveValue[{-\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) ==
1 + NeumannValue[I, x < 0],
DirichletCondition[u[x, y] == 0, x > -0]},
u, {x, y} \[Element] Disk[]]Out[1]=
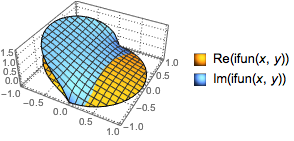
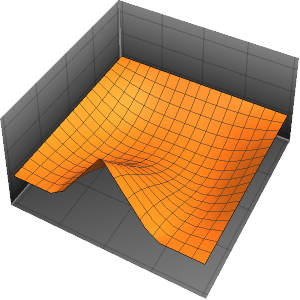
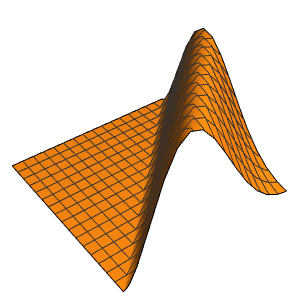
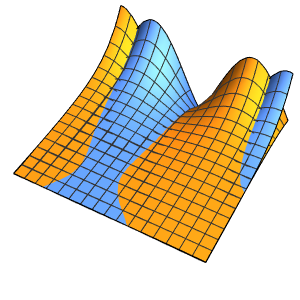
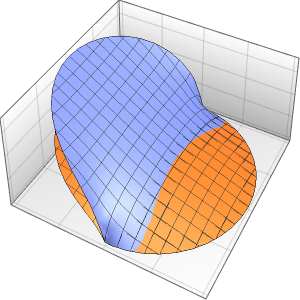
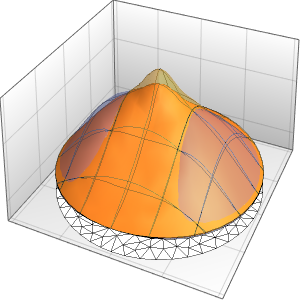
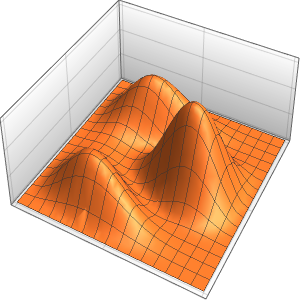
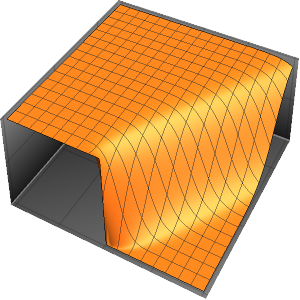
Visualize the result.
In[2]:=
Plot3D[{Re[ifun[x, y]], Im[ifun[x, y]]}, {x, y} \[Element] Disk[],
PlotTheme -> "Detailed"]Out[2]=