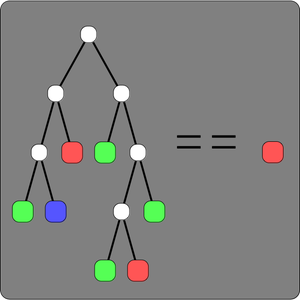
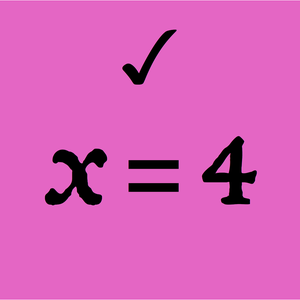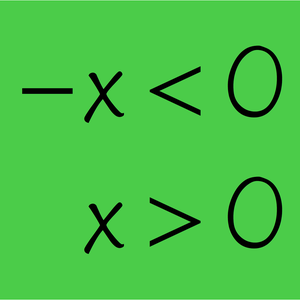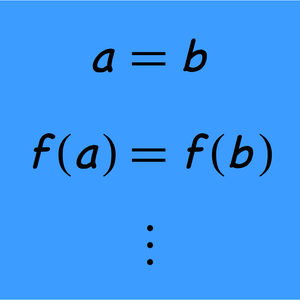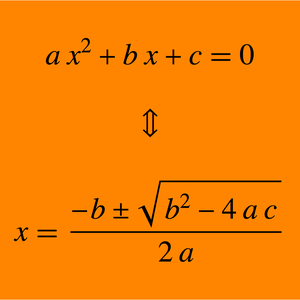- Compute the boundary, connected components and other topological properties of solution sets for real polynomial systems. »
- Express large systems naturally and succinctly using vector and matrix variables. »
- Efficiently solve large systems of equations and inequalities with special structure. »
- Solve previously intractable classes of equation and inequality systems. »
- Formulate optimization problems in a more concise and natural way using vector and matrix variables. »
- Solve new classes of exact optimization problems. »
- Solve equations "step by step" using new functions to add, multiply and otherwise combine equations and inequalities. »
- Produce automatic proofs of equational logic theorems. »
- Prove theorems using a built-in collection of axiomatic theories. »
- Present proofs in various formats, including graphs, datasets and notebooks. »
Related Examples
Related Functions
- AddSides
- ApplySides
- AxiomaticTheory
- CylindricalDecomposition
- DivideSides
- FindEquationalProof
- FindInstance
- FunctionDomain
- ModularInverse
- NegativeIntegers
- NegativeRationals
- NegativeReals
- NonNegativeIntegers
- NonNegativeRationals
- NonNegativeReals
- NonPositiveIntegers
- NonPositiveRationals
- NonPositiveReals
- Maximize
- MaxValue
- Minimize
- MinValue
- MultiplySides
- PositiveIntegers
- PositiveRationals
- PositiveReals
- PrimitivePolynomialQ
- ProofObject
- Reduce
- Root
- Solve
- SubtractSides
- VectorGreater
- VectorGreaterEqual
- VectorLess
- VectorLessEqual