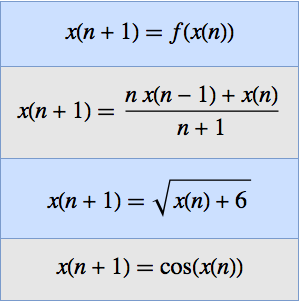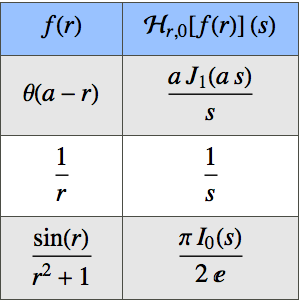Invert a Laplace Transform Using Post's Formula
Emil Post (1930) derived a formula for inverting Laplace transforms that relies on computing derivatives of symbolic order and sequence limits. Here, Post's inversion formula is implemented using the new capabilities of D and DiscreteLimit.
Post's inversion formula may be stated as follows.
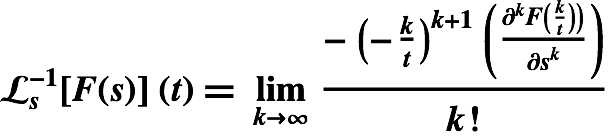
Define a function that implements Post's inversion formula.
In[1]:=1
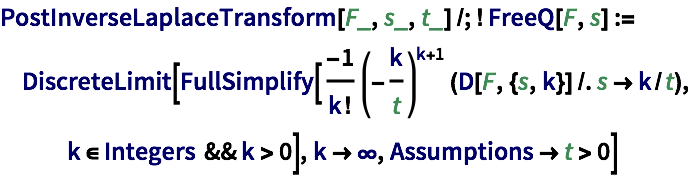
✖
Compute the inverse Laplace transform of 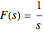 using the formula.
using the formula.
In[2]:=2
✖
Out[2]=2
Obtain the same result using InverseLaplaceTransform.
In[3]:=3
✖
Out[3]=3
Create a table of basic inverse Laplace transforms using Post's inversion formula.
show complete Wolfram Language input
Out[4]//TraditionalForm=4]//TraditionalForm=

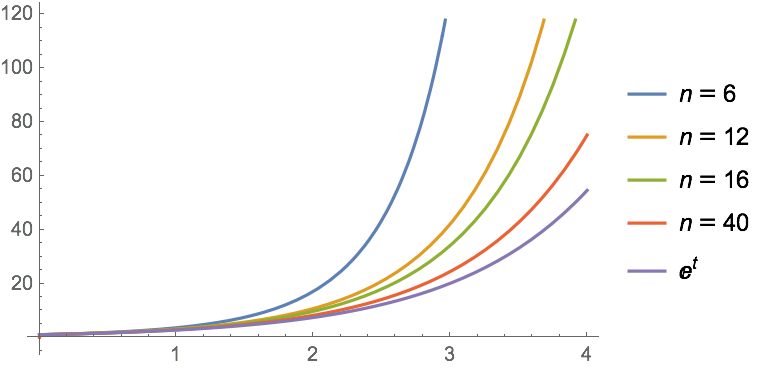
The Post formula can also be used for the numerical approximation of inverse Laplace transforms by using derivatives of sufficiently high order, as illustrated in the following.
In[5]:=5
✖
In[6]:=6
✖
In[7]:=7
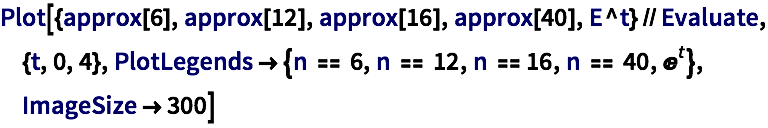
✖
Out[7]=7