Demonstrate the Avalanche Effect of a Hash Function

Hash functions play a fundamental role in modern cryptography. An important and desirable feature of a good hash function is the non-correlation of input and output, or so-called "avalanche effect", which means that a small change in the input results in a significant change in the output, making it statistically indistinguishable from random. The Hash function can produce a variety of hashes and return them in multiple formats, making it easy to study hash properties.

A hash function demonstrates the avalanche effect if a single flipped bit in the input causes a change of, on average, half the bits of the output. This example examines if the "Keccak256" Hash function has this property.

Generate a list of 10,000 random 256-bit integers.

Define a function that flips a random bit in an integer.

Create a pair of integers that differ by one bit.

Flip a random bit for each integer.

Check that the HammingDistance is exactly 1 for each pair of integers.

To do hashing on the actual bits of the integers, you need to turn each integer into a ByteArray.

Hash the byte arrays with the "Keccak256" hash.

Compute the Hamming distance for each pair of integers.

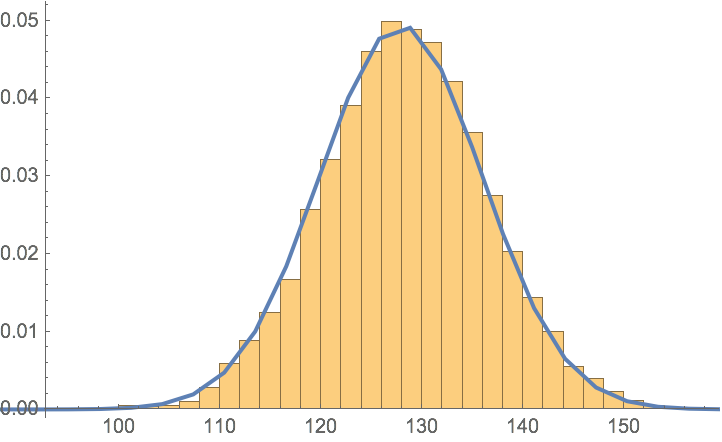
Compute the mean of the hashed Hamming distances.

Note that the mean value of 128 here is the same as if you were comparing random integer pairs, showing that the "Keccak256" scrambles its inputs very effectively.

Compute the standard deviation.

Make a histogram of the distances and the corresponding PDF of the normal distribution with the computed mean and standard deviation.