空間曲線の特性を可視化する

"SpaceCurve"実体領域では，多数の空間曲線と事前に計算された多くの特性が利用できる．

In[1]:=1

✖

Out[1]=1

In[2]:=2

✖

Out[2]=2

このコンパイルされたデータを使うと，パラメータ化された曲線に対する幾何学的特性の値を抽出してそれを可視化することが簡単にできる．Vivianiの曲線を可視化するために，まずそのパラメトリック方程式と関心のある他の特性を抽出する．

In[3]:=3

✖

Out[3]=3

以前，パラメータに依存する特性における関数スロットを表すために形式的変数（t等のように文字の下にドットが描画されたもの）を使った．特定のパラメータにおける値は以下のように代入するだけで生成される．

In[4]:=4

✖

Out[4]=4

ここでパラメトリック方程式を使ってViviani曲線をプロットし，曲線上のいくつかの点（赤い点）における法線（緑の矢印），接線（青の矢印），従法線（黄色の矢印）を描く．

In[5]:=5

✖

In[6]:=6

✖

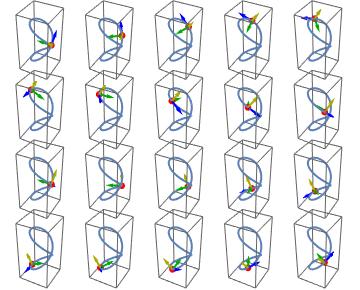
同様に，曲率等の指定された特性に基づいて曲線に簡単に色付けできる．

In[7]:=7

✖

Out[7]=7

In[8]:=8

✖

Out[8]=8

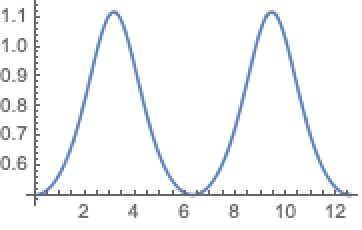
ここでは最大の曲率の領域が青でハイライトされている．

In[9]:=9

✖

Out[9]=9

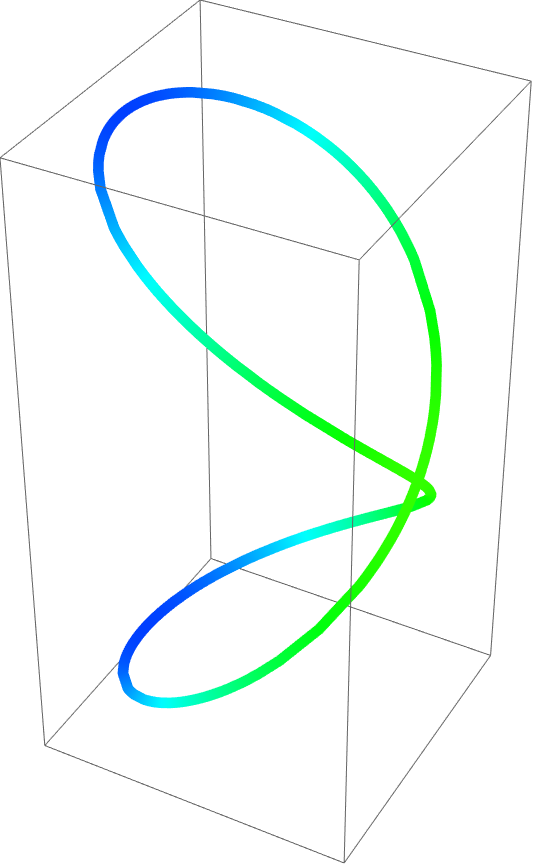
最後に，組込みの可視化関数を使うと，デカルト成分やパラメータ値等のパラメータに基づく空間曲線に簡単に色付けできる．

In[10]:=10

✖

Out[10]=10