WolframInfinitesimalrechnung und AlgebraEin Kernbestandteil der
Wolfram Language

Symbolische und numerische mathematische Berechnungen.

Für alle, von der Unterstufe bis hin zu anspruchsvollen mathematischen Forschungsprojekten. Jahrhunderte der mathematischen Entwicklung verpackt in eine Reihe außergewöhnlich leistungsfähiger Funktionen, die eng mit fortschrittlicher Visualisierung und sofort berechenbaren integrierten Daten integriert sind.

Loslegen

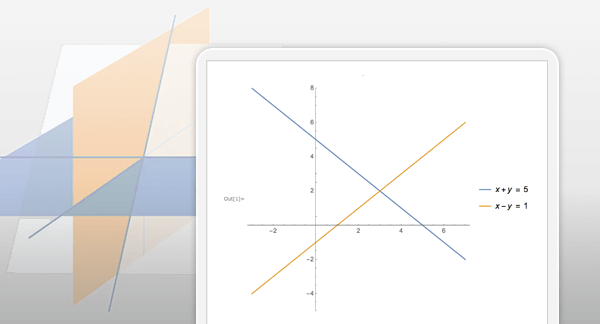
Basisalgebra und Polynomalgebra

Sie können Polynome faktorisieren und erweitern, Gleichungen und Ungleichungen manipulieren, kombinieren und vereinfachen sowie Gleichungssysteme exakt oder mit beliebiger numerischer Genauigkeit lösen. Verwenden Sie Schritt-für-Schritt-Operationen, um die Grundlagen zu beherrschen, oder verwenden Sie fortgeschrittene Algorithmen, um komplizierte Gleichungen zu lösen.

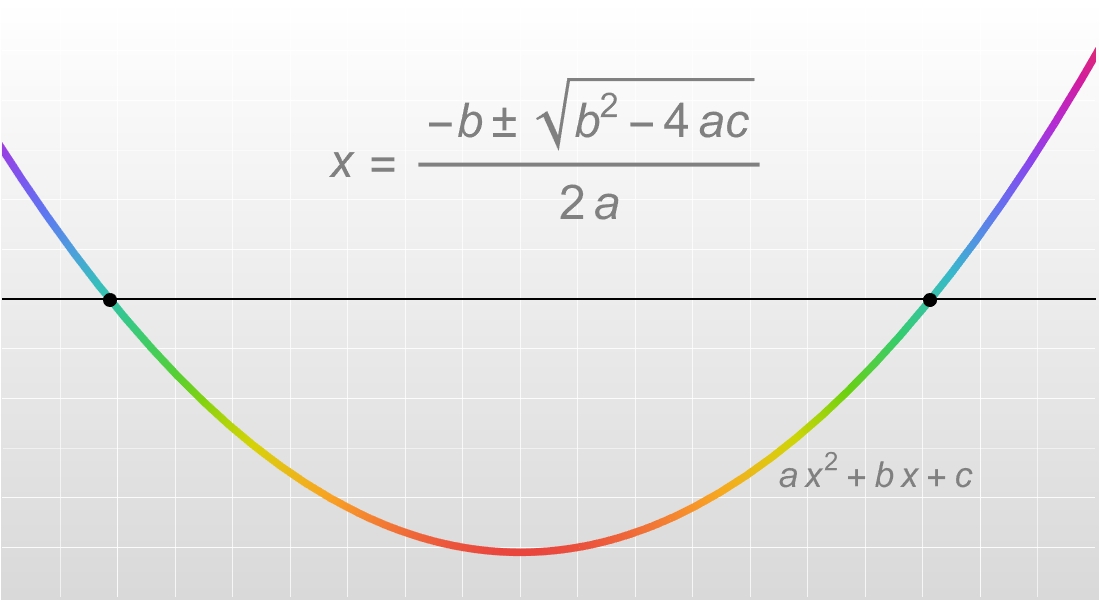
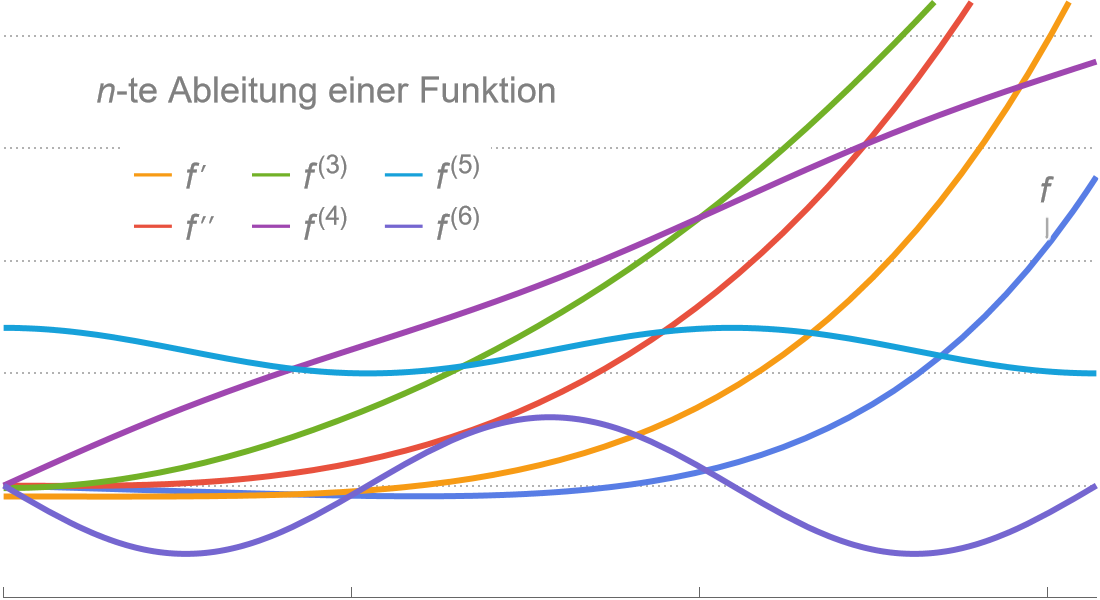
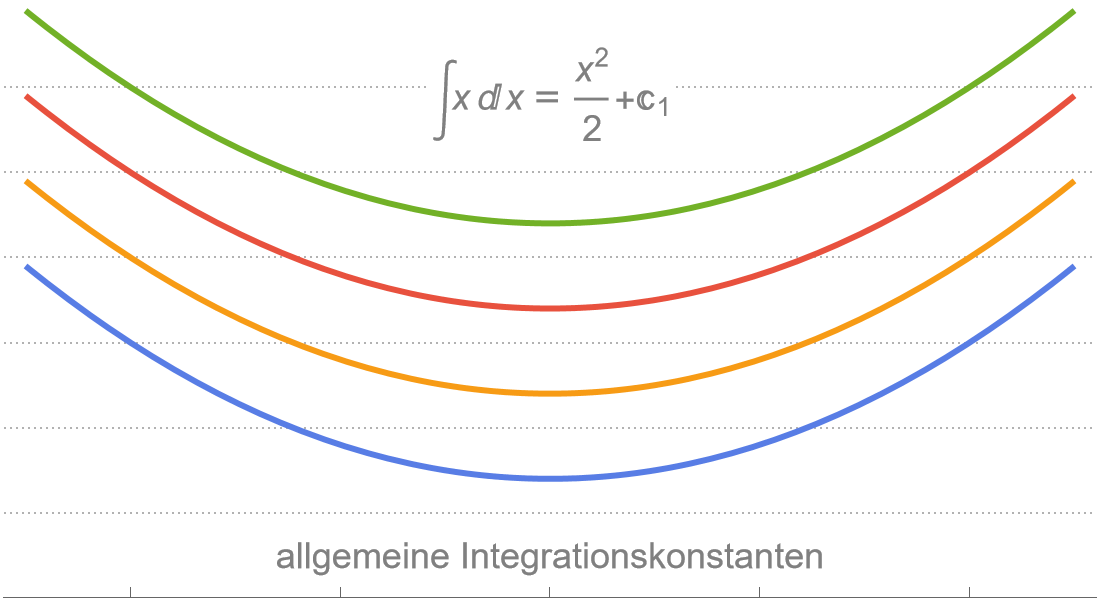
Infinitesimalrechnung

Berechnen Sie Grenzwerte, Ableitungen, Integrale und andere Konzepte der Infinitesimalrechnung mit einer Kombination aus leistungsstarken symbolischen und numerischen Methoden für optimale Ergebnisse.

Differentialgleichungen

Lösen Sie gewöhnliche, partielle, retardierte, integrale und hybride Differentialgleichungen. Differentialgleichungen sind ein wichtiges Modellierungswerkzeug für Wissenschaft und Technik. Verwenden Sie die Lösungen, um das Verhalten vorherzusagen und die Abhängigkeit von Parametern zu verstehen.

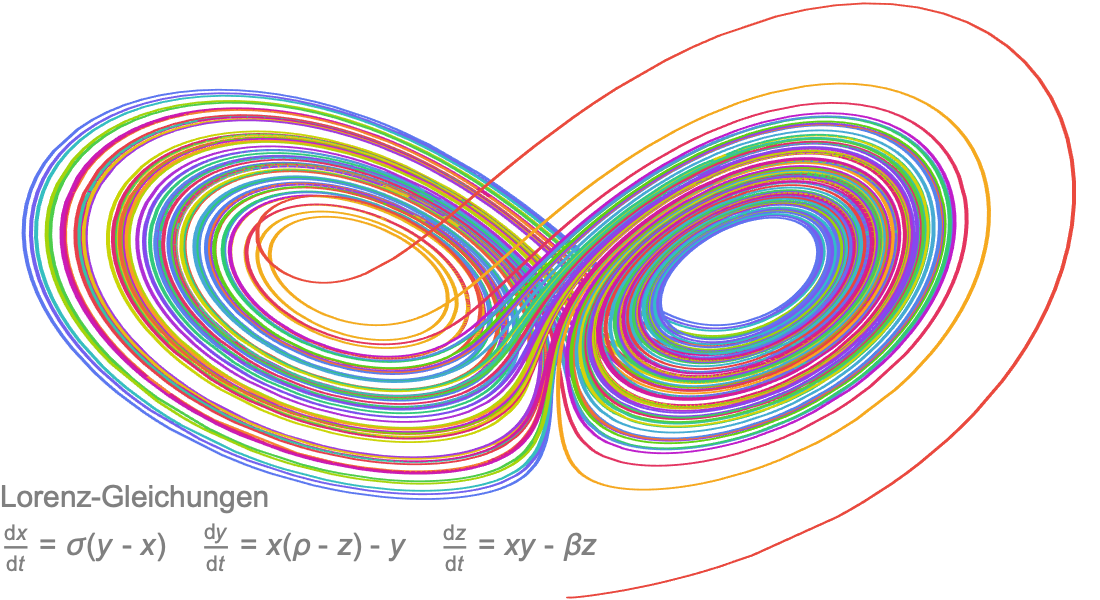
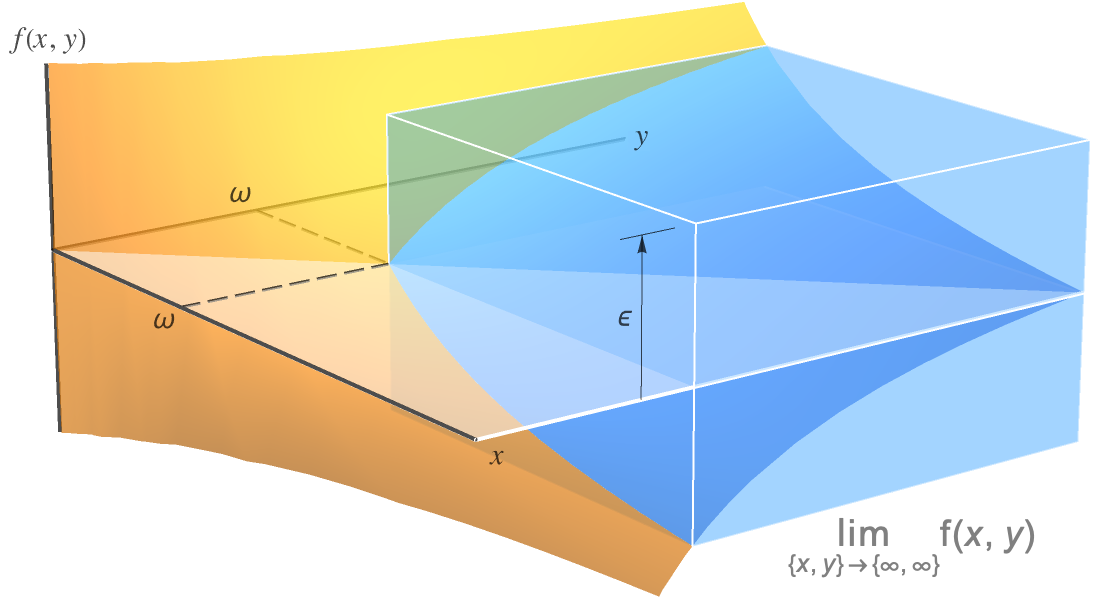
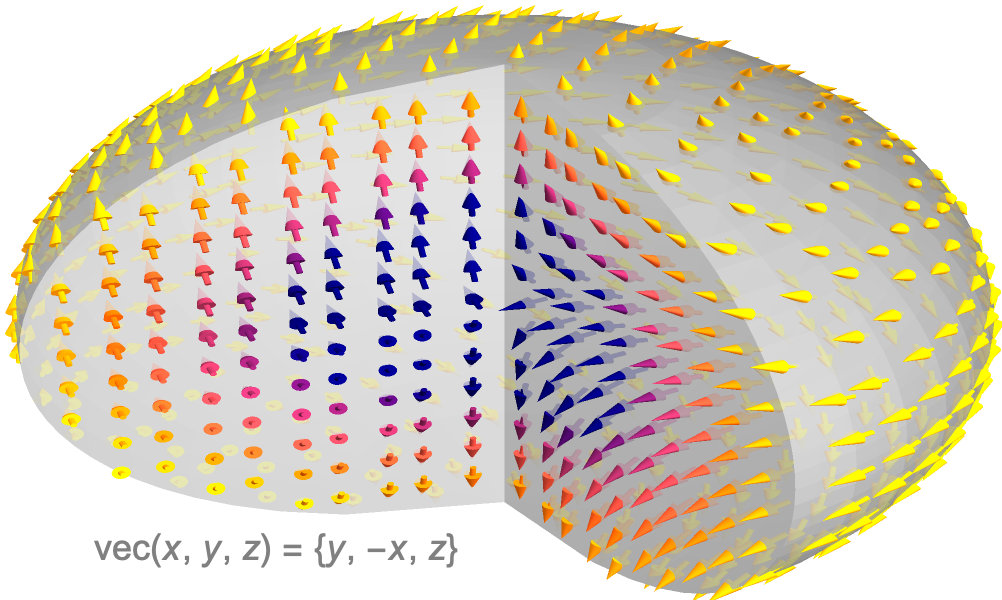
Multivariate Infinitesimalrechnung und Vektoranalyse

Arbeiten Sie mit Kernkonzepten der Geometrie, PDGs, Physik und verwandten Gebieten. Berechnen Sie auf einfache Weise mehrdimensionale Grenzwerte (skalar und vektoriell), Ableitungen (partiell, Gradient, Divergenz, etc.) und Integrale (Linie, Fläche, Volumen, etc.). Visualisieren Sie die berechneten Vektorfelder und Lösungen.

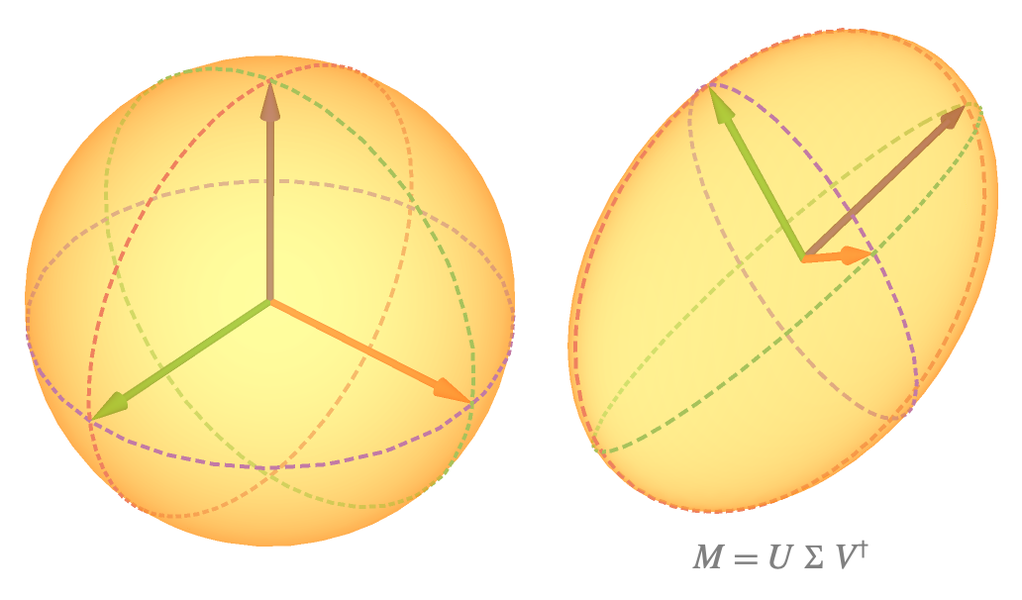
Lineare Algebra

Automatisches Lösen linearer Systeme, Berechnen von Matrix-Eigenzerlegungen und Analysieren von Daten mit SVD. Die Wolfram Language umfasst alle Funktionen der linearen Algebra, einschließlich numerischer und symbolischer vollbesetzter, dünnbesetzter und strukturierter Methoden und wird häufig in den Bereichen Datenwissenschaft, Statistik, Optimierung und Geometrie eingesetzt.

Mathematische Funktionen

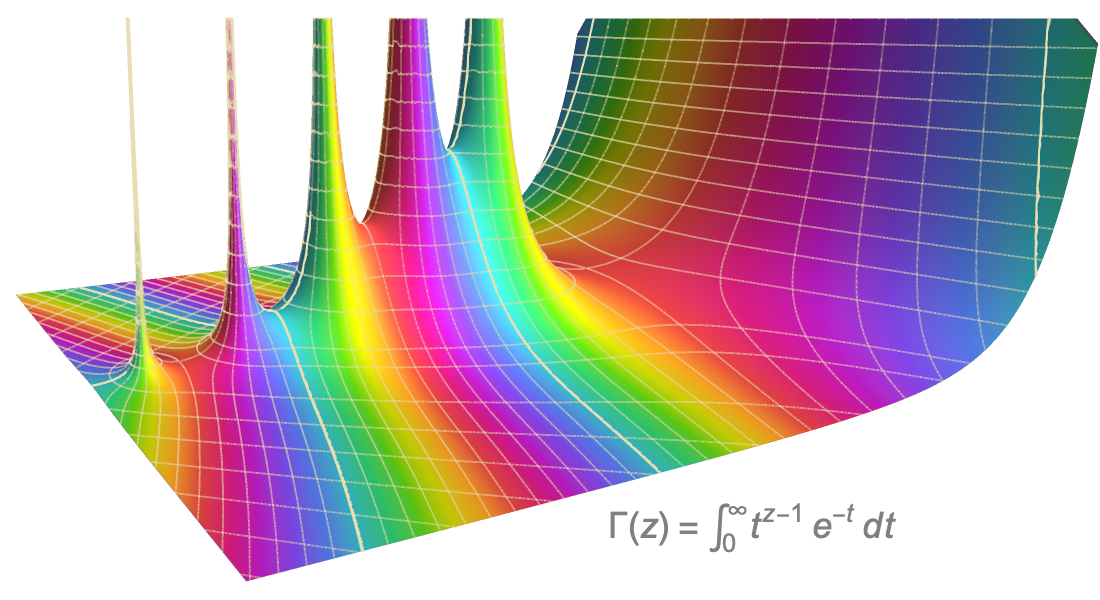
Greifen Sie auf eine umfassende Sammlung spezialisierter Funktionen aus der Physik, dem Maschinenbau, der Statistik und anderen Bereichen zu. Grundlegende, Bessel-, elliptische, hypergeometrische und andere Funktionen sind gut integriert und können visualisiert, symbolisch vereinfacht oder mit beliebiger numerischer Genauigkeit ausgewertet werden.

Diskrete Infinitesimalrechnung

Lösen Sie grundlegende Probleme der Algorithmenanalyse, numerischen Analyse und Kombinatorik, wie z. B. die Berechnung finiter und infiniter Summen und Produkte oder von Differenz- und Rekursionsgleichungen. Nutzen Sie die lückenlose Funktionssammlung, die durch moderne Methoden ergänzt wird.

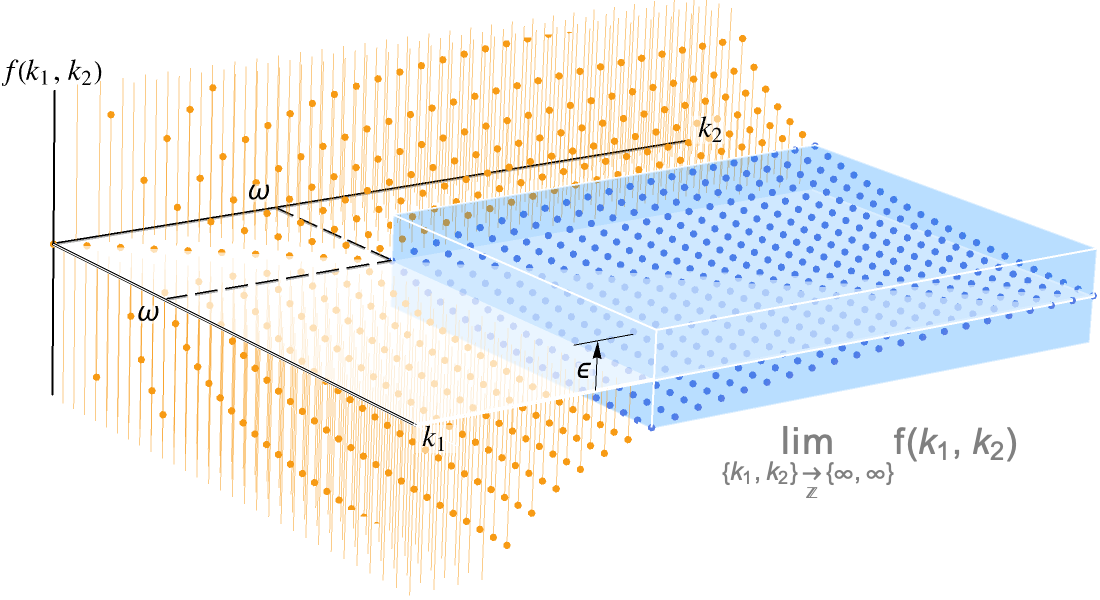
Leitfaden für die diskrete Infinitesimalrechnung

Asymptotische Analyse

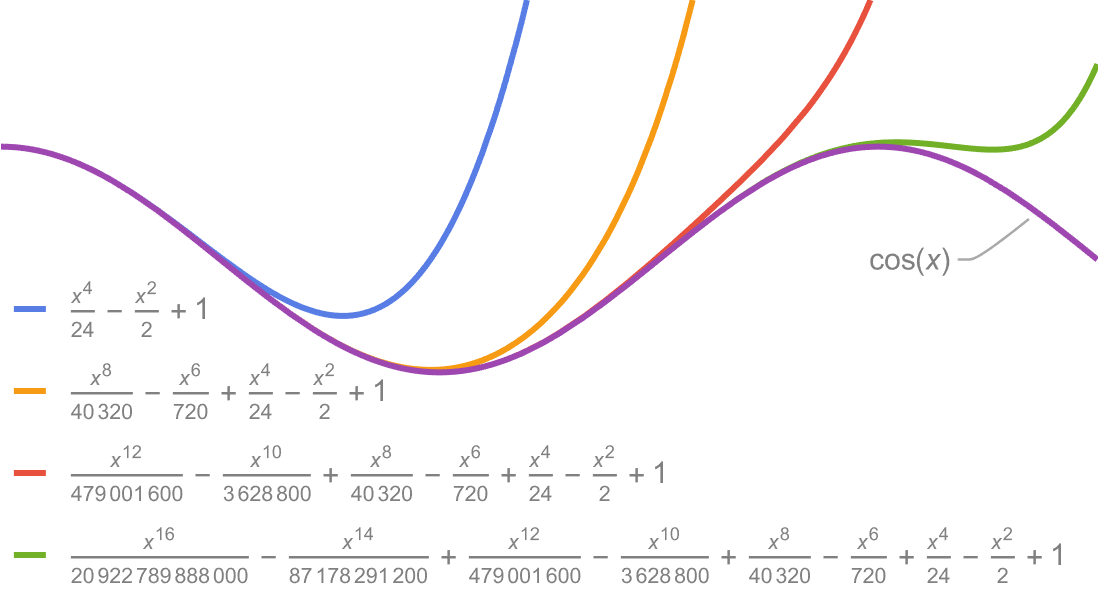
Verwenden Sie asymptotische Methoden als Ergänzung zu exakten symbolischen und numerischen Berechnungen, um Näherungslösungen für schwierige Probleme zu finden. Eine breite Auswahl automatischer Solver kann in einer Vielzahl von Bereichen eingesetzt werden, darunter Zahlentheorie, Analyse von Algorithmen, Wahrscheinlichkeit und Statistik, theoretische Physik und numerische Analyse.

Leitfaden für die asymptotische Analyse

Integral- und Summentransformierte

Transformieren Sie Daten oder Funktionen je nach Ihrem mathematischen, physikalischen oder technischen Augenmerk. Symbolische und numerische Fourier-, Laplace-, Z- und andere Transformierte wie die Hankel-, Radon- und Mellin-Transformierte sind nützlich beim Lösen von Differentialgleichungen, bei der Bildanalyse und der Merkmalserkennung in Signalen.

Live Playground

This is an interactive notebook—try making your own changes!

Continue exploring more examples:Things to Try

Dokumentation für Wolfram Infinitesimalrechnung und Algebra

Wolfram Infinitesimalrechnung und Algebra ist integrierter Bestandteil der Wolfram Language. Das vollständige System enthält über 6.000 eingebaute Funktionen, die alle Bereiche des Rechnens abdecken—alle sorgfältig integriert, damit sie perfekt zusammenarbeiten.

Wolfram Language
Vollständiger Umfang & Dokumentation

Guide

Leitfaden für die Infinitesimalrechnung

Guide

Leitfaden für mathematische Gleichungen

Overview

Monographie über Lösungswege für Differentialgleichungen

D ▪ Integrate ▪ Limit ▪ InverseFourierTransform ▪ FourierSinTransform ▪ InverseFourierSinTransform ▪ InverseFourierCosTransform ▪ FourierSeries ▪ FourierSinSeries ▪ FourierCosSeries ▪ FourierTrigSeries ▪ FourierCoefficient ▪ FourierSinCoefficient ▪ FourierCosCoefficient ▪ FourierSequenceTransform ▪ InverseFourierSequenceTransform ▪ Fourier ▪ InverseFourier ▪ FourierDST ▪ FourierDCT ▪ Spectrogram ▪ ShortTimeFourier ▪ InverseShortTimeFourier ▪ InverseSpectrogram ▪ ShortTimeFourierData ▪ SpectrogramArray ▪ Periodogram ▪ PeriodogramArray ▪ ImagePeriodogram ▪ Cepstrogram ▪ CepstrumArray ▪ CepstrogramArray ▪ TransferFunctionModel ▪ BodePlot ▪ NyquistPlot ▪ NicholsPlot ▪ SingularValuePlot ▪ CharacteristicFunction ▪ PDF ▪ PowerSpectralDensity ▪ CovarianceFunction ▪ FourierParameters ▪ DiscreteConvolve ▪ ListConvolve ▪ ImageConvolve ▪ DiscreteDelta ▪ SawtoothWave ▪ DiscreteWaveletTransform ▪ ContinuousWaveletTransform ▪ Expand ▪ Factor ▪ Reduce ▪ Coefficient ▪ Exponent ▪ Part ▪ Numerator ▪ Denominator ▪ Collect ▪ Together ▪ Apart ▪ Cancel ▪ AddSides ▪ SubtractSides ▪ MultiplySides ▪ DivideSides ▪ ApplySides ▪ PowerExpand ▪ ComplexExpand ▪ TrigExpand ▪ RootReduce ▪ ComplexityFunction ▪ Element ▪ PossibleZeroQ ▪ Refine ▪ Assuming ▪ ForAll ▪ Integers ▪ CoordinateTransformData ▪ TransformedField ▪ CoordinateTransform ▪ FromPolarCoordinates ▪ ToPolarCoordinates ▪ FromSphericalCoordinates ▪ ToSphericalCoordinates ▪ FrenetSerretSystem ▪ NLineIntegrate ▪ NSurfaceIntegrate ▪ ListVectorPlot ▪ VectorPlot3D ▪ InterpolatingFunction ▪ ParametricNDSolveValue ▪ NDSolveValue ▪ ParametricNDSolve ▪ ParametricFunction ▪ WhenEvent ▪ DirichletCondition ▪ NeumannValue ▪ PeriodicBoundaryCondition ▪ DEigenvalues ▪ DFixedPoints ▪ DStabilityConditions ▪ NBodySimulation ▪ SystemModelSimulate ▪ AccuracyGoal ▪ PrecisionGoal ▪ WorkingPrecision ▪ StepMonitor ▪ EvaluationMonitor ▪ GreenFunction ▪ CompleteIntegral ▪ Wronskian ▪ Plot ▪ StreamPlot ▪ VectorPlot ▪ FunctionSurjective ▪ FunctionBijective ▪ FunctionMonotonicity ▪ FunctionConvexity ▪ FunctionDiscontinuities ▪ FunctionPoles ▪ FunctionAnalytic ▪ FunctionMeromorphic ▪ PolynomialExpressionQ ▪ RationalExpressionQ ▪ StrictInequalities ▪ $PerformanceGoal ▪ Reals ▪ Complexes ▪ TraditionalForm ▪ UnitStep ▪ True ▪ Indeterminate ▪ Method ▪ Interval ▪ PerformanceGoal ▪ Infinity ▪ Direction ▪ FunctionContinuous ▪ AsymptoticSolve ▪ $Assumptions ▪ Automatic ▪ PrincipalValue ▪ StandardForm ▪ Root ▪ Boole ▪ ImplicitRegion ▪ RegionPlot3D ▪ Assumptions ▪ GeneratedParameters ▪ None ▪ Interpolation ▪ Variance ▪ Mean ▪ StandardDeviation ▪ FourierCosTransform ▪ MellinTransform ▪ HankelTransform ▪ Residue ▪ RegionCentroid ▪ RegionMeasure ▪ DSolveValue ▪ Simplify ▪ GenerateConditions ▪ False ▪ LineIntegrate ▪ SurfaceIntegrate ▪ ContourIntegrate ▪ Asymptotic ▪ CDF ▪ Expectation ▪ Probability ▪ MomentOfInertia ▪ ResidueSum ▪ VectorSymbol ▪ MatrixSymbol ▪ ArraySymbol ▪ NonConstants ▪ PolyGamma ▪ AiryAiPrime ▪ AiryBiPrime ▪ JacobiCD ▪ LogIntegral ▪ ExpIntegralEi ▪ SinIntegral ▪ ConditionalExpression ▪ RealAbs ▪ RealSign ▪ Ceiling ▪ Equal ▪ SymmetrizedArray ▪ SparseArray ▪ ZTransform ▪ GeneratingFunction ▪ KroneckerDelta ▪ Inactive ▪ GammaDistribution ▪ EstimatedDistribution ▪ First ▪ Outer ▪ Join ▪ Dimensions ▪ HodgeDual ▪ ArcCurvature ▪ DEigensystem ▪ DiscreteShift ▪ Solve ▪ Piecewise ▪ NDEigensystem ▪ NDEigenvalues ▪ CoefficientArrays ▪ FractionalD ▪ CaputoD ▪ Pi ▪ E ▪ Degree ▪ EulerGamma ▪ I ▪ Re ▪ Im ▪ Conjugate ▪ Arg ▪ Plus ▪ Times ▪ Power ▪ Total ▪ Abs ▪ Round ▪ Floor ▪ Min ▪ Max ▪ Clip ▪ Ramp ▪ Rescale ▪ Log ▪ Log10 ▪ Exp ▪ Sqrt ▪ Sin ▪ Cos ▪ Tan ▪ ArcTan ▪ Tanh ▪ Sinc ▪ Gamma ▪ Erf ▪ BesselJ ▪ BesselK ▪ AiryAi ▪ EllipticK ▪ LegendreP ▪ ChebyshevT ▪ HermiteH ▪ LaguerreL ▪ SpheroidalS1 ▪ JacobiSN ▪ WeierstrassP ▪ Zeta ▪ PolyLog ▪ EllipticTheta ▪ Hypergeometric2F1 ▪ HypergeometricPFQ ▪ MeijerG ▪ FoxH ▪ AppellF1 ▪ HeavisideTheta ▪ DiracComb ▪ Mod ▪ Quotient ▪ Divisible ▪ GCD ▪ Factorial ▪ Binomial ▪ Fibonacci ▪ BernoulliB ▪ StirlingS1 ▪ IntegerDigits ▪ DigitCount ▪ BitAnd ▪ FactorInteger ▪ Prime ▪ PrimePi ▪ EulerPhi ▪ MoebiusMu ▪ DivisorSigma ▪ JacobiSymbol ▪ MultiplicativeOrder ▪ PartitionsP ▪ SquaresR ▪ DirichletL ▪ FunctionSign ▪ FunctionSingularities ▪ NormalDistribution ▪ ChiSquareDistribution ▪ PoissonDistribution ▪ RandomInteger ▪ RandomReal ▪ RandomChoice ▪ RandomPrime ▪ SquareWave ▪ TriangleWave ▪ UnitBox ▪ MandelbrotSetMemberQ ▪ JuliaSetIterationCount ▪ CantorStaircase ▪ N ▪ FunctionExpand ▪ FullSimplify ▪ MathematicalFunctionData ▪ Dt ▪ ImplicitD ▪ Grad ▪ Div ▪ Curl ▪ Laplacian ▪ CoordinateChartData ▪ Series ▪ MinLimit ▪ MaxLimit ▪ DSolve ▪ Minimize ▪ Maximize ▪ Sum ▪ Product ▪ DifferenceQuotient ▪ DifferenceDelta ▪ DiscreteLimit ▪ RSolve ▪ NIntegrate ▪ NDSolve ▪ NMinimize ▪ NSum ▪ AsymptoticIntegrate ▪ AsymptoticDSolveValue ▪ AsymptoticSum ▪ AsymptoticRSolveValue ▪ LaplaceTransform ▪ FourierTransform ▪ Convolve ▪ DiracDelta ▪ Normalize ▪ Orthogonalize ▪ FunctionRange ▪ FunctionDomain ▪ FunctionInjective ▪ FunctionPeriod ▪ ArcLength ▪ Area ▪ Volume ▪ RegionDistance ▪ Derivative ▪ DifferentialRoot ▪ DSolveChangeVariables ▪ IntegrateChangeVariables ▪