WolframRegelkreiseEin Kernbestandteil der
Wolfram Language
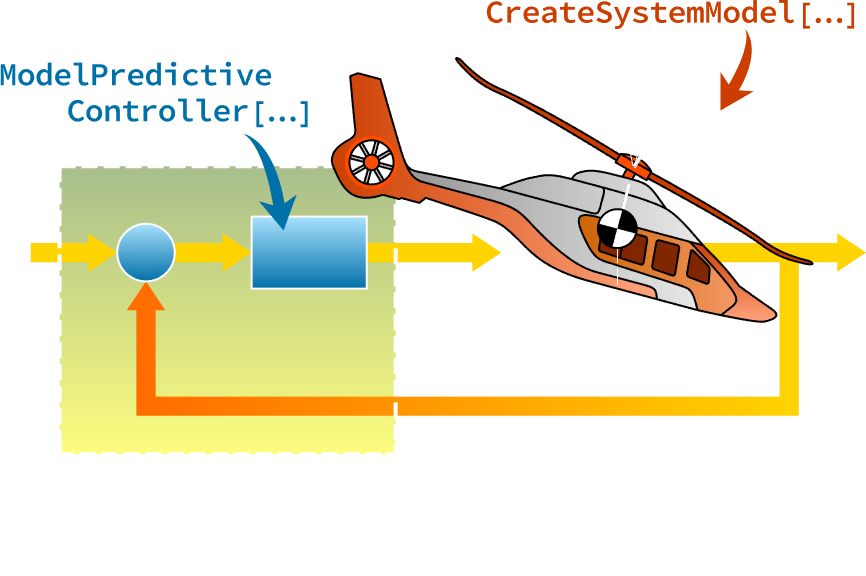
Modellieren, entwerfen, bereitstellen.
Modellieren Sie Ihre Umgebung. Entwerfen Sie einen Regler. Stellen Sie Ihre Entwürfe zur Anwendung bereit. Alles in einem eng integrierten Workflow, der sowohl Lernenden als auch Profis entgegen kommt.
Blockbasierte Modelle
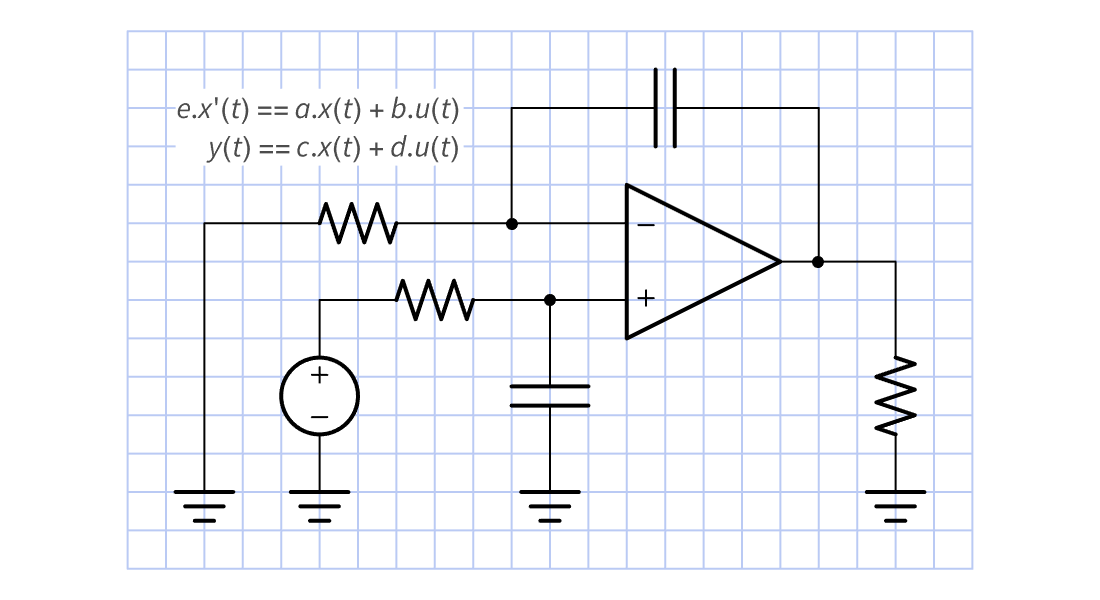
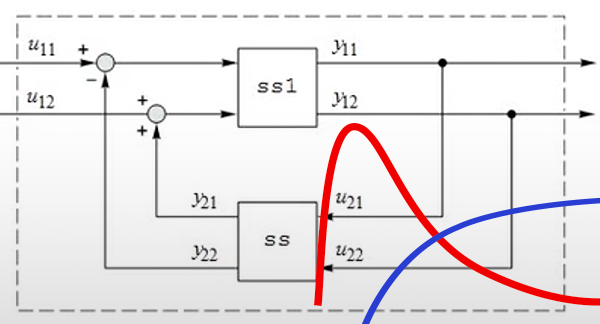
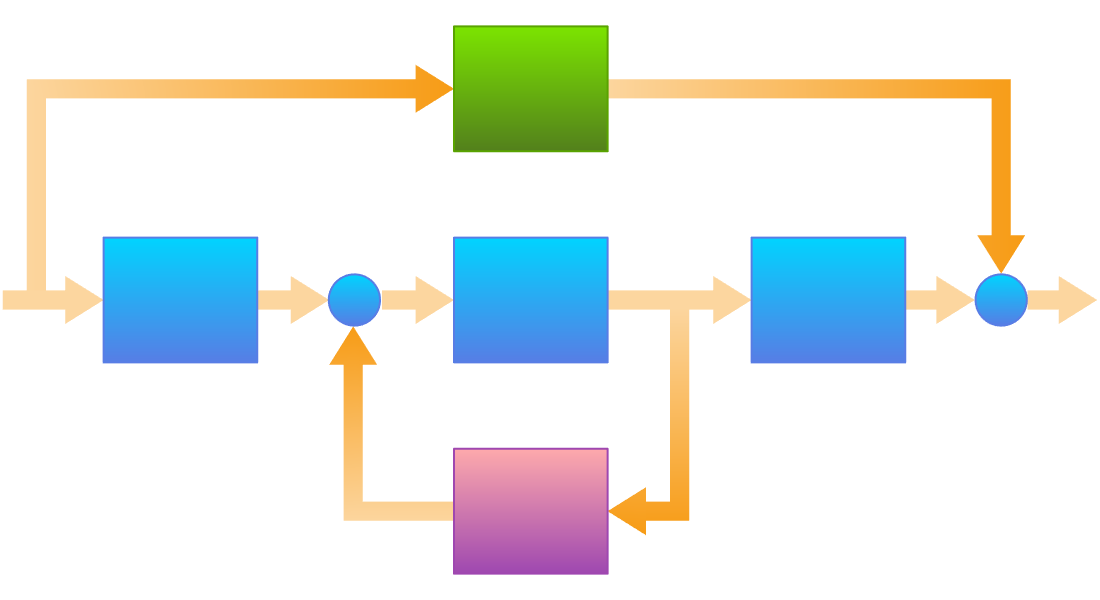
Erstellen Sie Modellblöcke für Zustandsräume oder Übertragungsfunktione direkt oder aus Differential- oder Differenzgleichungen. Verbinden Sie diese zu größeren Systemen. Verwenden Sie die resultierenden Modelle für Analyse, Entwürfe und Anwendungen.
Komponentenbasierte Modelle
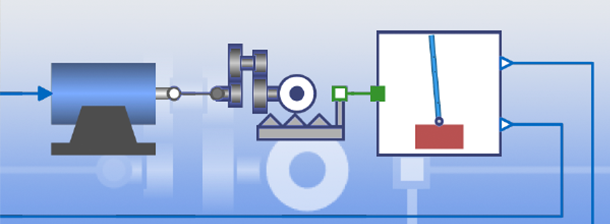
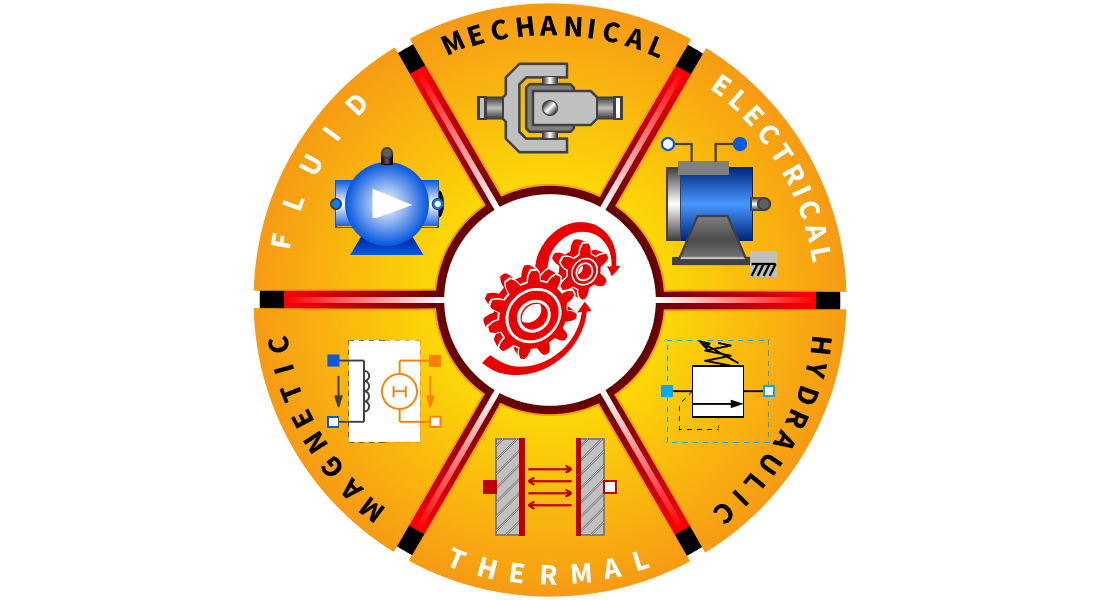
Durch Ziehen, Ablegen (Drag & Drop) und Verbinden von Modellkomponenten wie Legosteine erhalten Sie realitätsgetreue Mehrdomänenmodelle. Verwenden Sie diese für die Simulation, Validierung und zur Ableitung blockbasierter Modelle für den Steuerungsentwurf.
Graphikdesign
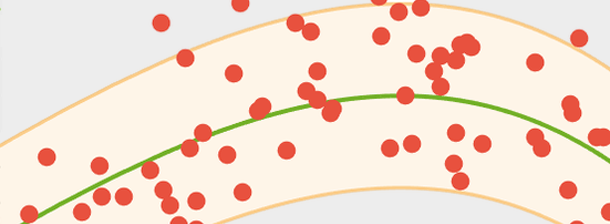
Entwerfen und analysieren Sie Steuerungssysteme mit Hilfe grafischer Techniken wie Bode-, Nyquist-, Wurzelort- und anderen Diagrammen. Typische Beispiele sind Lead-Lag-Entwurf, Stabilitätsanalyse und Robustheitsanalyse.

PID-Entwurf
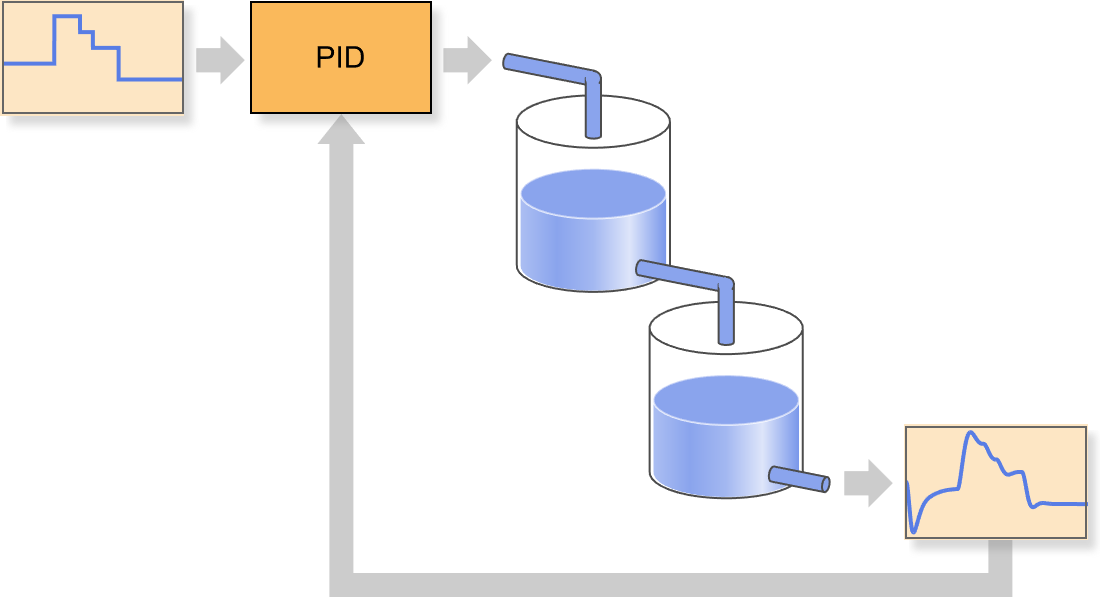
Machen Sie eine automatische Feineinstellung Ihres PID-Reglers auf der Grundlage von Einstellmodellen und -regeln. Verbessern Sie die Systemverfolgung und Störungsunterdrückung. Mit eingebauten Einstellregeln, einschließlich Ziegler-Nichols-Regeln, Cohen-Coon-Regeln und anderen.
LQ-Entwurf
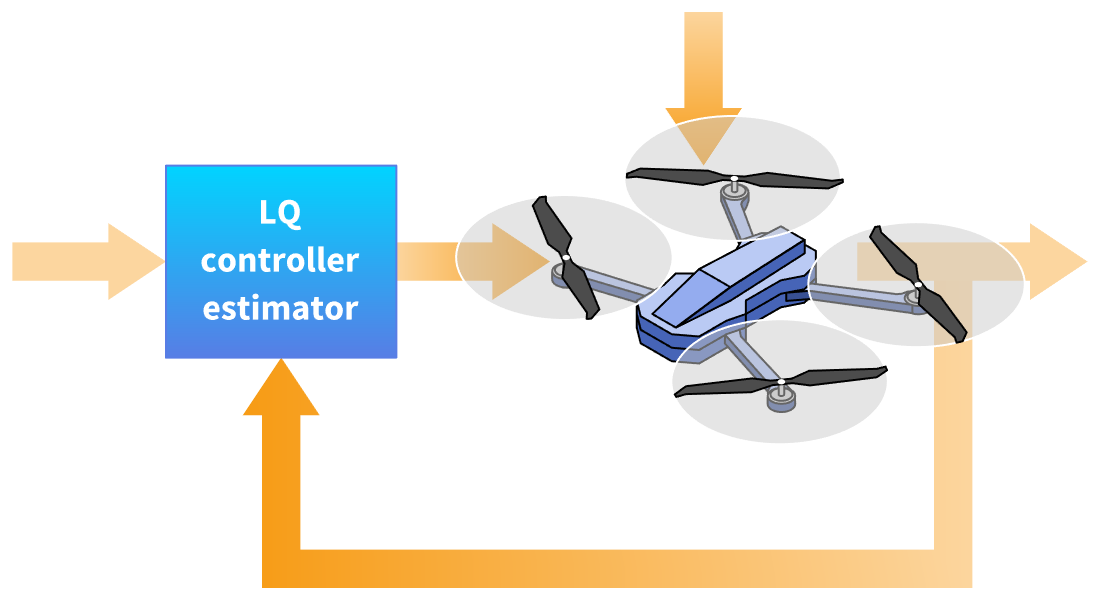
Entwerfen Sie Regler und Schätzer unter Verwendung linearer quadratischer (LQ) Optimierungsmethoden. Lösen Sie Regelungs- oder Nachführprobleme. Integrierte Unterstützung für Standardtechniken, einschließlich LQR, LQG und Kalman.
MPC-Entwurf
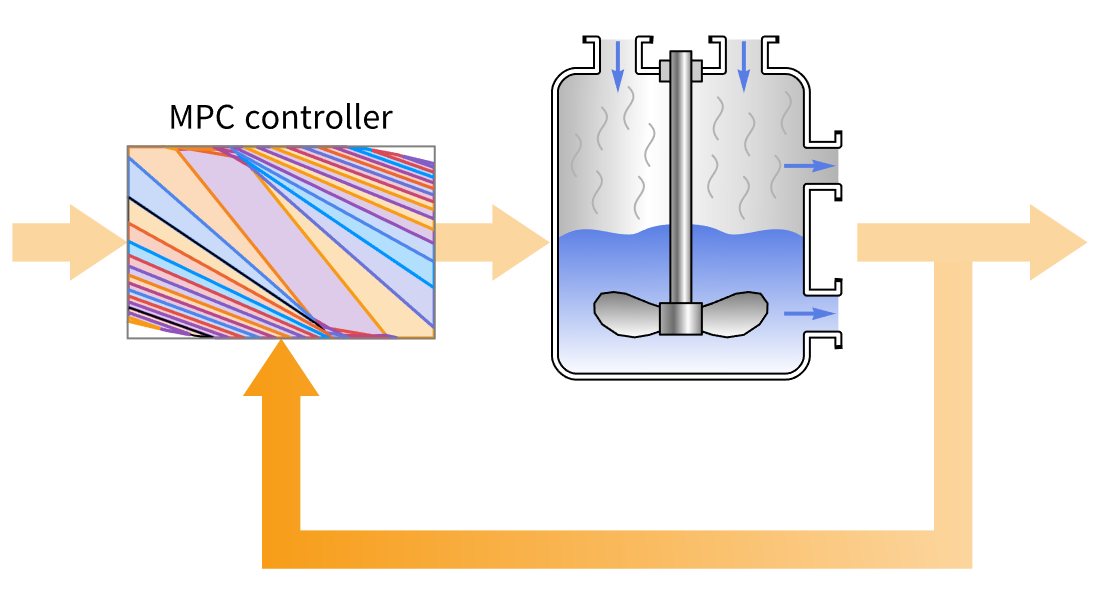
Entwerfen Sie explizite modellprädiktive Regler (MPC) für Anwendungen mit schneller Abtastung und begrenzter Rechenleistung durch automatische Offline-Parameteroptimierung. Lösen Sie eingeschränkte Regelungs- oder Nachführprobleme für 1-, quadrierte 2- oder ∞-normierte Kostenminimierung.
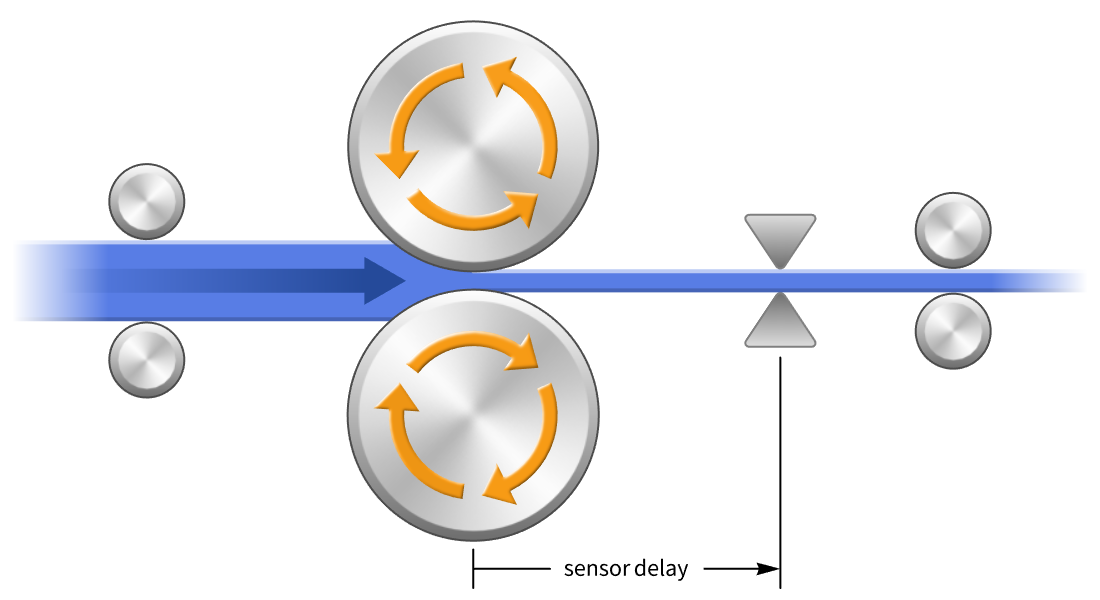
Entwurf mit Verzögerungen und Deskriptorsystemen
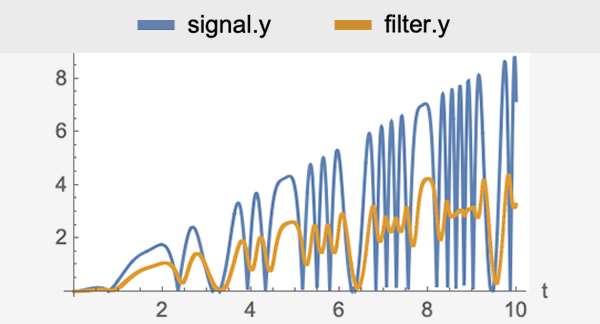
Entwerfen Sie Regler für Modelle mit Verzögerungen und einer Mischung aus dynamischen und algebraischen Gleichungen. Verzögerungen, z. B. durch Kommunikationsverzögerungen, können zu Instabilitäten führen, wenn sie nicht kompensiert werden. Verwenden Sie spezielle Verfahren wie einen Smith-Kompensator oder reduzieren Sie auf Standardmodelle unter Verwendung von Näherungswerten.
Affine und nichtlineare Regler
Entwerfen Sie nichtlineare Regler für Systeme, in denen Nichtlinearitäten eine wichtige Rolle spielen. Dies führt zu einer geringeren Leistungsverschlechterung in Regionen, die weit vom Arbeitspunkt entfernt sind. Simulieren Sie den Einsatz symbolischer Techniken wie rückgekoppelte Linearisierung, Ausgangsregelung und mehr.
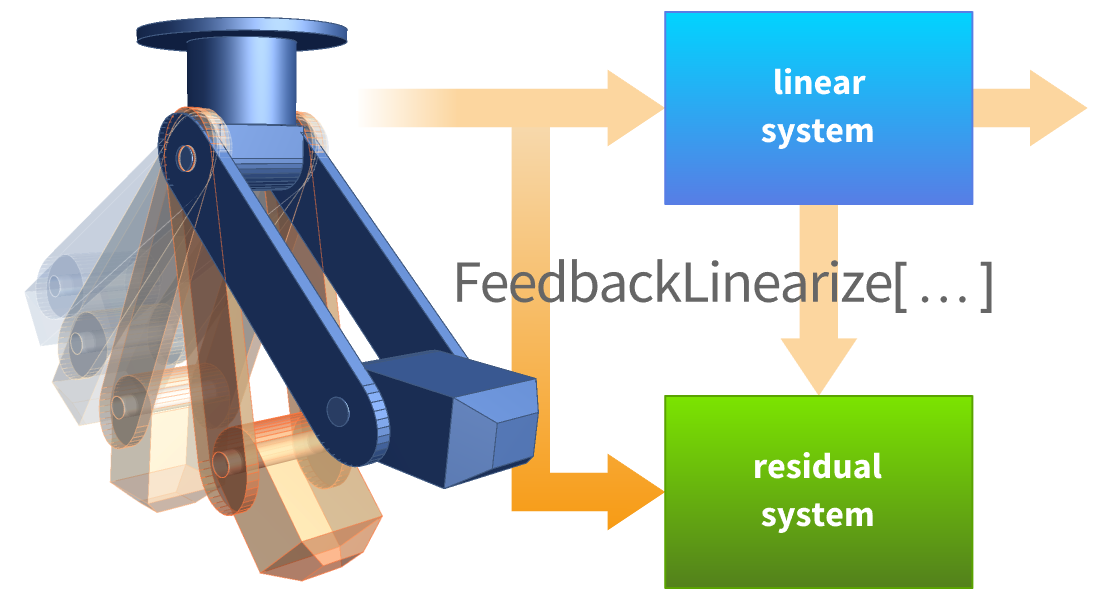
FMI-Bereitstellung
Stellen Sie Steuerungen als Functional Mockup Units (FMUs) für über 100 andere FMI-kompatible Tools bereit. Dies ermöglicht die effektive Zusammenarbeit in einer Umgebung, in der Subsysteme von verschiedenen Unternehmen und Tools entwickelt werden, und die frühzeitige Erkennung von Fehlern und Vermeidung größerer nachgelagerter Integrationsprobleme.

Microcontroller bereitstellen
Nutzen Sie das automatische Generieren und Bereitstellen von Steuerungsentwürfen und Datenerfassungscode für Mikrocontroller. Eliminieren Sie fehleranfällige und langwierige Iterationen des Quellcodes auf unterer Ebene.

Dokumentation für Wolfram Regelkreise
Wolfram Regelkreise ist integrierter Bestandteil der Wolfram Language. Das vollständige System enthält über 6.000 eingebaute Funktionen, die alle Bereiche des Rechnens abdecken—alle sorgfältig integriert, damit sie perfekt zusammenarbeiten.
Vollständiger Umfang & Dokumentation
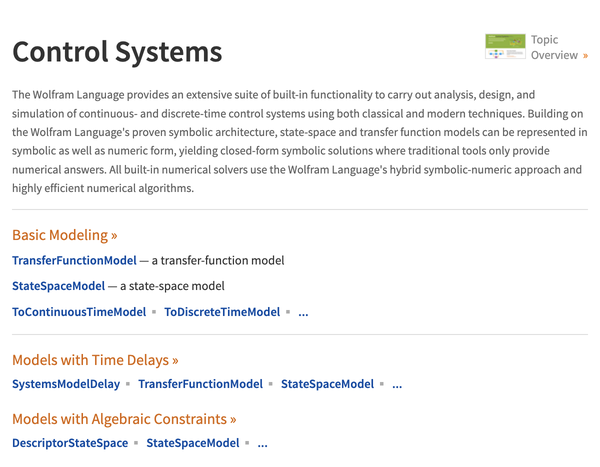 Guide
Guide Guide
Guide Guide
Guide