WolframSistemas de controlUna parte fundamental de
Wolfram Language

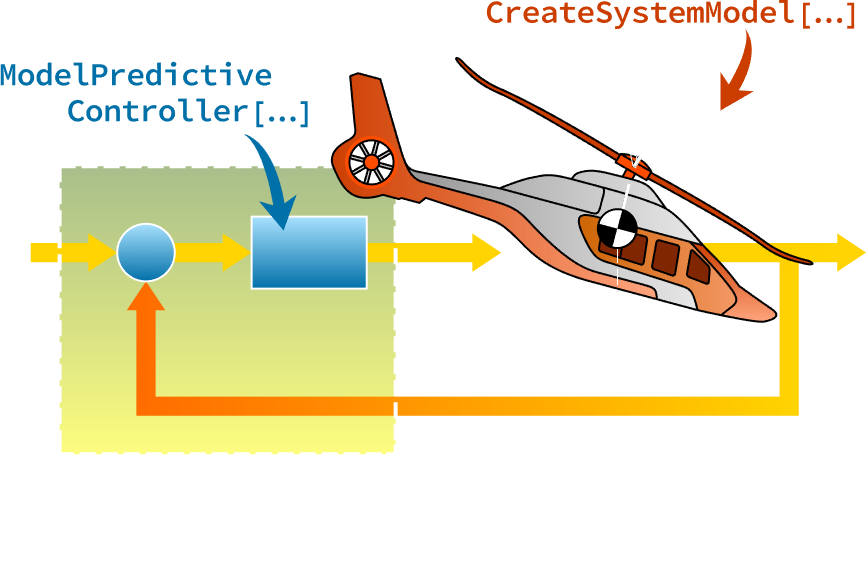
Modele, diseñe, implemente.

Modele el entorno. Diseñe un controlador. Implemente al mundo real. Todo en un flujo de trabajo altamente integrado, desarrollado para estudiantes y profesionales.

Comenzar

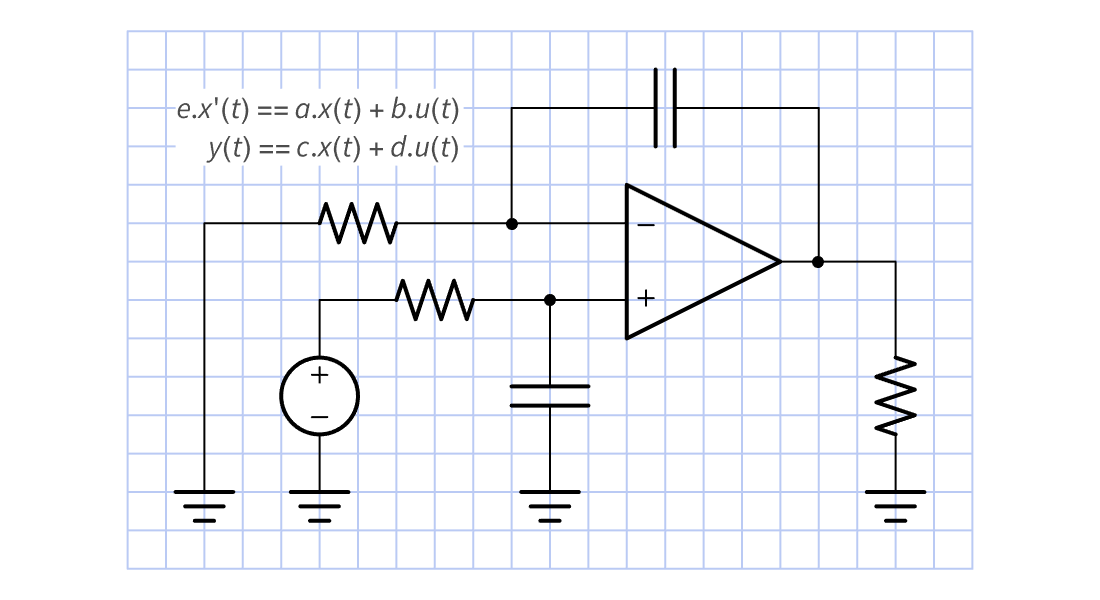
Modelos basados en bloques

Cree bloques de modelos de espacio de estados o funciones de transferencia directamente o a partir de ecuaciones diferenciales o de diferencia. Conéctelos para formar sistemas de mayor tamaño. Use los modelos resultantes para análisis, diseño e implementación.

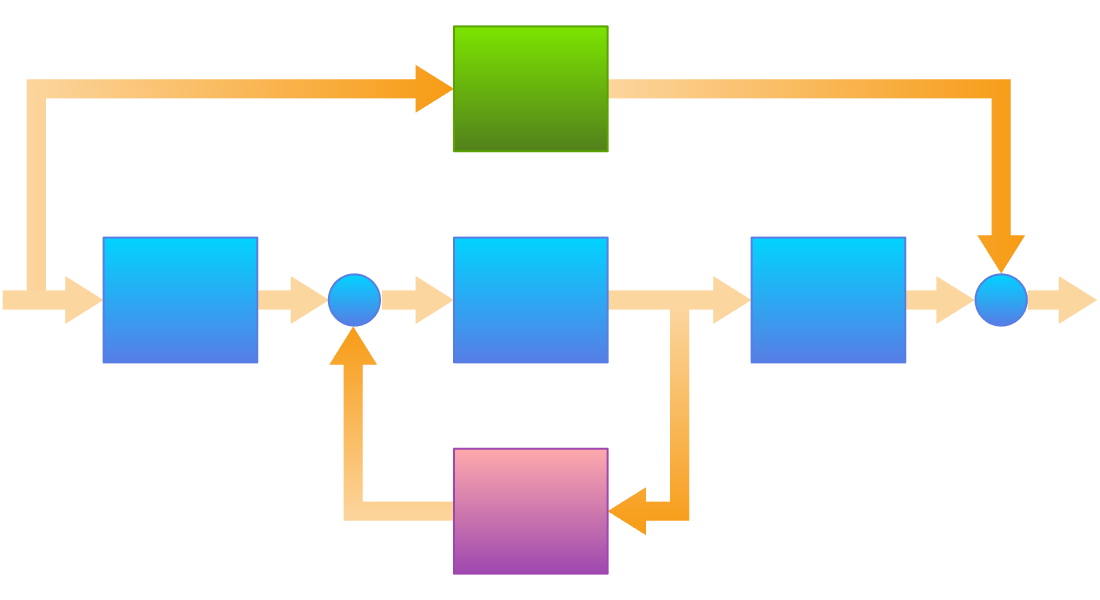
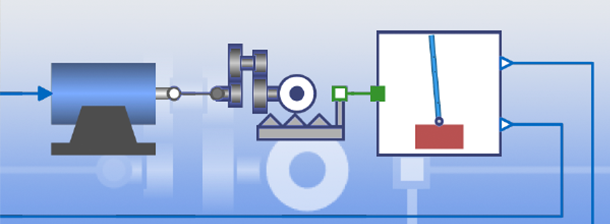
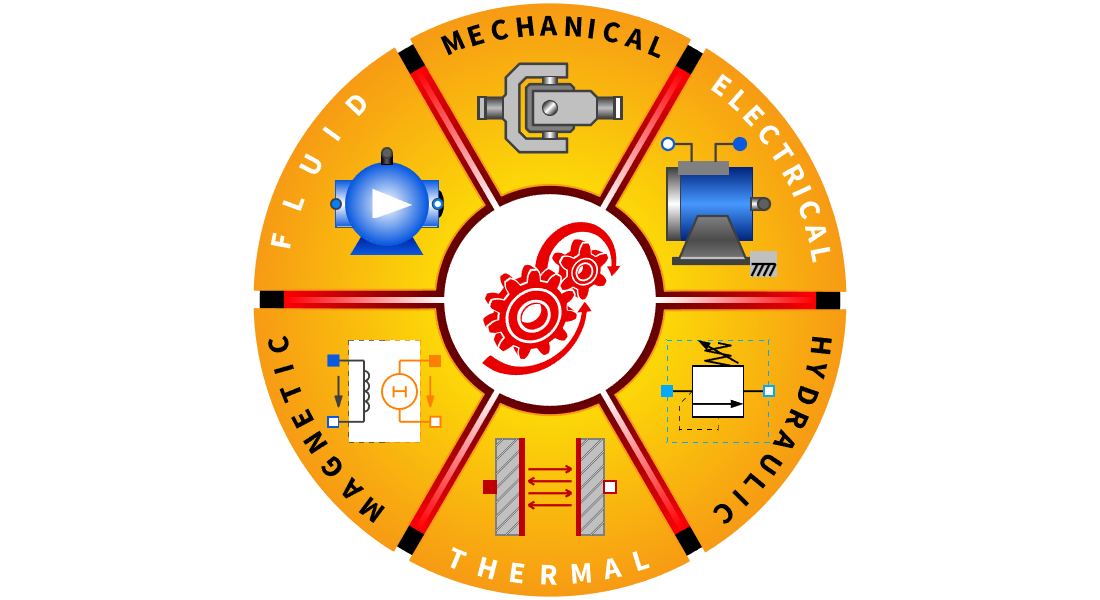
Modelos basados en componentes

Arrastre, suelte y conecte componentes de modelos como piezas de Lego para obtener modelos multidominio de alta fidelidad. Úselos para simulación, validación, y para derivar modelos basados en bloques para el diseño de controles.

Diseño gráfico

Diseñe y analice sistemas de control usando técnicas gráficas tales como Bode, Nyquist, lugar de raíces y otras representaciones gráficas. Los ejemplos típicos incluyen diseño "lead-lag", análisis de estabilidad y análisis de robustez.

Guía para análisis y diseño gráfico

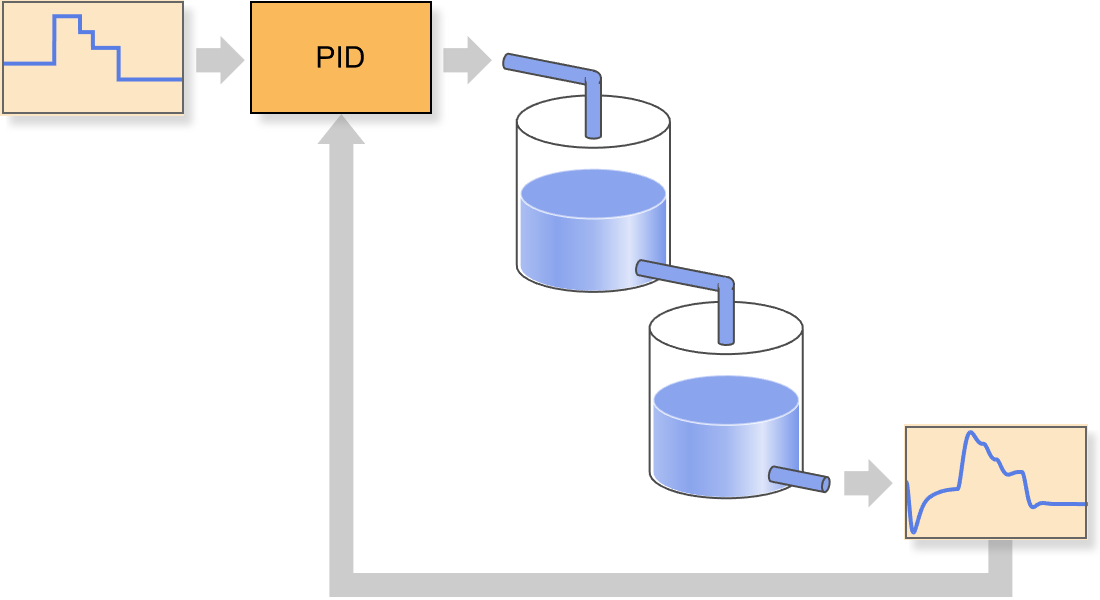
Diseño PID

Ajuste controladores PID automáticamente basándose en modelos y reglas de ajuste. Mejore el seguimiento del sistema y el rechazo de perturbaciones. Incluye reglas de ajuste incorporadas, como las de Ziegler–Nichols, Cohen–Coon y muchas más.

La función PIDTune

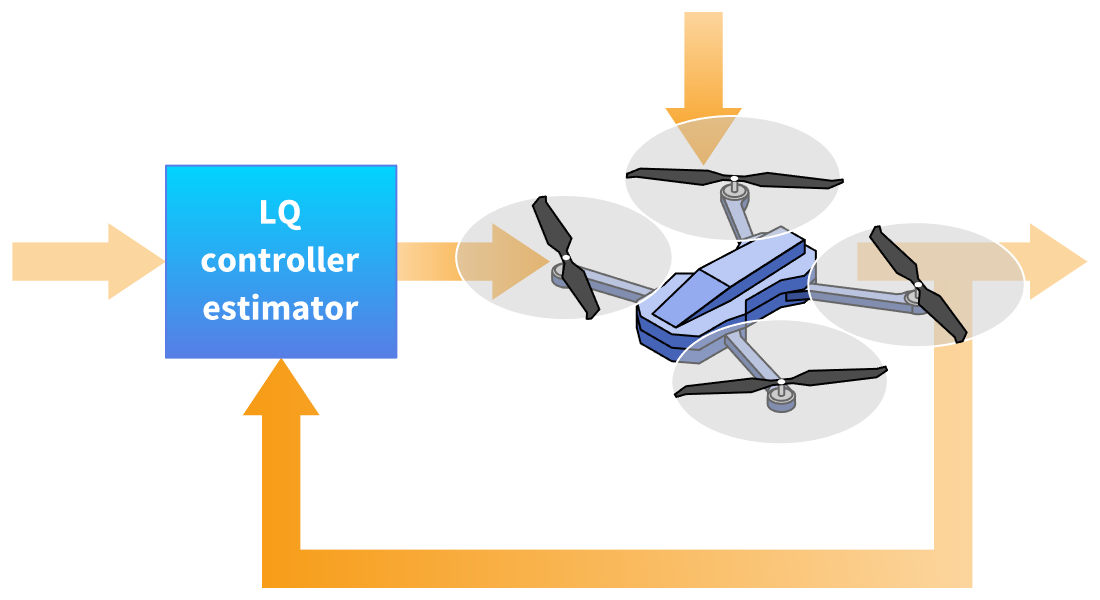
Diseño LQ

Diseñe controladores y estimadores utilizando métodos de optimización cuadrática lineal (LQ por sus siglas en inglés). Resuelva problemas de regulación o seguimiento. Incluye soporte incorporado para técnicas estándar, como LQR, LQG y Kalman.

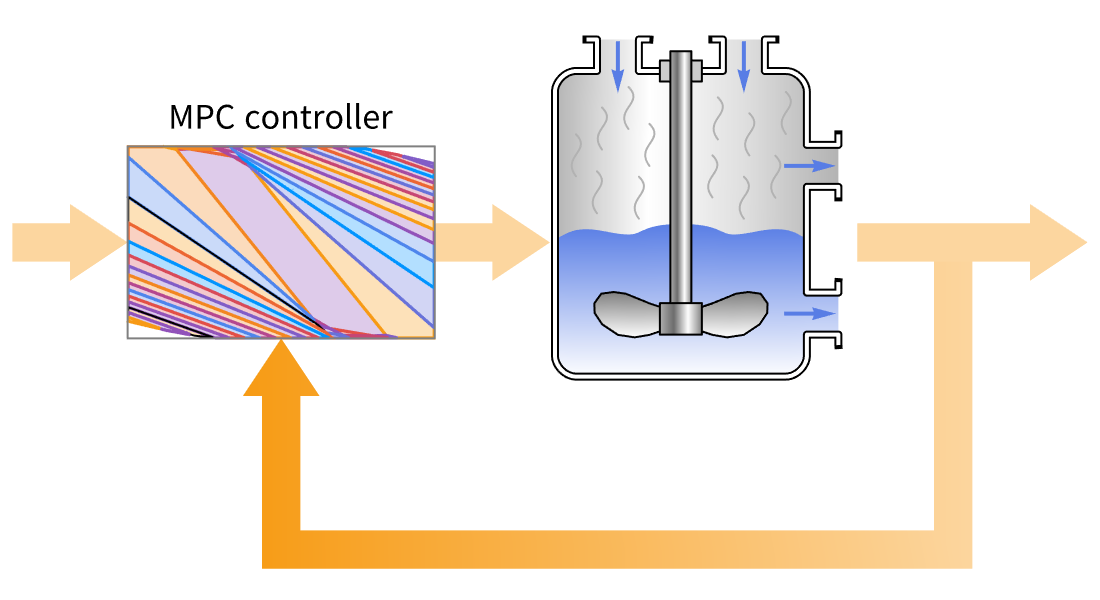
Guía para diseño utilizando modelos de espacio de estados

Diseño de MPC

Diseñe controladores predictivos por modelo (MPC por sus siglas en inglés) explícitos para aplicaciones de muestreo rápido y aquellas con potencia de cálculo limitada, utilizando optimización paramétrica fuera de línea de forma automática. Resuelva problemas de regulación o seguimiento con restricciones para minimización de costos con normas de 1, 2 o ∞ cuadrados.

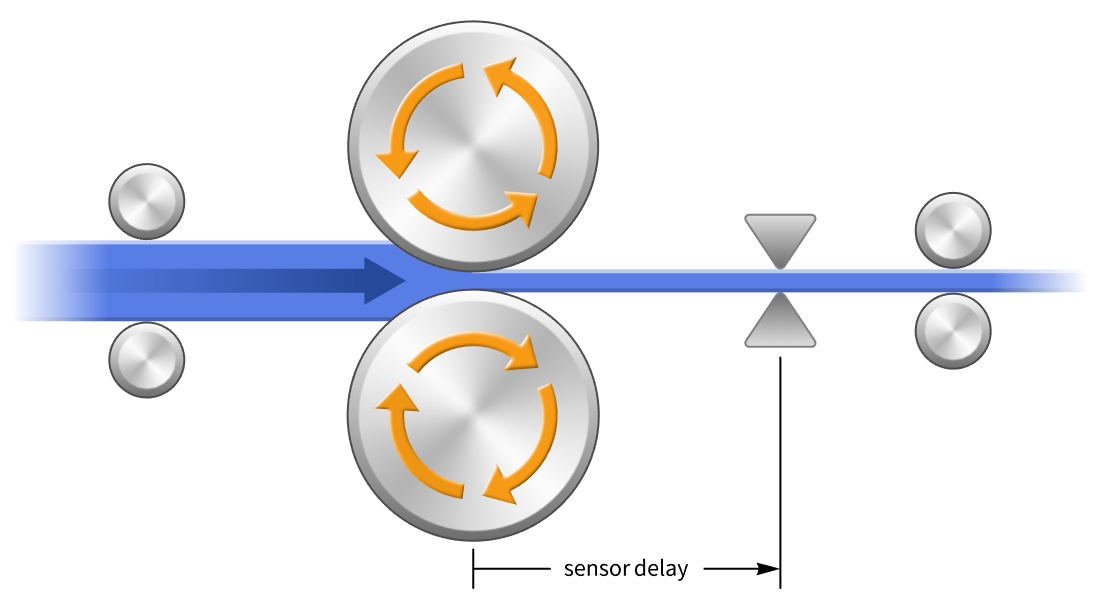
La función ModelPredictiveController

Diseño aplazado y de descriptores

Diseñe controladores para modelos de retardo y una mezcla de ecuaciones dinámicas y algebraicas. Los retardos, originados por demoras en la comunicación, entre otras razones, pueden causar inestabilidad a menos que se compensen. Use procedimientos especializados tales como un compensador de Smith, o reduzca a modelos estándar utilizando aproximaciones.

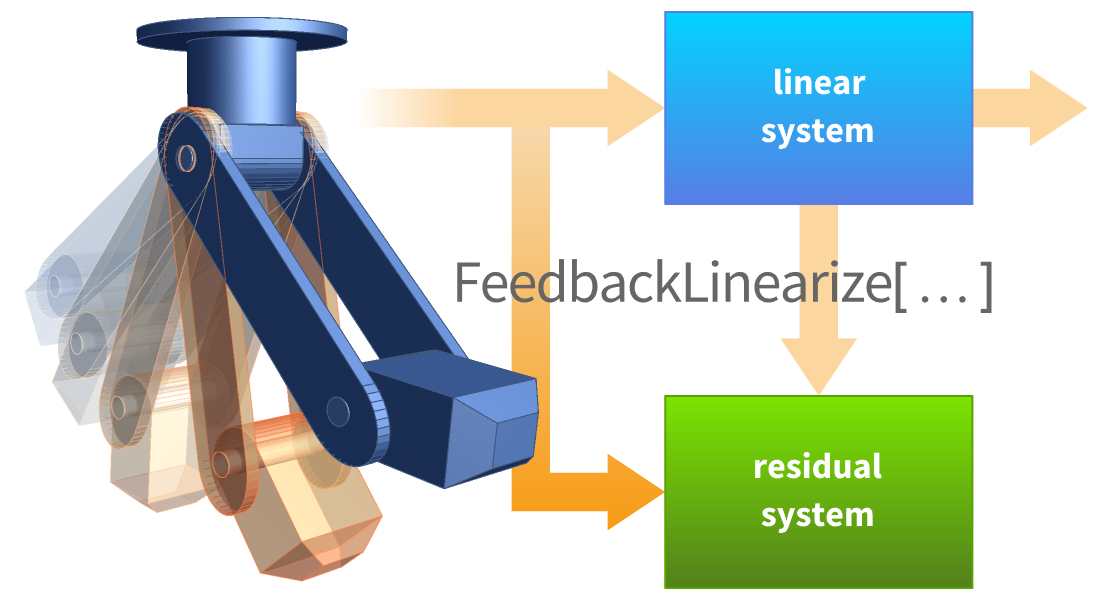
Diseño afín y no lineal

Diseñe controladores no lineales para sistemas en los cuales las no linealidades desempeñan un papel importante. Esto resultará en una degradación de rendimiento menor en regiones alejadas del punto de operación. Use técnicas simbólicas tales como linealización por retroalimentación, regulación de salida y más.

Implementación de FMI

Implemente controladores como unidades de simulación funcional (FMU por sus siglas en inglés) a más de 100 otras herramientas compatibles con FMI. Colabore de manera efectiva en un entorno donde los subsistemas son diseñados por distintas empresas y herramientas. Identifique defectos tempranamente y evite serios problemas de integración más adelante.

Implementación de microcontroladores

Genere e implemente de manera automática diseños de control y código de adquisición de datos a microcontroladores. Elimine iteraciones laboriosas y propensas a errores del código fuente de menor nivel.

Live Playground

This is an interactive notebook—try making your own changes!

Continue exploring more examples:Things to Try

Documentación de Wolfram Sistemas de control

Wolfram Sistemas de control es una parte integrada de Wolfram Language. El sistema completo contiene más de 6000 funciones incorporadas que abarcan todas las áreas de la computación, todas cuidadosamente integradas de manera que trabajen perfectamente en conjunto.

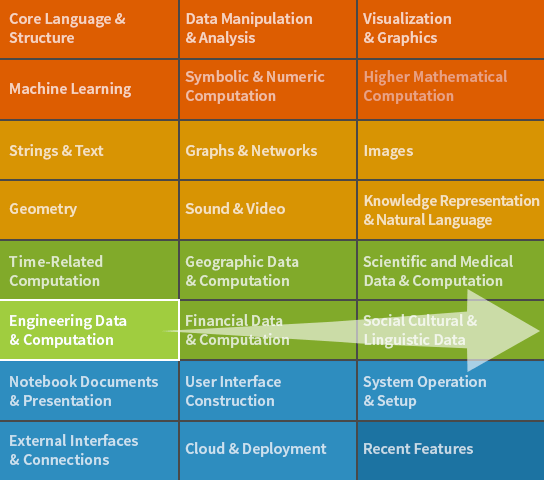
Alcance completo y documentación de
Wolfram Language

Guide

Guía para sistemas de control

Guide

Guía para el kit de microcontroladores

Guide

Guía para análisis y diseño de modelos de sistemas

AffineStateSpaceModel ▪ AsymptoticOutputTracker ▪ BodePlot ▪ CarlemanLinearize ▪ ContinuousTimeModelQ ▪ ControllabilityGramian ▪ ControllabilityMatrix ▪ ControllableDecomposition ▪ ControllableModelQ ▪ DescriptorStateSpace ▪ DiscreteInputOutputModel ▪ DiscreteLQEstimatorGains ▪ DiscreteLQRegulatorGains ▪ DiscreteTimeModelQ ▪ DualSystemsModel ▪ EstimatorGains ▪ EstimatorRegulator ▪ FeedbackLinearize ▪ FeedbackSector ▪ FeedbackSectorStyle ▪ FeedbackType ▪ FullInformationOutputRegulator ▪ GainMargins ▪ GainPhaseMargins ▪ InternallyBalancedDecomposition ▪ JordanModelDecomposition ▪ KalmanEstimator ▪ KroneckerModelDecomposition ▪ LinearizingTransformationData ▪ LQEstimatorGains ▪ LQGRegulator ▪ LQOutputRegulatorGains ▪ LQRegulatorGains ▪ MinimalStateSpaceModel ▪ ModelPredictiveController ▪ NicholsGridLines ▪ NicholsPlot ▪ NonlinearStateSpaceModel ▪ NyquistGridLines ▪ NyquistPlot ▪ ObservabilityGramian ▪ ObservabilityMatrix ▪ ObservableDecomposition ▪ ObservableModelQ ▪ OutputControllabilityMatrix ▪ OutputControllableModelQ ▪ OutputResponse ▪ PhaseMargins ▪ PhaseRange ▪ PIDData ▪ PIDDerivativeFilter ▪ PIDFeedforward ▪ PIDTune ▪ PoleZeroMarkers ▪ RootLocusPlot ▪ SamplingPeriod ▪ SingularValuePlot ▪ SmithDelayCompensator ▪ StabilityMargins ▪ StabilityMarginsStyle ▪ StateFeedbackGains ▪ StateOutputEstimator ▪ StateResponse ▪ StateSpaceModel ▪ StateSpaceRealization ▪ StateSpaceTransform ▪ StateTransformationLinearize ▪ SystemsConnectionsModel ▪ SystemsModelControllerData ▪ SystemsModelDelay ▪ SystemsModelDelayApproximate ▪ SystemsModelDelete ▪ SystemsModelDimensions ▪ SystemsModelExtract ▪ SystemsModelFeedbackConnect ▪ SystemsModelLabels ▪ SystemsModelLinearity ▪ SystemsModelMerge ▪ SystemsModelOrder ▪ SystemsModelParallelConnect ▪ SystemsModelSeriesConnect ▪ SystemsModelStateFeedbackConnect ▪ SystemsModelVectorRelativeOrders ▪ ToContinuousTimeModel ▪ ToDiscreteTimeModel ▪ TransferFunctionCancel ▪ TransferFunctionExpand ▪ TransferFunctionFactor ▪ TransferFunctionModel ▪ TransferFunctionPoles ▪ TransferFunctionZeros ▪ Eigenvalues ▪ Unevaluated ▪ ZTransform ▪ MatrixExp ▪ LaplaceTransform ▪ MatrixLog ▪ MaxIterations ▪ ZeroTest ▪ PadeApproximant ▪ StandardForm ▪ DiscreteShift ▪ IdentityMatrix ▪ D ▪ Inverse ▪ MAProcess ▪ ARProcess ▪ ARMAProcess ▪ ARIMAProcess ▪ SARIMAProcess ▪ SARMAProcess ▪ CreateSystemModel ▪ SquareWave ▪ Cos ▪ Function ▪ Tolerance ▪ Interval ▪ ListPlot ▪ NRoots ▪ PlotMarkers ▪ UnitStep ▪ NDSolve ▪ RecurrenceTable ▪ DSolve ▪ RSolve ▪ InverseLaplaceTransform ▪ InverseZTransform ▪ GreenFunction ▪ Graphics ▪ LineLegend ▪ Dashed ▪ Dotted ▪ Minimize ▪ JordanDecomposition ▪ Eigensystem ▪ SingularValueDecomposition ▪ Solve ▪ NSolve ▪ Listable ▪ LinearSolve ▪ Sin ▪ MatrixRank ▪ Min ▪ Sort ▪ Max ▪ TemporalData ▪ MissingDataMethod ▪ ResamplingMethod ▪ InterpolationOrder ▪ FoldList ▪ Association ▪ Dataset ▪ RecurrenceFilter ▪ TimeSeries ▪ ListConvolve ▪ Det ▪ MonomialList ▪ Block ▪ AlignmentPoint ▪ Center ▪ AspectRatio ▪ GoldenRatio ▪ Axes ▪ AxesLabel ▪ AxesOrigin ▪ AxesStyle ▪ Background ▪ BaselinePosition ▪ BaseStyle ▪ ClippingStyle ▪ ColorFunctionScaling ▪ ColorFunction ▪ ContentSelectable ▪ CoordinatesToolOptions ▪ Epilog ▪ EvaluationMonitor ▪ Exclusions ▪ ExclusionsStyle ▪ Filling ▪ FillingStyle ▪ FormatType ▪ TraditionalForm ▪ Frame ▪ FrameLabel ▪ FrameStyle ▪ FrameTicks ▪ FrameTicksStyle ▪ GridLines ▪ GridLinesStyle ▪ ImageMargins ▪ ImagePadding ▪ ImageSize ▪ LabelingSize ▪ LabelStyle ▪ MaxRecursion ▪ Mesh ▪ MeshFunctions ▪ MeshShading ▪ MeshStyle ▪ Method ▪ PerformanceGoal ▪ $PerformanceGoal ▪ PlotHighlighting ▪ PlotLabel ▪ PlotLabels ▪ PlotLayout ▪ PlotLegends ▪ PlotPoints ▪ PlotRange ▪ Full ▪ PlotRangeClipping ▪ PlotRangePadding ▪ PlotRegion ▪ PlotStyle ▪ PlotTheme ▪ $PlotTheme ▪ PreserveImageOptions ▪ Prolog ▪ RegionFunction ▪ RotateLabel ▪ True ▪ None ▪ ScalingFunctions ▪ False ▪ TargetUnits ▪ Ticks ▪ TicksStyle ▪ WorkingPrecision ▪ MachinePrecision ▪ AbsArgPlot ▪ Total ▪ All ▪ ExternalTypeSignature ▪ Automatic ▪ Normal ▪ Transpose ▪ ItoProcess ▪ SystemModelExamples ▪ SystemModels ▪ SystemModelSimulate ▪ SystemModelMeasurements ▪ SystemModelSimulationData ▪ SystemModelSimulateSensitivity ▪ SystemModelPlot ▪ ParametricPlot ▪ SystemModel ▪ Plot ▪ ListLinePlot ▪ LogPlot ▪ SystemModelParametricSimulate ▪ ParametricFunction ▪ NMinimize ▪ FindMinimum ▪ NMaximize ▪ SystemModelLinearize ▪ FindSystemModelEquilibrium ▪ ConnectSystemModelController ▪ SystemModelReliability ▪ ReliabilityDistribution ▪ SurvivalFunction ▪ StructuralImportance ▪ ButterworthFilterModel ▪ Chebyshev1FilterModel ▪ BiquadraticFilterModel ▪ InputOutputResponse ▪ InputOutputResponseData ▪ RiccatiSolve ▪ DiscreteRiccatiSolve ▪ LyapunovSolve ▪ DiscreteLyapunovSolve ▪