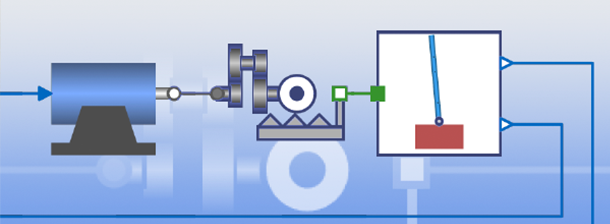
Wolfram制御系WOLFRAM言語の
コアとなる部分
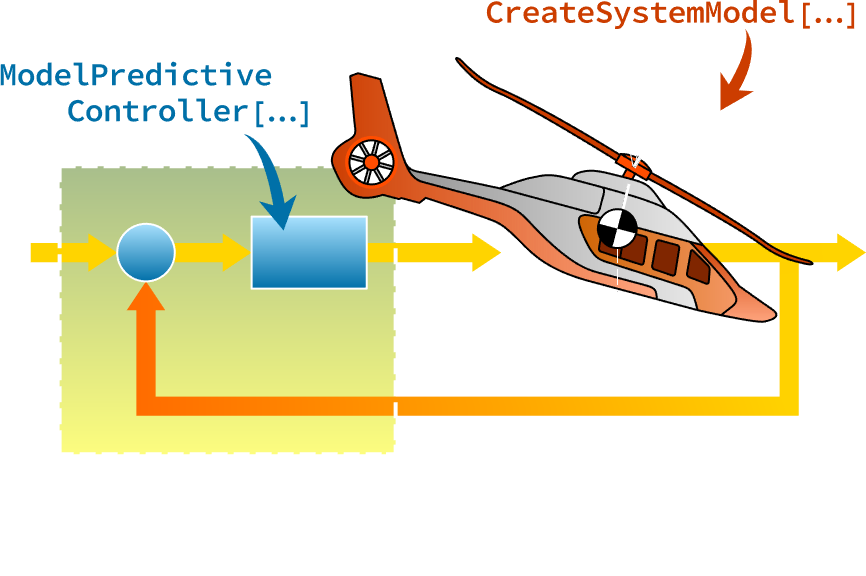
モデリング，設計，配備
環境をモデル化し，コントローラを設計して現実世界に配備するまでのすべての過程を，学生やプロフェッショナルのための高度に統合されたワークフローで行うことができます．
ブロックベースのモデル
微分方程式や差分方程式から状態空間モデルおよび伝達関数モデルのブロックを直接作成したり，ブロックを連結して大きい系から形成したりできます．できたモデルを使って解析，設計，配備が可能です．
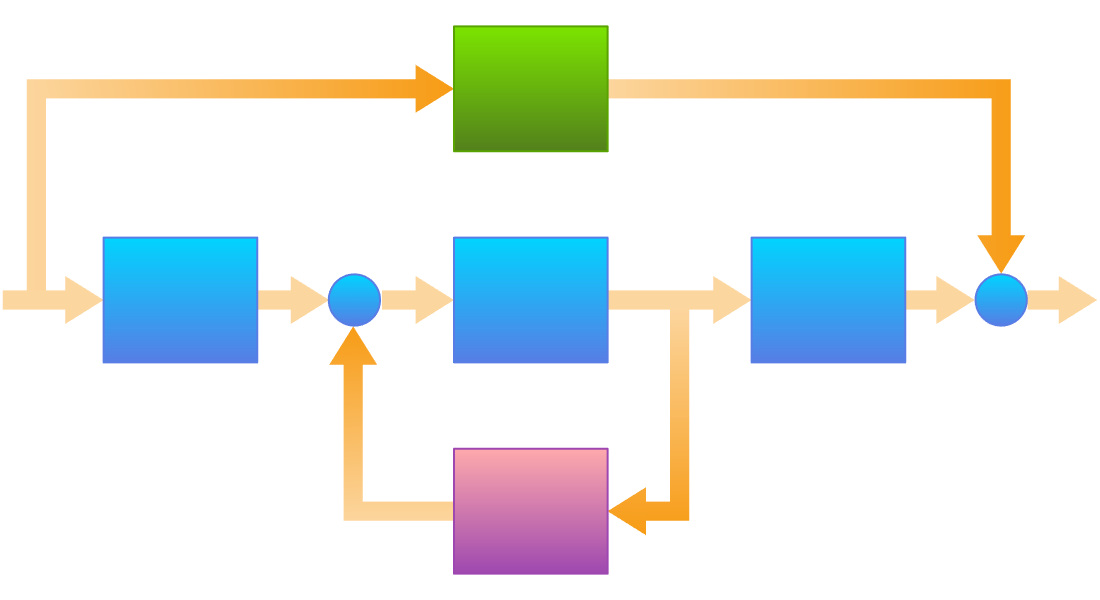
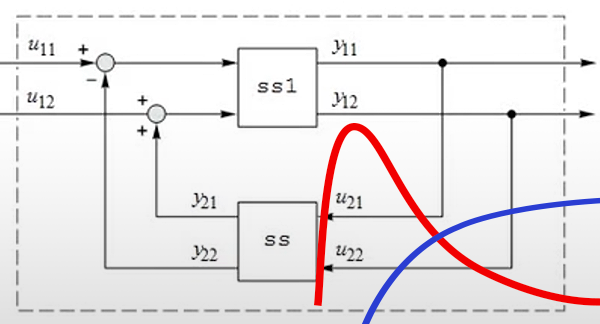
コンポーネントベースのモデル
レゴのピースのようにモデルコンポーネントをドラッグ，ドロップ，接続することで，高忠実度のマルチドメインモデルが得られます．これを使ってシミュレーションや実用検証を行ったり，制御設計のためのブロックベースのモデルを導出したりすることができます．
グラフィカルな設計
ボード線図，ナイキスト線図，根軌跡等のグラフィカルな手法を使って制御系を設計・解析することができます．よく使われる例として，リードラグ設計，安定性解析，ロバスト性解析等があります．
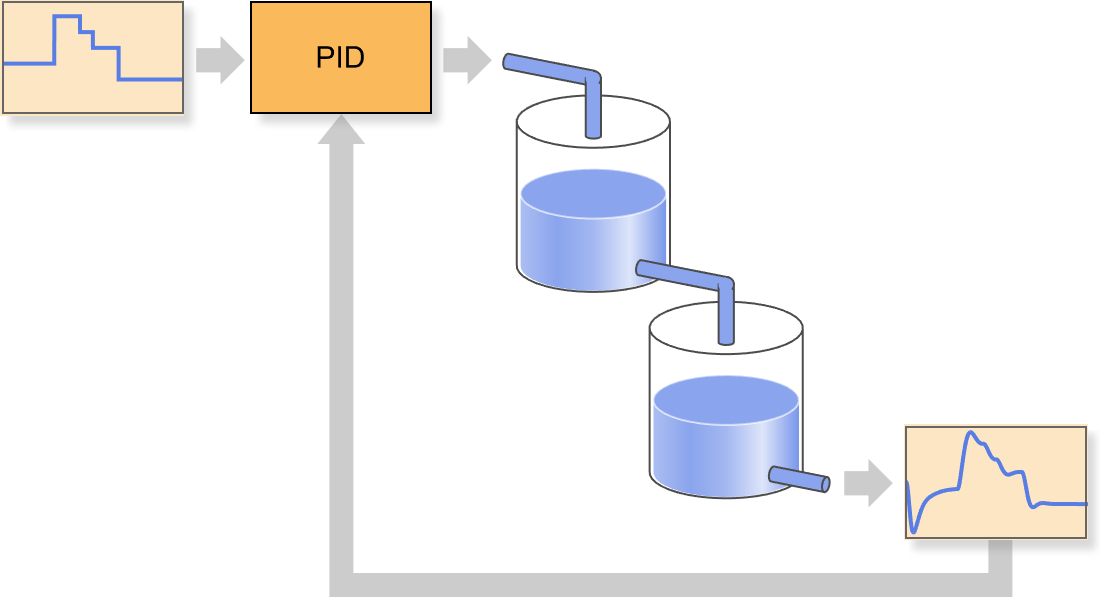
PIDの設計
チューニングのモデルと規則に基づいて自動的にPID制御を調整し，システム追跡および外乱除去機能を向上させます．ジーグラ・ニコルス，コーヘン・クーン等のチューニング法が組み込まれています．
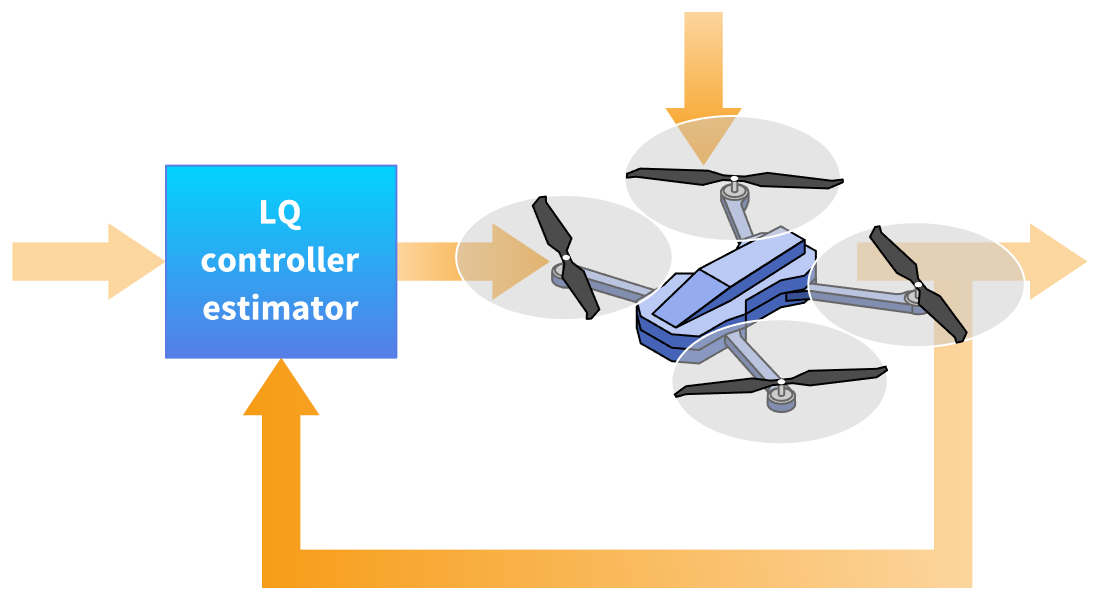
LQの設計
線形二次(LQ)最適化を使って制御器と推定器を設計し，調整問題や追跡問題を解決することができます．LQR，LQG，カルマンを含む標準的な手法のサポートが組み込まれています．
MPCの設計
高速サンプリングアプリケーションや，自動的にオフラインのパラメトリック最適化を使うことによって計算力が限定されているアプリケーションのための，明示的なモデル予測制御器(MPC)が設計できます．１ノルム，平方2ノルム，∞ノルムのコスト最小化についての制約条件付きの調整問題や追跡問題を解きます．
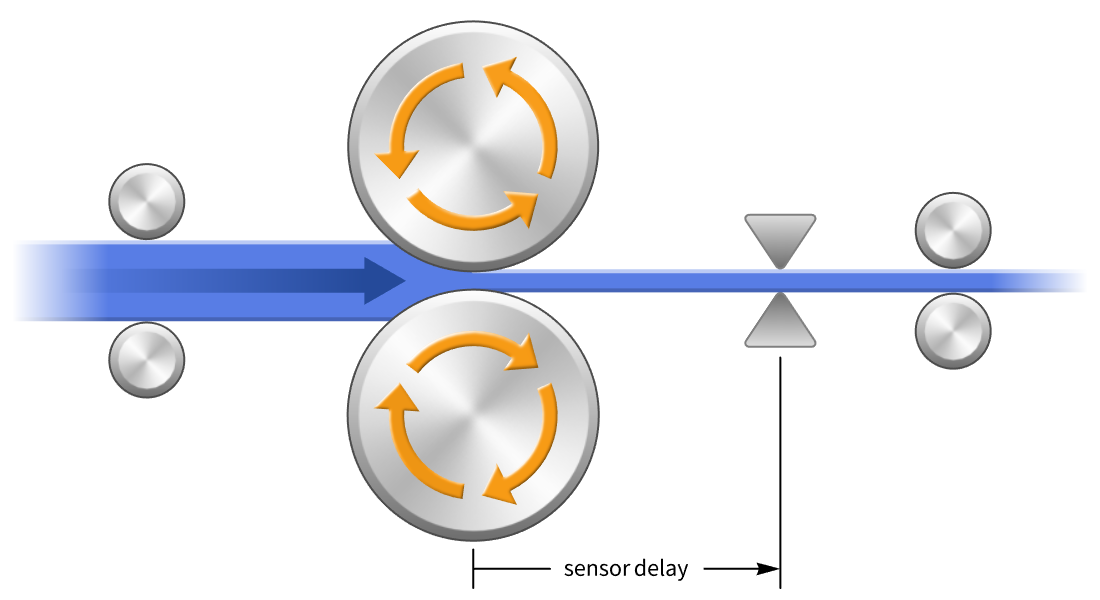
遅延設計と記述子設計
遅延方程式および動的・代数方程式の混合方程式を持つモデルの制御器を設計することができます．通信の時間差等による遅延は，補正されなければ不安定性を引き起こします．スミス補償器等の特別な手順を使ったり，近似を使って標準モデルに変換したりします．
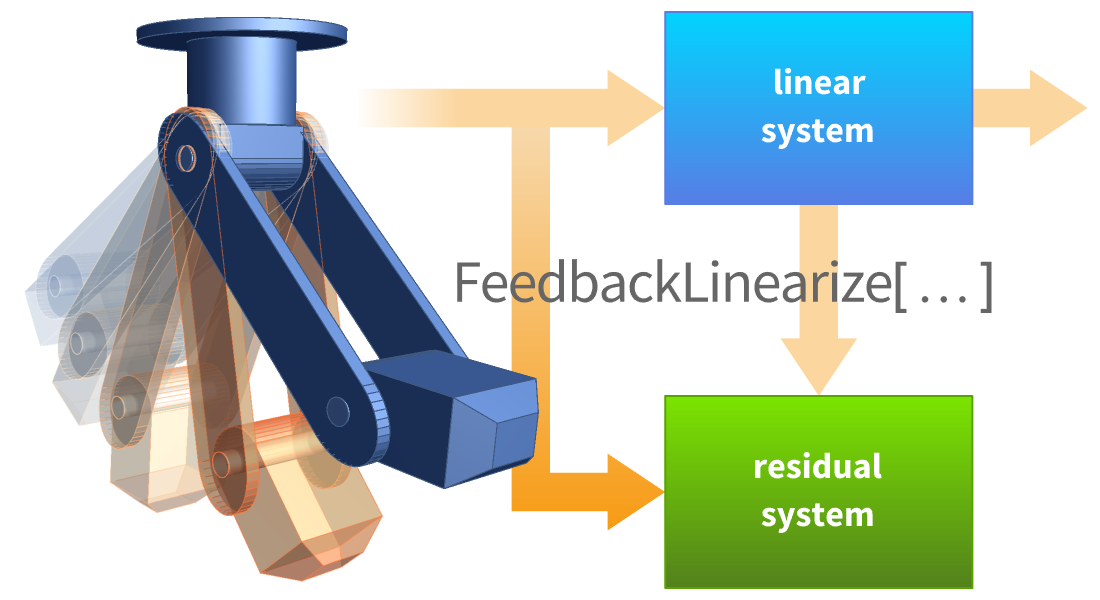
アフィン設計と非線形設計
非線形性が重要な役割を果たす系についての非線形制御器が設計できます．これは結果的に操作点から遠い領域における性能の劣化を減少させます．フィードバックの線形化や出力レギュレーション等の記号的手法を使います．
FMIの配備
100を超える他のFMI対応ツールにFunctional Mockup Unit (FMU)を配備することができます．サブシステムが異なるさまざまな会社やツールで設計される環境において効率的に共同作業を進めることができます．欠陥を早期に発見して，下流の統合問題が大きくなるのを妨げます．
マイクロコントローラの配備
制御設計およびデータ取得コードを自動的に生成し，マイクロコントローラに配備します．退屈な低レベルソースコードの反復を取り除き，起こりやすいエラーが排除できます．
制御系に関するWolframドキュメント
Wolfram 制御系は，Wolfram言語に統合されています．全システムに計算の全分野を網羅する6,000個を超える組込み関数が含まれており，そのすべてが綿密に統合されているため，完全に一体となって作動します．
全領域とドキュメント
制御系の分野でWolfram製品を使い始める
Wolfram|OneまたはMathematicaからWolfram言語にアクセスする
