WolframSistemas de ControlePARTE CENTRAL DA
WOLFRAM LANGUAGE

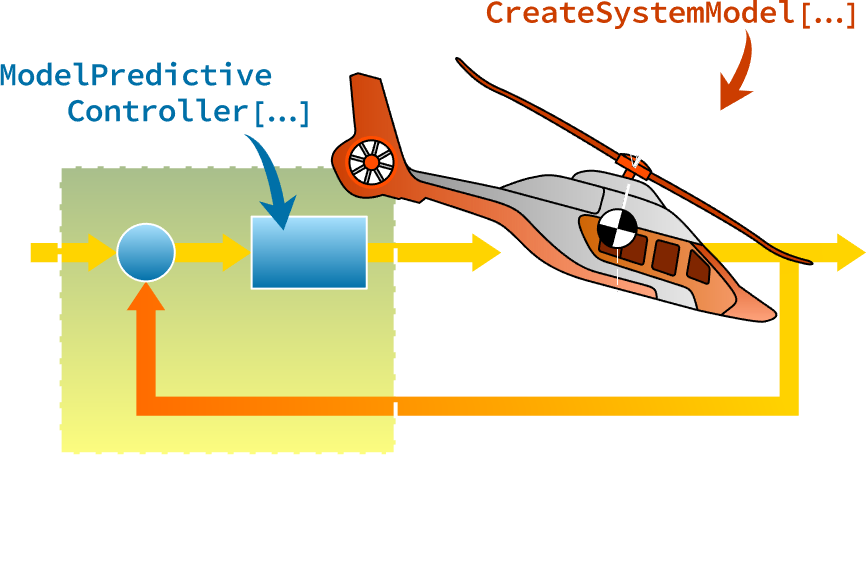
Modele, Desenhe, Implemente.

Modele o ambiente. Desenhe um controlador. Implemente no mundo real. Tudo em um fluxo de trabalho altamente integrado, desenvolvido para aprendizes e profissionais.

Comece agora mesmo

Modelos com Base em Blocos

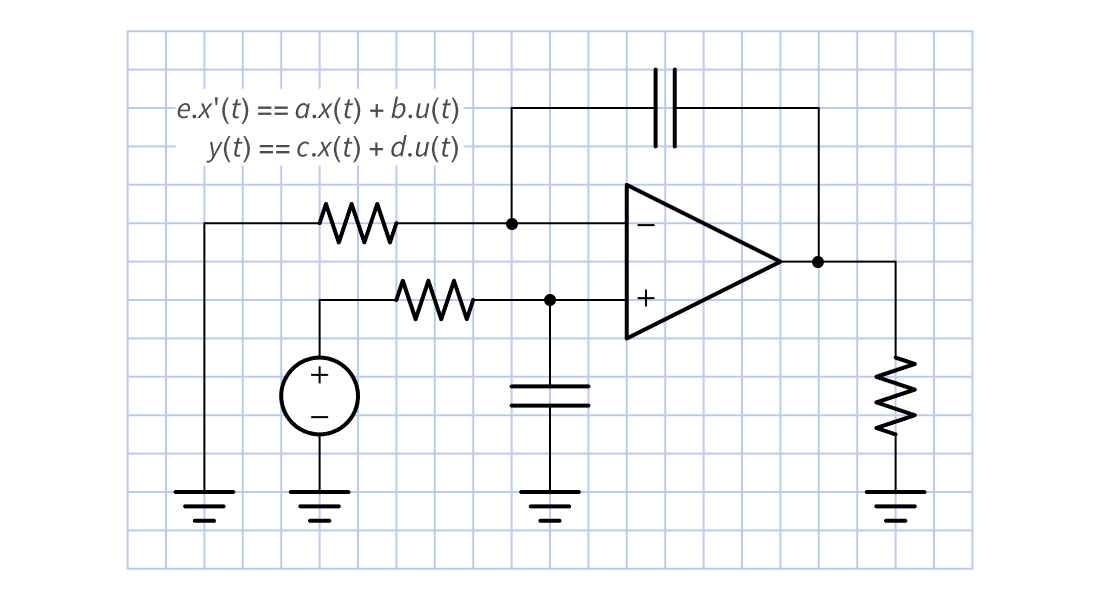
Crie blocos de modelos de espaço de estados ou função de transferência diretamente ou a partir de equações diferenciais ou de diferenças. Conecte-os para formar sistemas maiores. Utilize os modelos resultantes para análise, desenho e implementação.

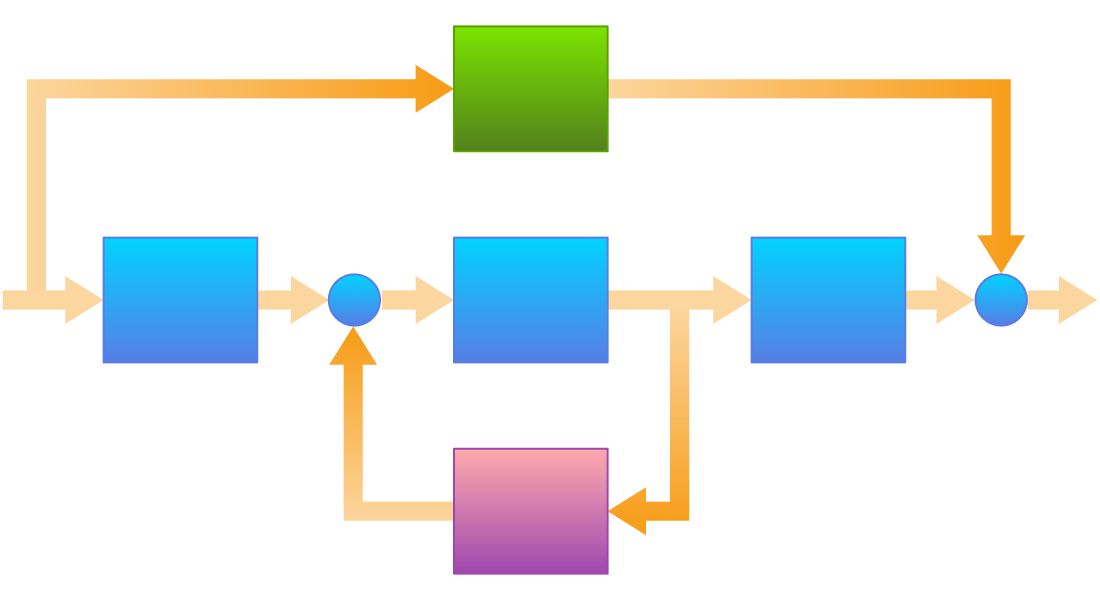
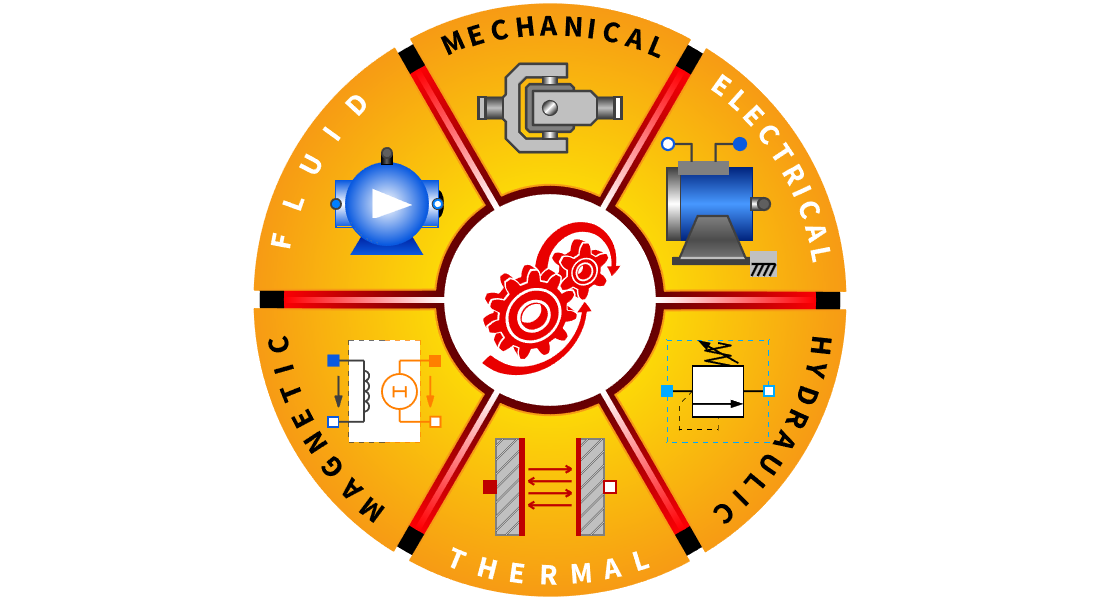
Modelos com Base em Componentes

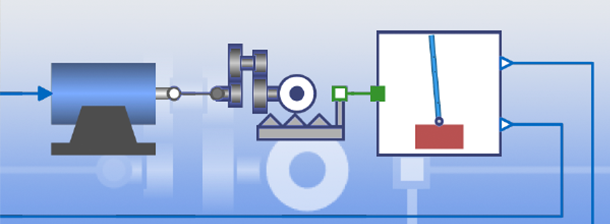
Arraste, solte e conecte os componentes do modelo como peças de Lego para obter modelos multidomínio de alta fidelidade. Utilize-os para simulação, validação e para derivar modelos baseados em blocos para o projeto de controle.

Design Gráfico

Desenhe e analise sistemas de controle utilizando técnicas gráficas como Bode, Nyquist, locus de raízes e outros gráficos. Exemplos comuns incluem o projeto de compensadores lead-lag, análise de estabilidade e análise de robustez.

Guia para Design e Análise Gráfica

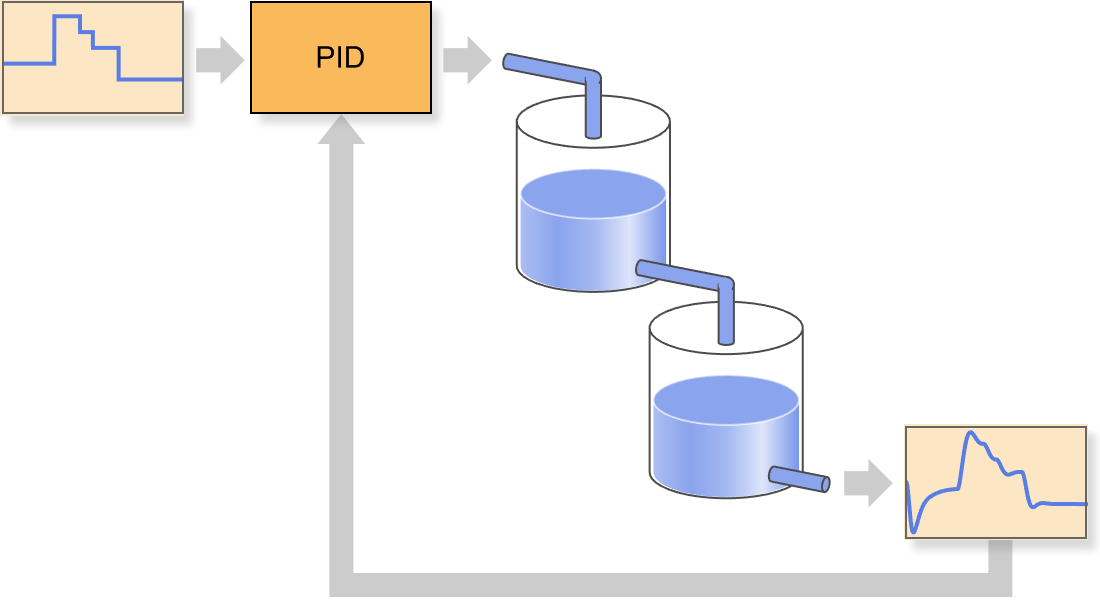
Design de PID

Ajuste automaticamente controladores PID com base em modelos e regras de ajuste. Melhore o rastreamento do sistema e a rejeição de perturbações. Possui regras de ajuste embutidas, incluindo Ziegler-Nichols, Cohen-Coon e várias outras.

Função PIDTune

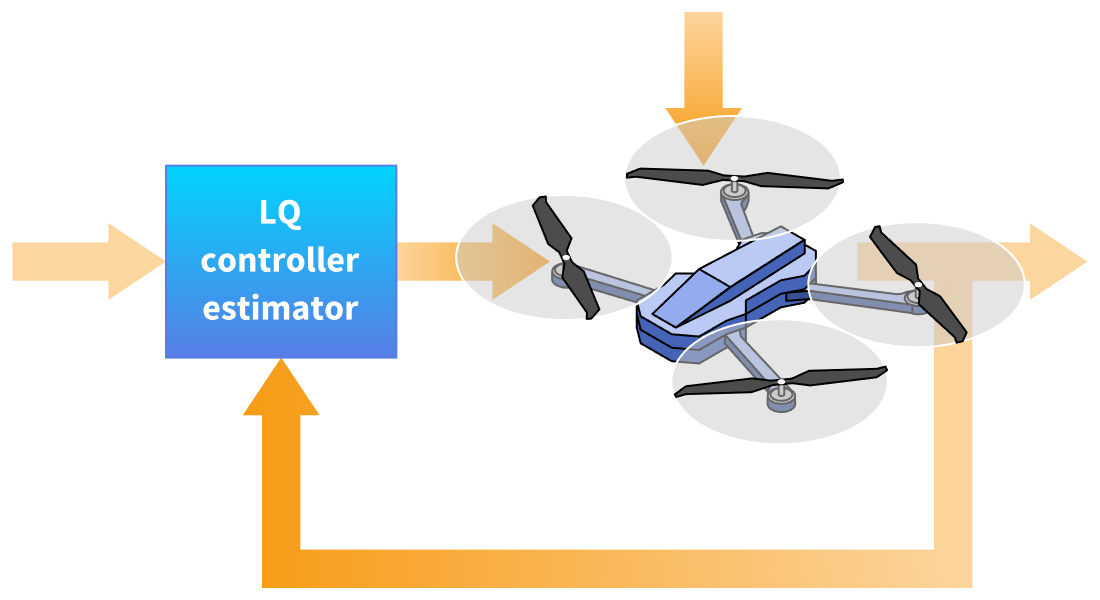
Design de LQ

Desenhe controladores e estimadores utilizando métodos de otimização linear quadrática (LQ). Resolva problemas de regulação ou rastreamento. Possui suporte embutido para técnicas padrão, incluindo LQR, LQG e Kalman.

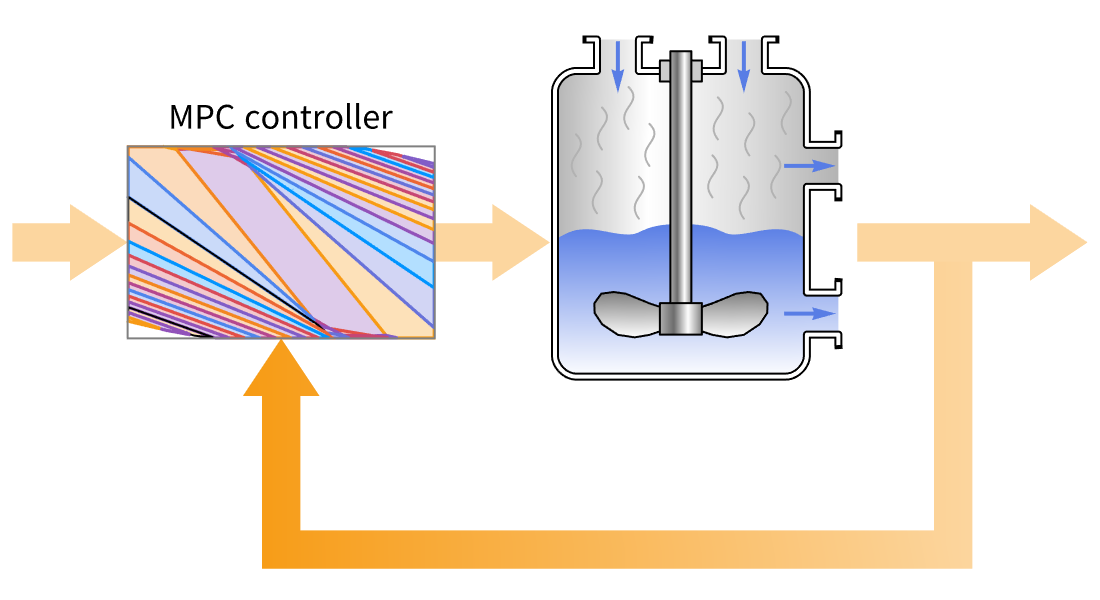
Guia para Design usando Modelos de Espaço de Estado

Design de MPC

Desenhe controladores preditivos de modelo explícito (MPC) para aplicações de amostragem rápida e aquelas com poder computacional limitado, utilizando automaticamente a otimização paramétrica offline. Resolva problemas de regulação ou rastreamento com restrições, minimizando custos com norma 1, norma ao quadrado 2 ou norma infinito.

Função ModelPredictiveController

Design de Controladores com Atrasos e Descritores

Desenhe controladores para modelos com atrasos e uma mistura de equações dinâmicas e algébricas. Atrasos, como atrasos de comunicação, podem causar instabilidades a menos que sejam compensados. Utilize procedimentos especializados, como um compensador de Smith, ou reduza os modelos a modelos padrão usando aproximações.

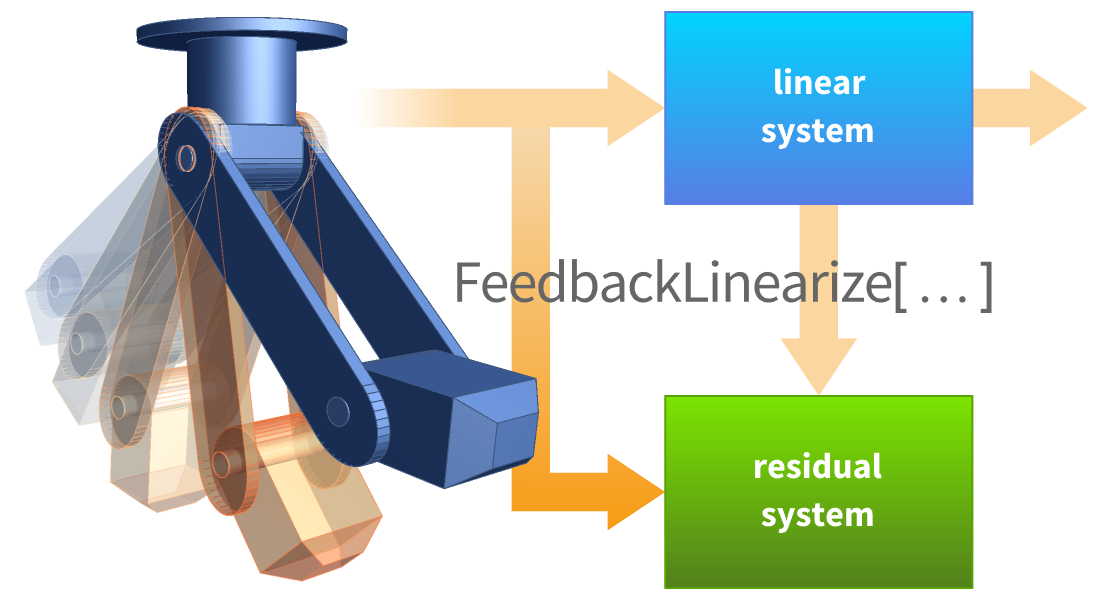
Design de Controle Afim e Não Linear

Desenhe controladores não lineares para sistemas nos quais as não linearidades desempenham um papel importante. Isso resulta em menor degradação de desempenho em regiões distantes do ponto de operação. Utilize técnicas simbólicas, como linearização por realimentação, regulação de saída e outras.

Implementação de FMI

Implemente controladores como Unidades de Simulação Funcional (Functional Mockup Units - FMUs) em mais de 100 outras ferramentas compatíveis com o FMI (Functional Mockup Interface). Colabore de forma eficaz em um ambiente em que subsistemas são projetados por diferentes empresas e ferramentas. Identifique defeitos precocemente e evite grandes problemas de integração futura.

Implementação de Microcontroladores

Gere e implemente automaticamente projetos de controle e código de aquisição de dados em microcontroladores. Elimine iterações propensas a erros e tediosas de código-fonte de nível inferior.

Live Playground

This is an interactive notebook—try making your own changes!

Continue exploring more examples:Things to Try

Documentação para Wolfram Sistemas de Controle

Wolfram Sistemas de Controle é uma parte embutida da Wolfram Language. Todo o sistema contém mais de 6 mil funções integradas, abrangendo todas as áreas da computação — tudo cuidadosamente integrado para que funcione perfeitamente em conjunto.

Wolfram Language
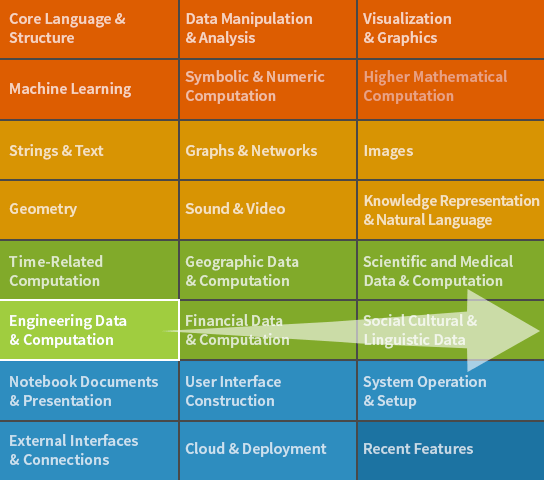
Escopo Completo & Documentação

Guide

Guia para Sistemas de Controle

Guide

Guia do Kit de Microcontroladores

Guide

Guia de Análise de Mpdelos e Design de Sistema

AffineStateSpaceModel ▪ AsymptoticOutputTracker ▪ BodePlot ▪ CarlemanLinearize ▪ ContinuousTimeModelQ ▪ ControllabilityGramian ▪ ControllabilityMatrix ▪ ControllableDecomposition ▪ ControllableModelQ ▪ DescriptorStateSpace ▪ DiscreteInputOutputModel ▪ DiscreteLQEstimatorGains ▪ DiscreteLQRegulatorGains ▪ DiscreteTimeModelQ ▪ DualSystemsModel ▪ EstimatorGains ▪ EstimatorRegulator ▪ FeedbackLinearize ▪ FeedbackSector ▪ FeedbackSectorStyle ▪ FeedbackType ▪ FullInformationOutputRegulator ▪ GainMargins ▪ GainPhaseMargins ▪ InternallyBalancedDecomposition ▪ JordanModelDecomposition ▪ KalmanEstimator ▪ KroneckerModelDecomposition ▪ LinearizingTransformationData ▪ LQEstimatorGains ▪ LQGRegulator ▪ LQOutputRegulatorGains ▪ LQRegulatorGains ▪ MinimalStateSpaceModel ▪ ModelPredictiveController ▪ NicholsGridLines ▪ NicholsPlot ▪ NonlinearStateSpaceModel ▪ NyquistGridLines ▪ NyquistPlot ▪ ObservabilityGramian ▪ ObservabilityMatrix ▪ ObservableDecomposition ▪ ObservableModelQ ▪ OutputControllabilityMatrix ▪ OutputControllableModelQ ▪ OutputResponse ▪ PhaseMargins ▪ PhaseRange ▪ PIDData ▪ PIDDerivativeFilter ▪ PIDFeedforward ▪ PIDTune ▪ PoleZeroMarkers ▪ RootLocusPlot ▪ SamplingPeriod ▪ SingularValuePlot ▪ SmithDelayCompensator ▪ StabilityMargins ▪ StabilityMarginsStyle ▪ StateFeedbackGains ▪ StateOutputEstimator ▪ StateResponse ▪ StateSpaceModel ▪ StateSpaceRealization ▪ StateSpaceTransform ▪ StateTransformationLinearize ▪ SystemsConnectionsModel ▪ SystemsModelControllerData ▪ SystemsModelDelay ▪ SystemsModelDelayApproximate ▪ SystemsModelDelete ▪ SystemsModelDimensions ▪ SystemsModelExtract ▪ SystemsModelFeedbackConnect ▪ SystemsModelLabels ▪ SystemsModelLinearity ▪ SystemsModelMerge ▪ SystemsModelOrder ▪ SystemsModelParallelConnect ▪ SystemsModelSeriesConnect ▪ SystemsModelStateFeedbackConnect ▪ SystemsModelVectorRelativeOrders ▪ ToContinuousTimeModel ▪ ToDiscreteTimeModel ▪ TransferFunctionCancel ▪ TransferFunctionExpand ▪ TransferFunctionFactor ▪ TransferFunctionModel ▪ TransferFunctionPoles ▪ TransferFunctionZeros ▪ Eigenvalues ▪ Unevaluated ▪ ZTransform ▪ MatrixExp ▪ LaplaceTransform ▪ MatrixLog ▪ MaxIterations ▪ ZeroTest ▪ PadeApproximant ▪ StandardForm ▪ DiscreteShift ▪ IdentityMatrix ▪ D ▪ Inverse ▪ MAProcess ▪ ARProcess ▪ ARMAProcess ▪ ARIMAProcess ▪ SARIMAProcess ▪ SARMAProcess ▪ CreateSystemModel ▪ SquareWave ▪ Cos ▪ Function ▪ Tolerance ▪ Interval ▪ ListPlot ▪ NRoots ▪ PlotMarkers ▪ UnitStep ▪ NDSolve ▪ RecurrenceTable ▪ DSolve ▪ RSolve ▪ InverseLaplaceTransform ▪ InverseZTransform ▪ GreenFunction ▪ Graphics ▪ LineLegend ▪ Dashed ▪ Dotted ▪ Minimize ▪ JordanDecomposition ▪ Eigensystem ▪ SingularValueDecomposition ▪ Solve ▪ NSolve ▪ Listable ▪ LinearSolve ▪ Sin ▪ MatrixRank ▪ Min ▪ Sort ▪ Max ▪ TemporalData ▪ MissingDataMethod ▪ ResamplingMethod ▪ InterpolationOrder ▪ FoldList ▪ Association ▪ Dataset ▪ RecurrenceFilter ▪ TimeSeries ▪ ListConvolve ▪ Det ▪ MonomialList ▪ Block ▪ AlignmentPoint ▪ Center ▪ AspectRatio ▪ GoldenRatio ▪ Axes ▪ AxesLabel ▪ AxesOrigin ▪ AxesStyle ▪ Background ▪ BaselinePosition ▪ BaseStyle ▪ ClippingStyle ▪ ColorFunctionScaling ▪ ColorFunction ▪ ContentSelectable ▪ CoordinatesToolOptions ▪ Epilog ▪ EvaluationMonitor ▪ Exclusions ▪ ExclusionsStyle ▪ Filling ▪ FillingStyle ▪ FormatType ▪ TraditionalForm ▪ Frame ▪ FrameLabel ▪ FrameStyle ▪ FrameTicks ▪ FrameTicksStyle ▪ GridLines ▪ GridLinesStyle ▪ ImageMargins ▪ ImagePadding ▪ ImageSize ▪ LabelingSize ▪ LabelStyle ▪ MaxRecursion ▪ Mesh ▪ MeshFunctions ▪ MeshShading ▪ MeshStyle ▪ Method ▪ PerformanceGoal ▪ $PerformanceGoal ▪ PlotHighlighting ▪ PlotLabel ▪ PlotLabels ▪ PlotLayout ▪ PlotLegends ▪ PlotPoints ▪ PlotRange ▪ Full ▪ PlotRangeClipping ▪ PlotRangePadding ▪ PlotRegion ▪ PlotStyle ▪ PlotTheme ▪ $PlotTheme ▪ PreserveImageOptions ▪ Prolog ▪ RegionFunction ▪ RotateLabel ▪ True ▪ None ▪ ScalingFunctions ▪ False ▪ TargetUnits ▪ Ticks ▪ TicksStyle ▪ WorkingPrecision ▪ MachinePrecision ▪ AbsArgPlot ▪ Total ▪ All ▪ ExternalTypeSignature ▪ Automatic ▪ Normal ▪ Transpose ▪ ItoProcess ▪ SystemModelExamples ▪ SystemModels ▪ SystemModelSimulate ▪ SystemModelMeasurements ▪ SystemModelSimulationData ▪ SystemModelSimulateSensitivity ▪ SystemModelPlot ▪ ParametricPlot ▪ SystemModel ▪ Plot ▪ ListLinePlot ▪ LogPlot ▪ SystemModelParametricSimulate ▪ ParametricFunction ▪ NMinimize ▪ FindMinimum ▪ NMaximize ▪ SystemModelLinearize ▪ FindSystemModelEquilibrium ▪ ConnectSystemModelController ▪ SystemModelReliability ▪ ReliabilityDistribution ▪ SurvivalFunction ▪ StructuralImportance ▪ ButterworthFilterModel ▪ Chebyshev1FilterModel ▪ BiquadraticFilterModel ▪ InputOutputResponse ▪ InputOutputResponseData ▪ RiccatiSolve ▪ DiscreteRiccatiSolve ▪ LyapunovSolve ▪ DiscreteLyapunovSolve ▪