WolframFEMEin Kernbestandteil der
Wolfram Language

Finite-Elemente-Methode.
Ob Anfänger oder Expertin, Wolfram FEM erfasst das Verhalten Ihrer Konstruktion durch die Bereitstellung von multiphysikalischen partiellen Differentialgleichungsmodellen, Solvern und nahtlosen Post-Processing-Funktionen, vollständig integriert mit ausgefeilten Geometrie- und Visualisierungsfunktionen.
Geometrische Modellierung
Entwerfen Sie präzise Simulationen. Erstellen Sie geometrische Modelle aus mehreren Materialien mit booleschen Operationen oder impliziten Beschreibungen oder rekonstruieren Sie sie aus Punktdaten, Bildern, geografischen Karten und mehr. Importieren Sie viele CAD- und andere Geometriedateiformate wie STEP, DXF und STL.
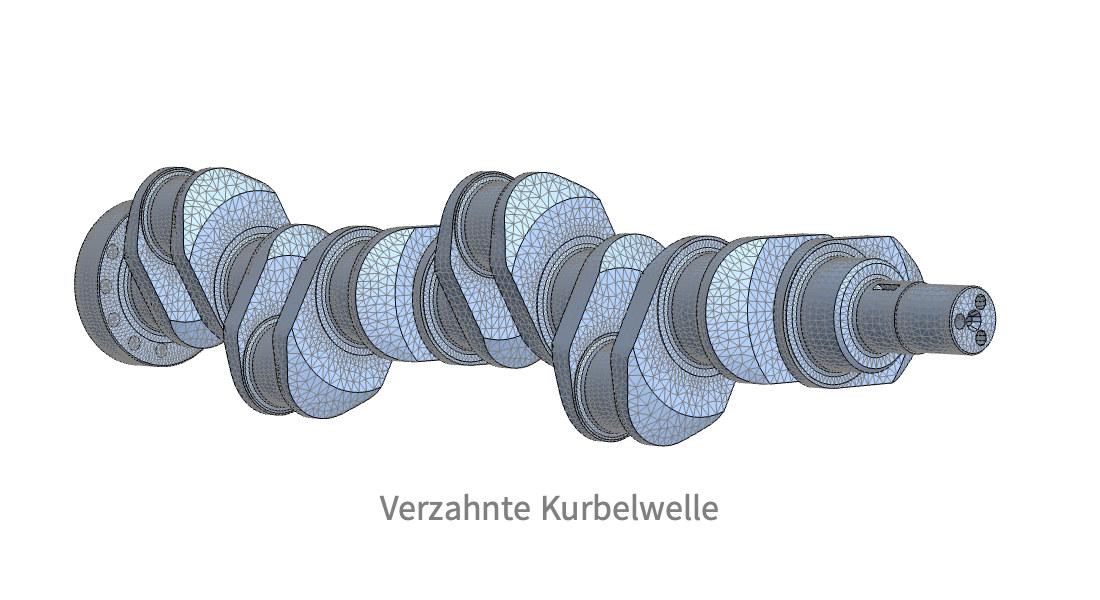
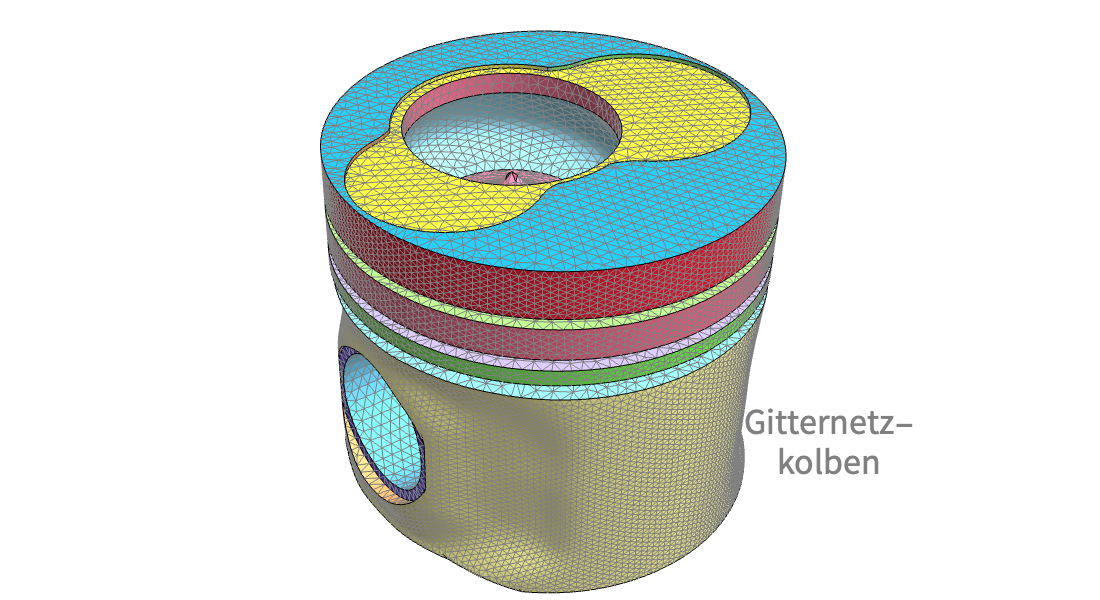
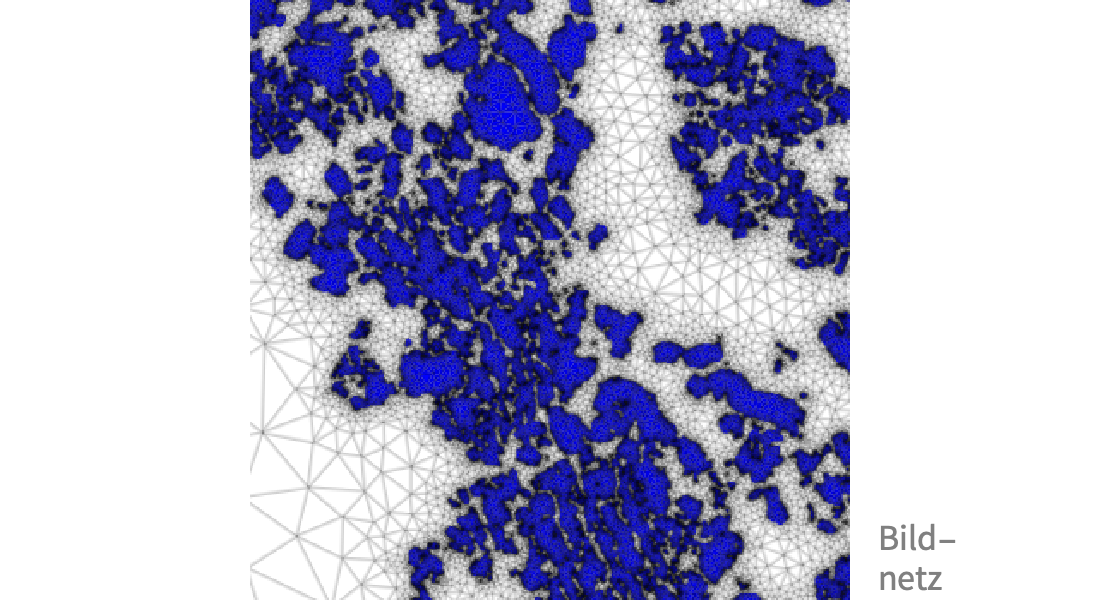
Gitternetze erzeugen
Für numerische Berechnungen können Sie Geometrien mit generierten oder importierten Meshes annähern. Legen Sie Verfeinerungen fest, erstellen Sie abgestufte oder gemappte Gitternetze und fügen Sie perfekt angepasste Schichten (PMLs) hinzu, die zu Ihrer Anwendung passen.
Wärmetransport
Berechnen Sie den Wärmetransport in multimateriellen, nichtlinearen, porösen, anisotropen Modellen mit Ereignissen oder Phasenänderungen in Flüssigkeiten oder Festkörpern. Verwenden Sie eine unterschiedliche Randbedingungen, PMLs und Quellenarten im ein-, zwei- oder dreidimensionalen Raum und für achsensymmetrische Fälle.
Fluiddynamik
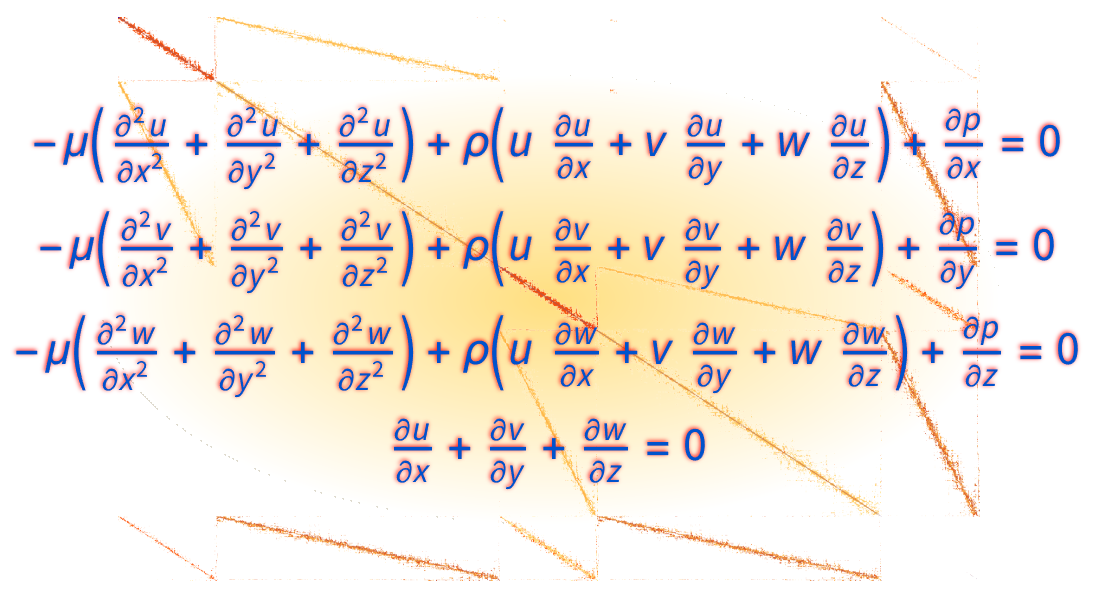
Analysieren Sie die Strömung von Flüssigkeiten. Lösen Sie die Stokes- oder Navier-Stokes-Gleichungen in 2 oder 3 Dimensionen. Modellieren Sie auftriebsgetriebene Strömungen mit der Boussinesq-Näherung oder koppeln Sie die Navier-Stokes-Gleichung mit anderen Bereichen der Physik wie Wärmeübertragung oder Stofftransport.
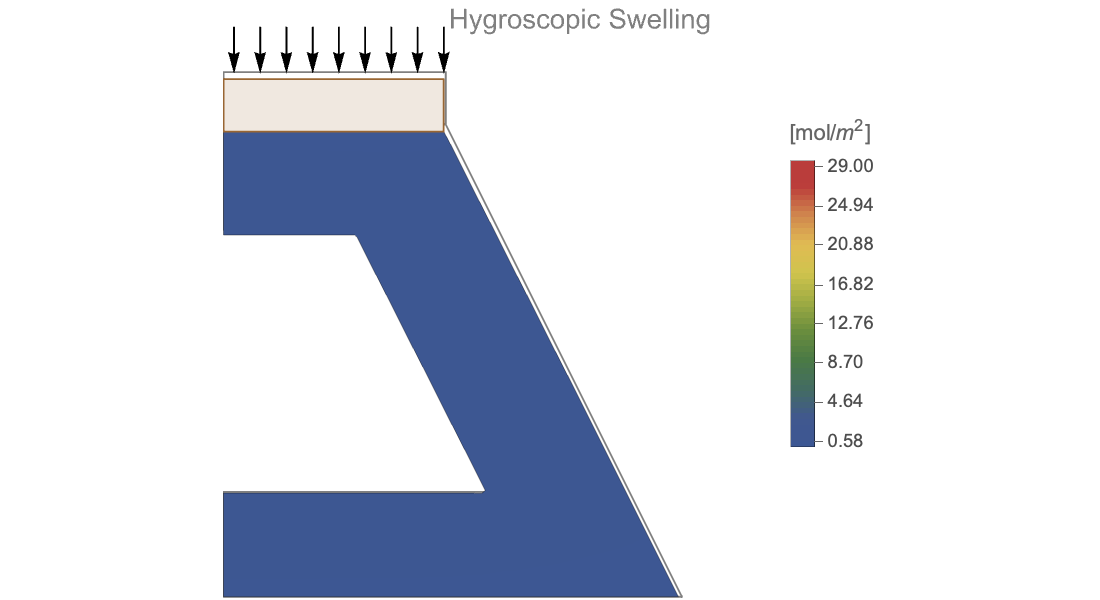
Massetransport
Modellieren Sie interphasigen oder anisotropen Stofftransport mit variablen, nichtlinearen Diffusionskoeffizienten einschließlich chemischer Reaktionen mit verschiedenen Quellen und Randbedingungen in einer, zwei oder drei Dimensionen und achsensymmetrischen Fällen.
Festkörpermechanik
Berechnen Sie Verschiebungen, Reaktionskräfte, Dehnungen und Spannungen. Verwenden Sie hyperelastische oder lineare und nichtlineare elastische, anisotrope Materialmodelle, eventuell gekoppelt mit Wärmeausdehnung. Führen Sie statische, zeitabhängige, parametrische, Frequenzgang-, Schwingungs- oder Eigenmodenanalysen in 2D und 3D durch.
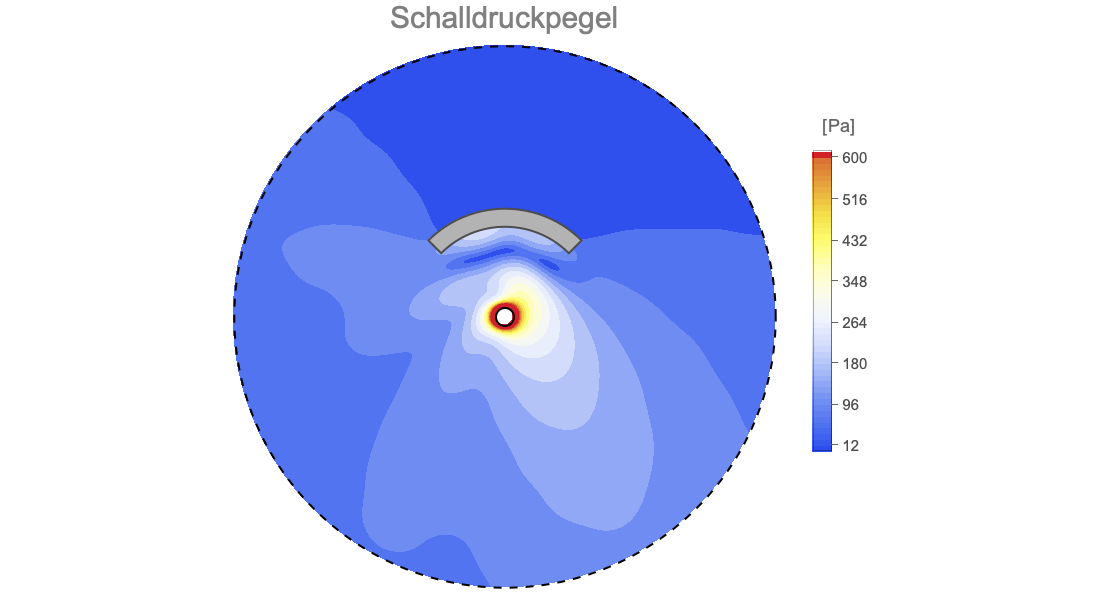
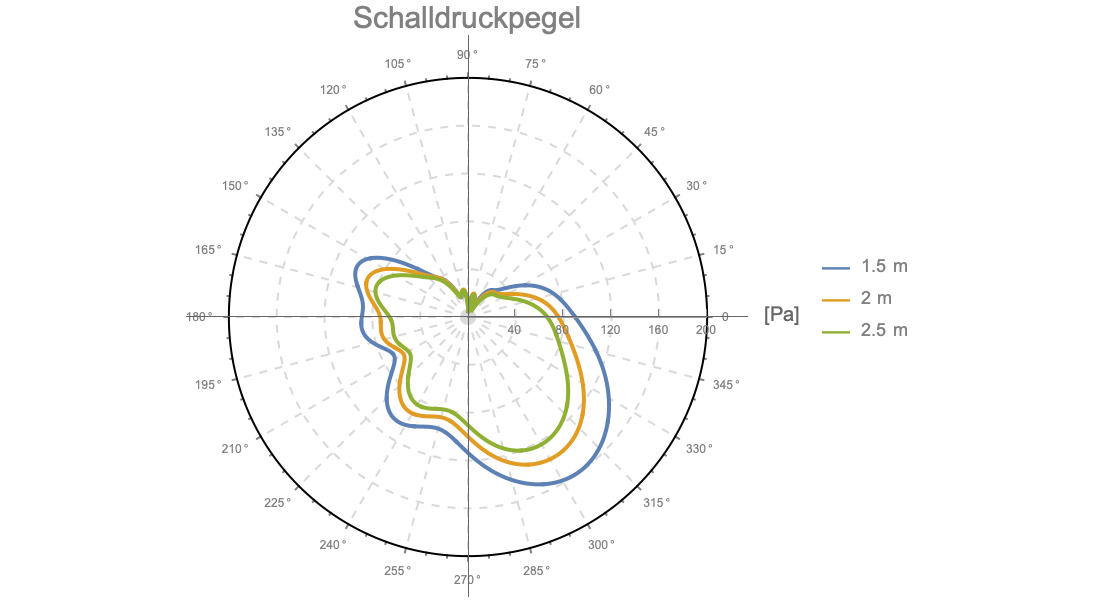
Akustik
Modellieren Sie die Multimaterial-Akustik im Zeit- oder Frequenzbereich. Führen Sie harmonische oder Eigenfrequenzanalysen mit einer Vielzahl von Randbedingungen und Quellen durch. Verwenden Sie PMLs, um genaue Lösungen zu erhalten. Hören Sie buchstäblich den Unterschied in Akustikmodellen.
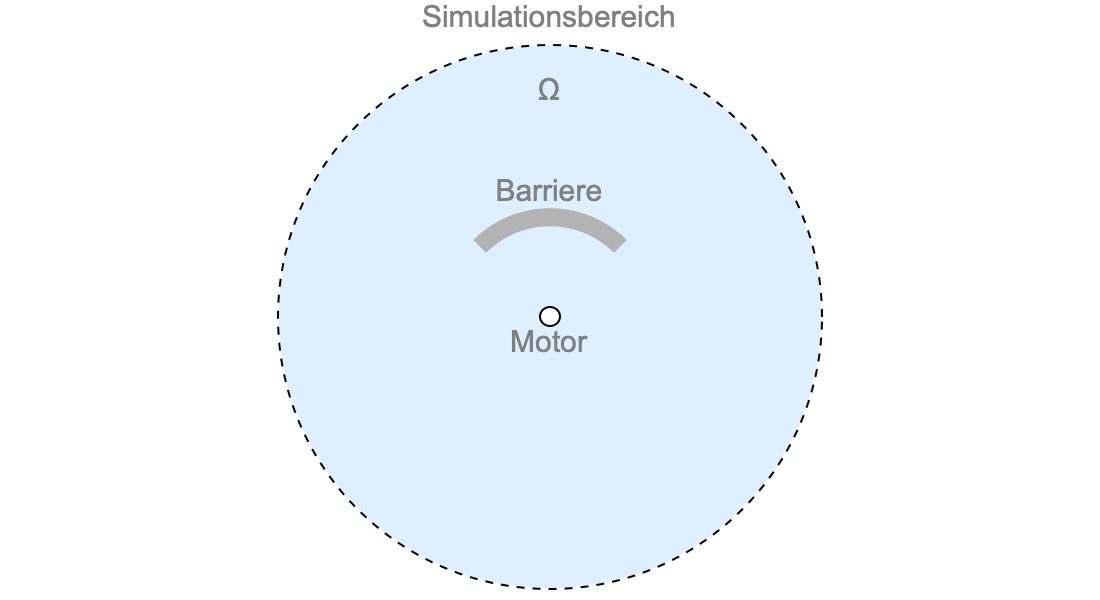
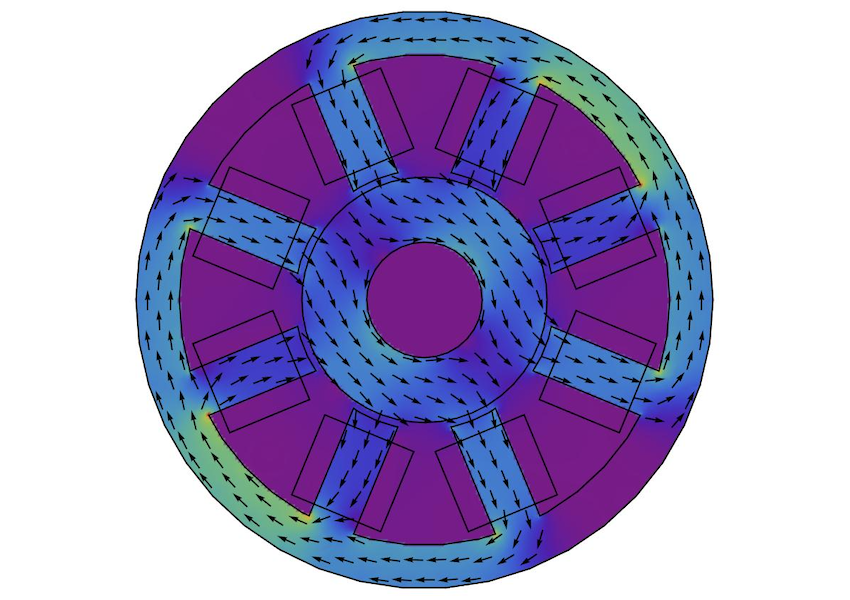
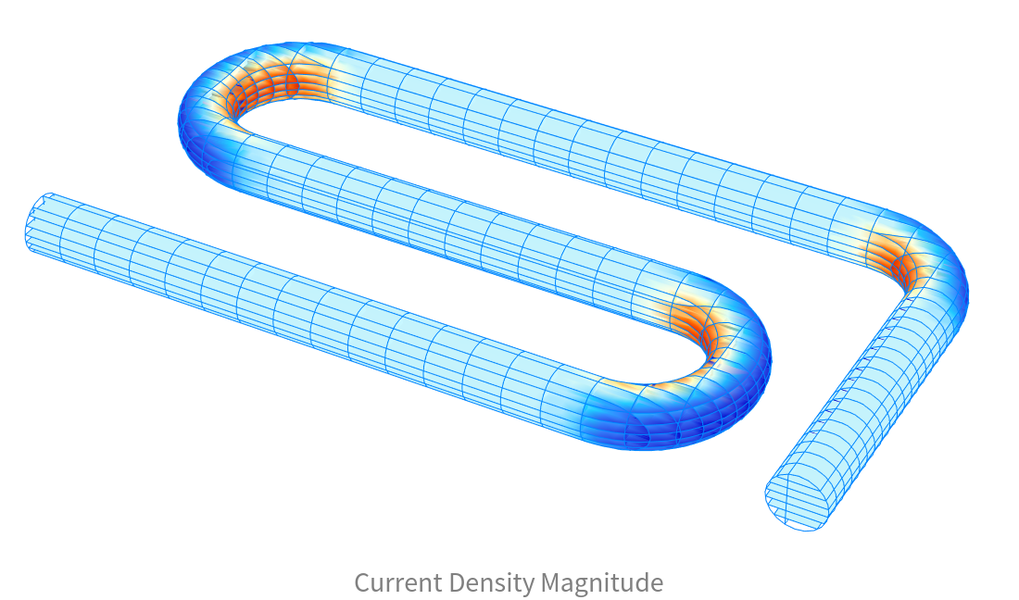
Elektromagnetik
Untersuchen und analysieren Sie elektromagnetische Geräte und lösen Sie die Maxwellschen Gleichungen. Modellieren Sie mit Elektrostatik, stationären Strömungen, Magnetostatik und elektromagnetischen Wellen in zwei oder drei Dimensionen, um Felder zu visualisieren oder sekundäre Größen wie Impedanz, Leistung und Verluste einfach zu berechnen.
Multiphysikalische Systeme
Kombinieren Sie vordefinierte physikalische Modelle, ohne Add-on-Pakete zu kaufen. Denken Sie die Analyse mit der Finite-Elemente-Methode neu, indem Sie die PDG-basierte Analyse mit den Wolfram-Funktionen für Bildverarbeitung, Geographie, Chemie oder Signal kombinieren. Erstellen Sie Modellkoeffizienten aus Echtzeit-Sensordaten oder greifen Sie auf kuratierte Daten aus einer großen Anzahl von Themen zu.
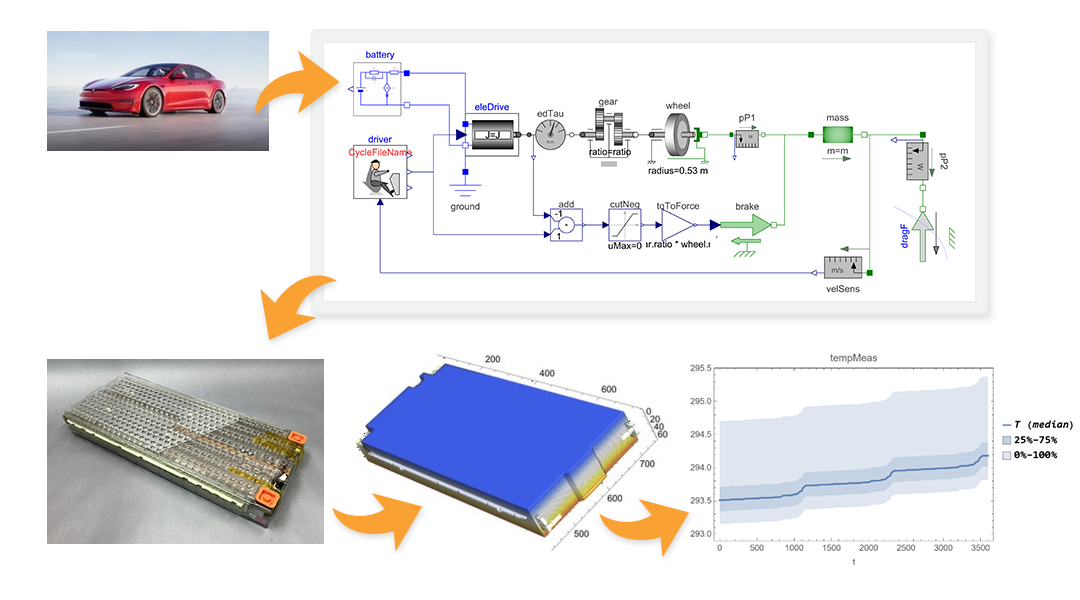
Systemphysik
Kombinieren Sie mit System Modeler Finite-Elemente-Modelle. Verwenden Sie PDG-Modelle zur Steuerung von Systemmodellen oder wandeln Sie Modelle in PDGs um. Modellieren Sie jede Komponente in einem komplexen System auf der entsprechenden Ebene.
Integrierte Nachbearbeitung
Nie mehr unzureichendes Nachbearbeiten von Lösungen! Erstellen Sie gestochen scharfe Visualisierungen, berechnen Sie Farbverläufe oder integrieren Sie Ihre Lösungen - alles in derselben Arbeitsumgebung.

Solver für Gleichungen
Führen Sie nichtlineare, stationäre oder zeitabhängige Analysen mit speziellen, vielseitigen iterativen und parallelen, direkten oder Out-of-Core-Solvern sowie einem Eigenmode-Solver und einem parametrischen Solver durch. Keine Beschränkung in der Anzahl der verwendeten Knoten oder Elemente. Nichtlineare PDGs werden automatisch linearisiert.
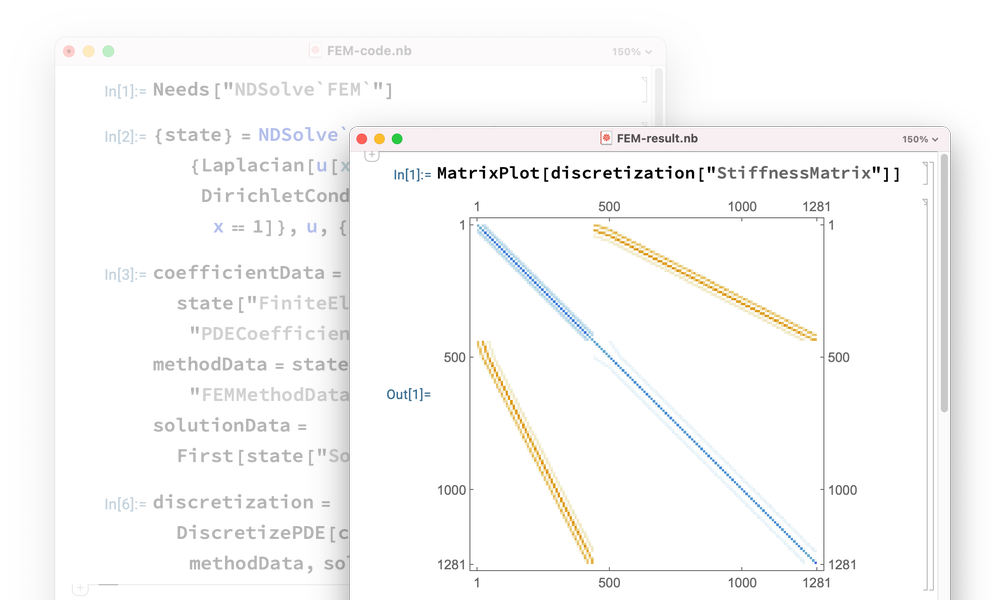
FEM programmieren mit einer API
Sie können jeden Aspekt des FEM-Lösungsprozesses in jeder Phase abfangen und kontrollieren und sogar neue Algorithmen für die Lösung von PDEs entwickeln.
Dokumentation für Wolfram FEM
Wolfram FEM ist integrierter Bestandteil der Wolfram Language. Das vollständige System enthält über 6.000 eingebaute Funktionen, die alle Bereiche des Rechnens abdecken—alle sorgfältig integriert, damit sie perfekt zusammenarbeiten.

Vollständiger Umfang & Dokumentation