WolframMEFUn élément essentiel de
Wolfram Language

Méthode des éléments finis.

Pour les débutants comme pour les experts, la MEF avec Wolfram permet de saisir le comportement de votre conception en fournissant des modèles d'équations différentielles partielles multi-physiques, des solveurs et des fonctions de post-traitement transparentes, entièrement intégrés à des capacités avancées de géométrie et de visualisation.

Démarrer

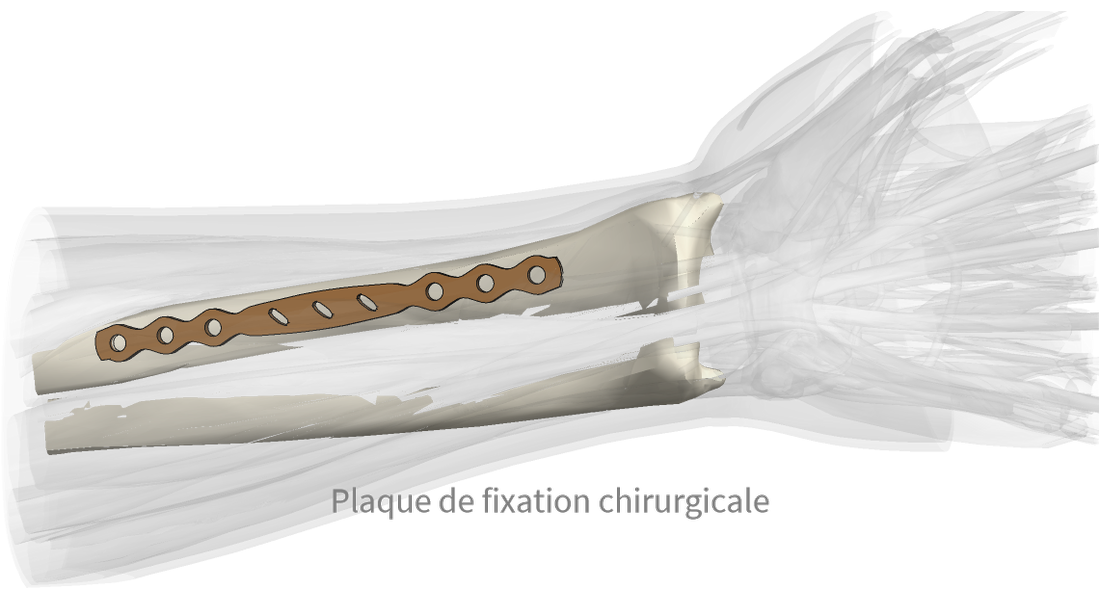
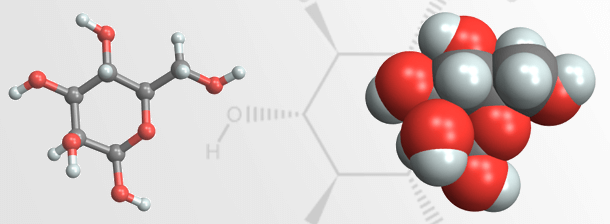
Modélisation géométrique

Concevez des simulations précises. Créez des modèles géométriques multi-matériaux à l'aide d'opérations booléennes ou de descriptions implicites, ou reconstruisez-les à partir de données ponctuelles, d'images, de cartes géographiques, etc. Importez de nombreux formats de fichiers CAO et autres formats de fichiers géométriques tels que STEP, DXF et STL.

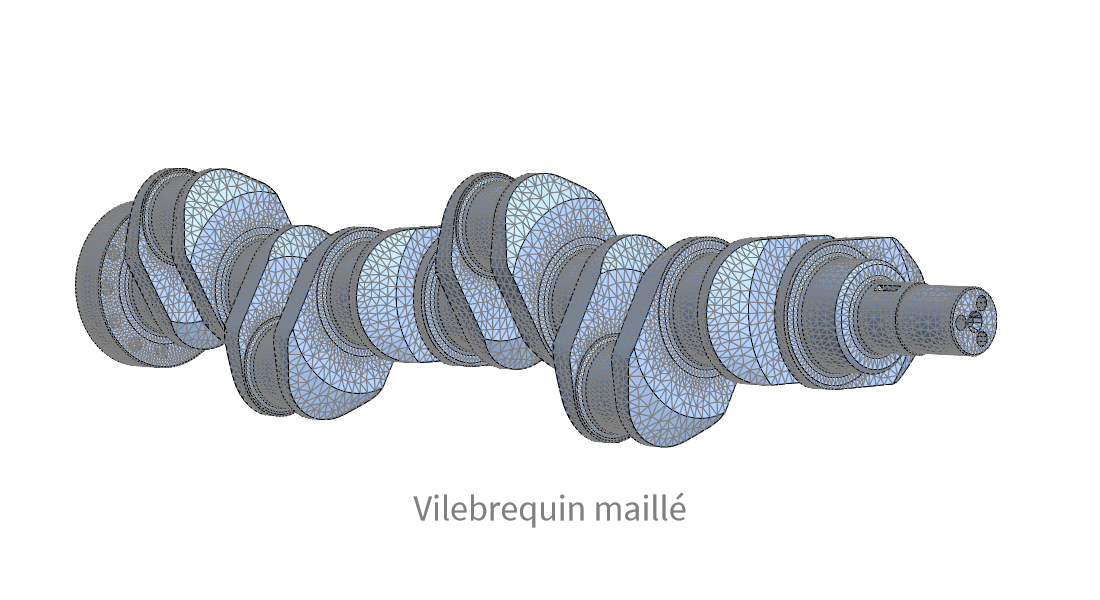
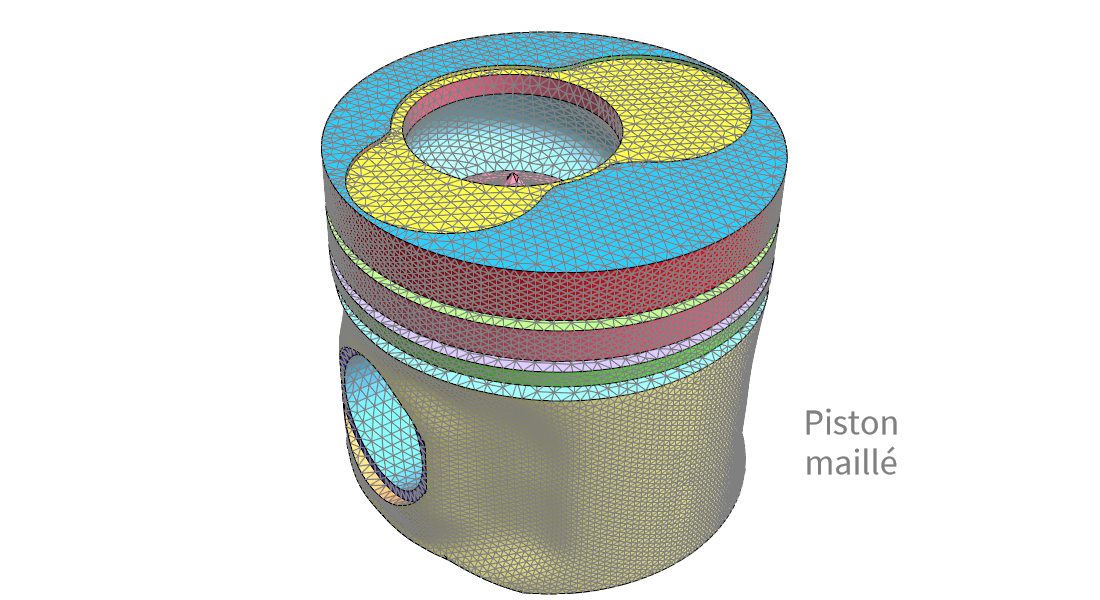
Génération de mailles

Pour le calcul numérique, rapprochez les géométries à l'aide de mailles générées ou importées. Spécifiez des raffinements, créez des mailles graduées ou cartographiées, et ajoutez des couches parfaitement adaptées (PML) pour les intégrer à votre application.

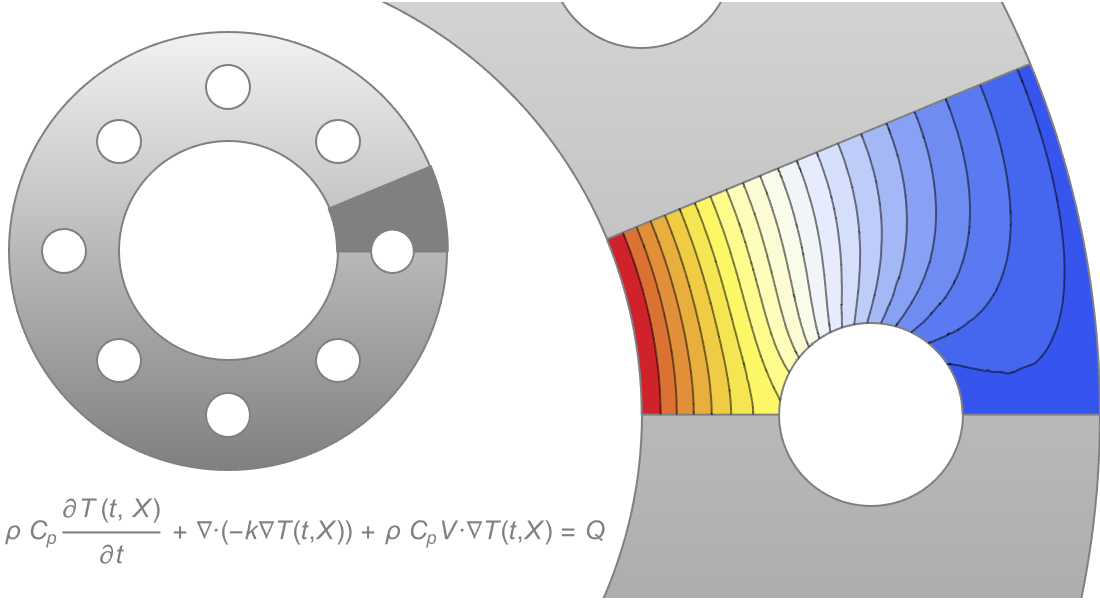
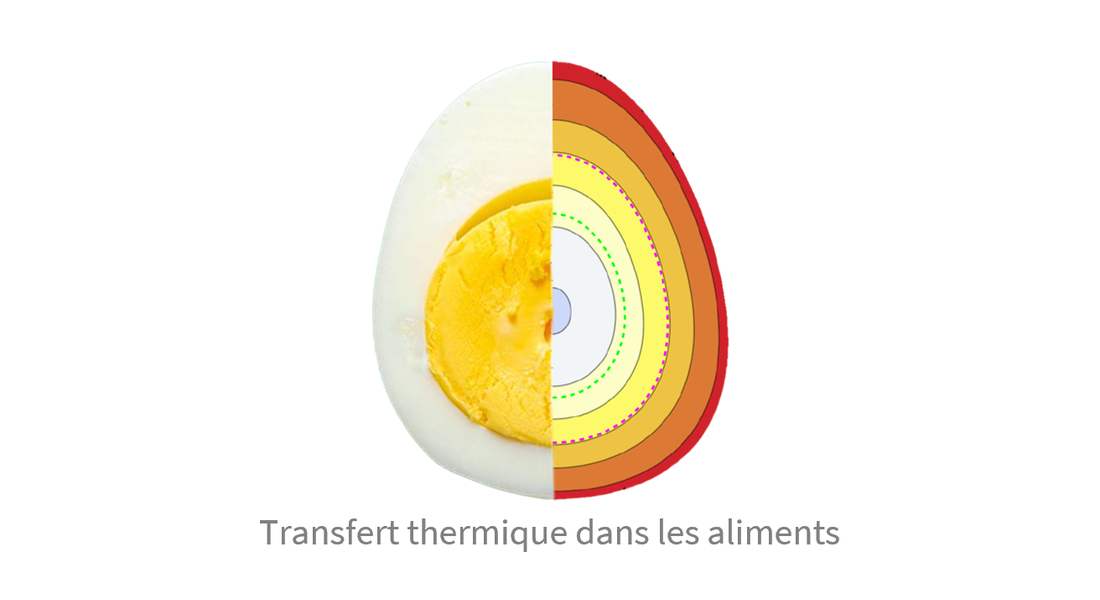
Transfert de chaleur

Calculez le transfert de chaleur dans des modèles multi-matériaux, non linéaires, poreux, anisotropes avec des événements ou des changements de phase dans les fluides ou les solides. Utilisez une variété de conditions aux limites, de PML et de types de sources pour les cas 1D, 2D, 3D et axisymétriques.

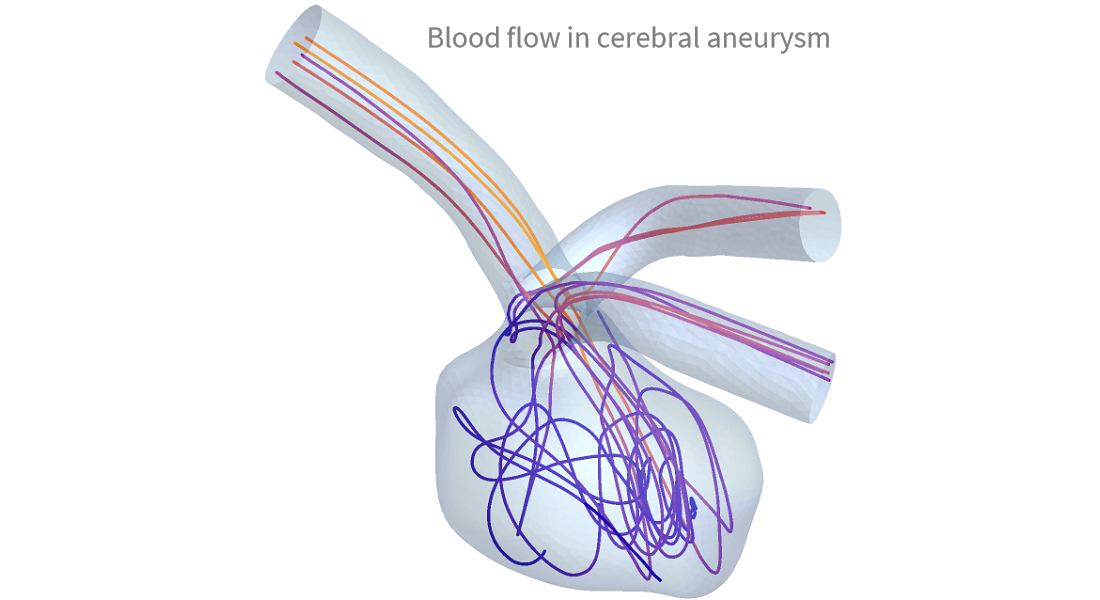
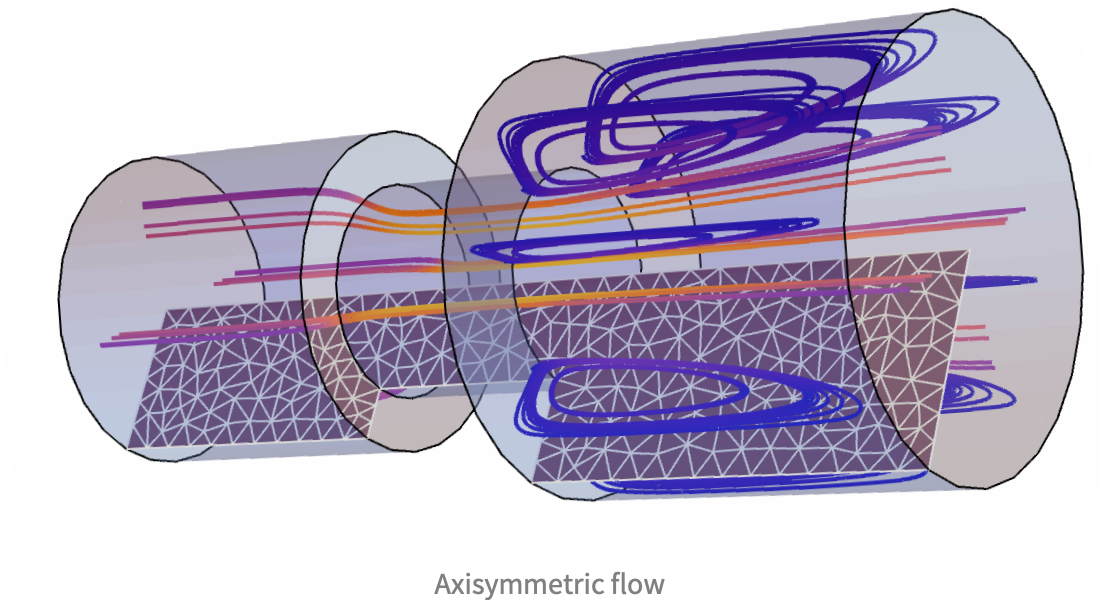
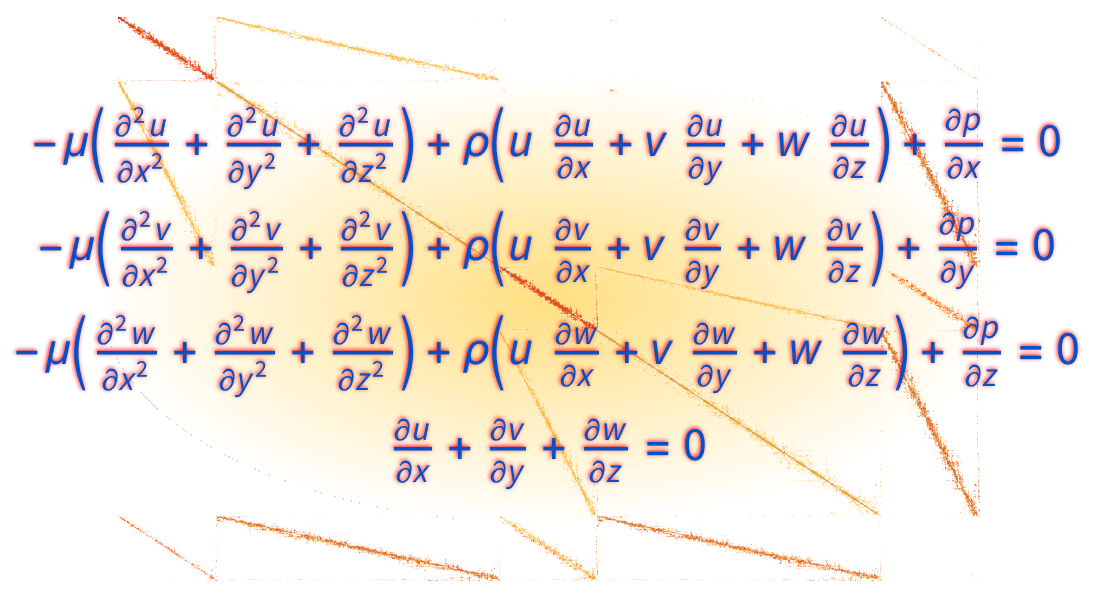
Dynamique des fluides

Analysez l'écoulement des fluides. Résolvez les équations de Stokes ou de Navier–Stokes en 2 ou 3 dimensions. Modélisez les écoulements induits par la flottabilité avec l'approximation de Boussinesq ou combinez l'équation de Navier–Stokes à d'autres domaines de la physique tels que le transfert de chaleur ou le transport de masse.

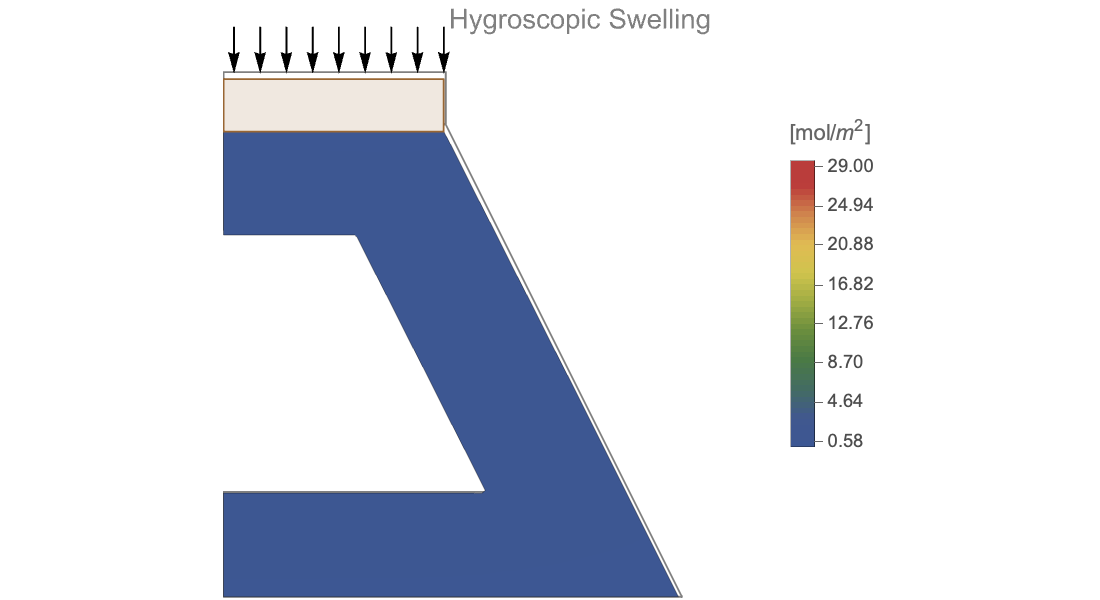
Transport de masse

Modélisez le transport de masse interphase ou anisotrope avec des coefficients de diffusion variables et non linéaires, y compris les réactions chimiques avec diverses sources et conditions aux limites dans les cas 1D, 2D, 3D et axisymétriques.

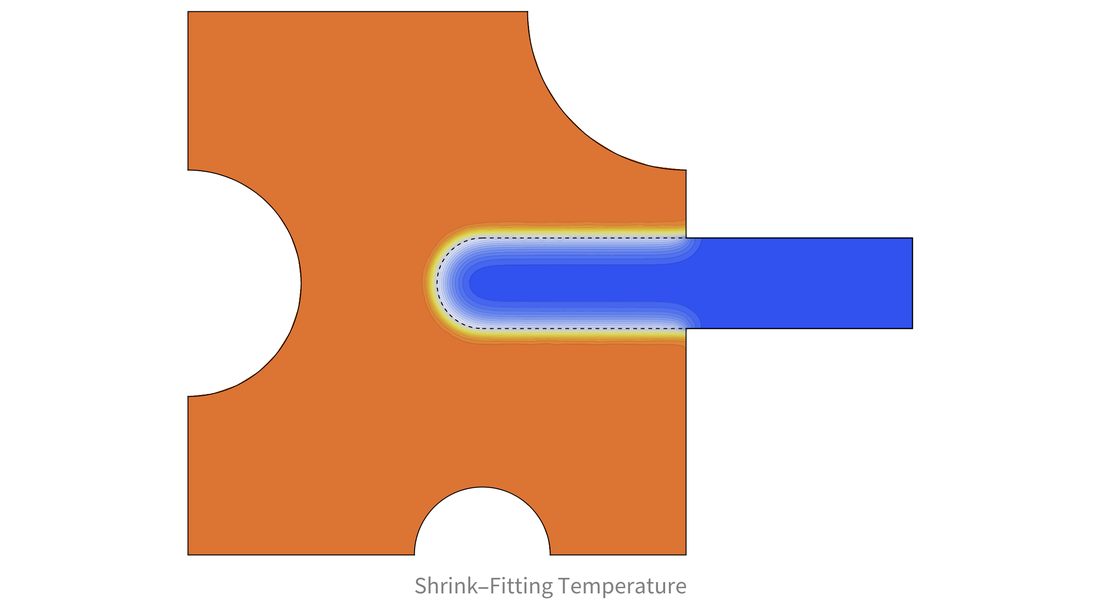
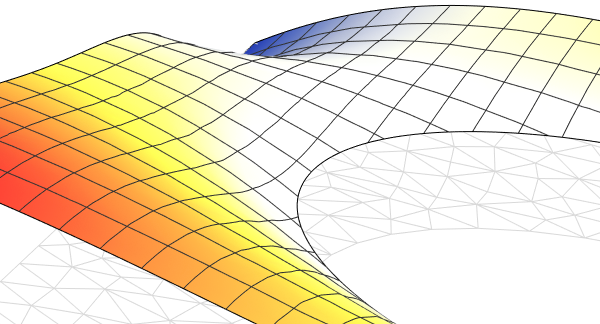
Mécanique des solides

Calculez les déplacements, les forces de réaction, les déformations et les contraintes. Utilisez des modèles de matériaux hyperélastiques ou élastiques linéaires et non linéaires, anisotropes, éventuellement combinés à une dilatation thermique. Effectuez des analyses statiques, temporelles, paramétriques, de réponse en fréquence, de vibrations ou de modes propres en 2D et en 3D.

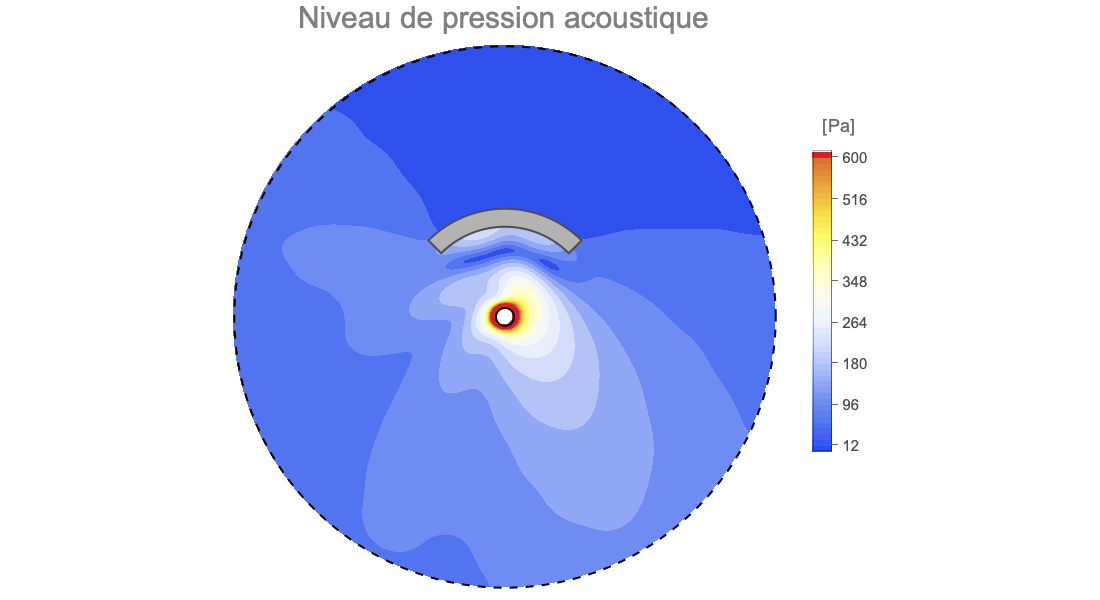
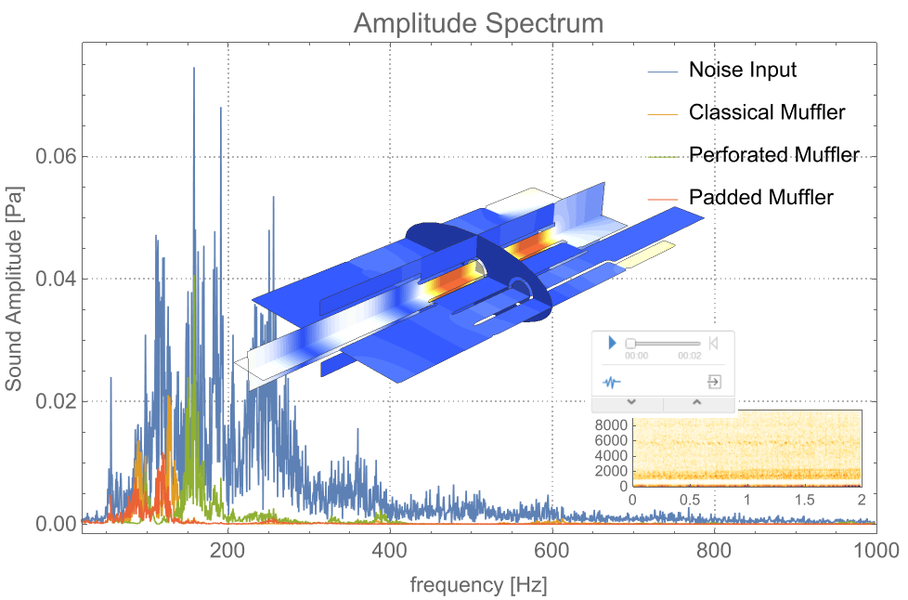
Acoustique

Modélisez l'acoustique multi-matériaux dans le domaine temporel ou fréquentiel. Effectuez des analyses harmoniques ou de fréquences propres avec une multitude de conditions aux limites et de sources. Utilisez les PML pour obtenir des solutions précises. Entendez réellement la différence dans les conceptions acoustiques.

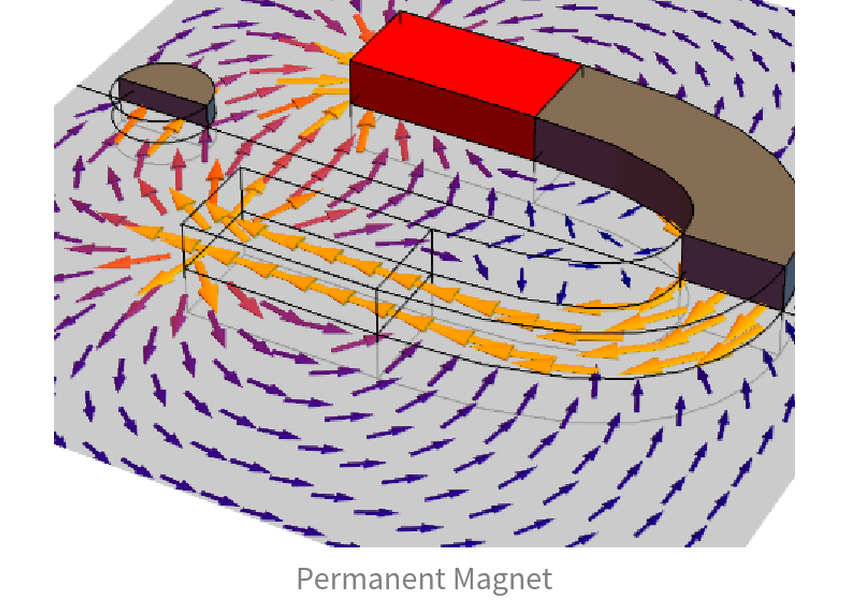
Électromagnétisme

Explorez et analysez les dispositifs électromagnétiques, en résolvant les équations de Maxwell. Réalisez des modèles avec l'électrostatique, les courants continus, la magnétostatique et les ondes électromagnétiques en 2 ou 3 dimensions afin de visualiser les champs ou de calculer facilement des quantités secondaires telles que l'impédance, la puissance et les pertes.

Multiphysique

Combinez des modèles physiques prédéfinis sans acheter de progiciels supplémentaires. Repensez la FEA en combinant l'analyse des EDP avec l'image, la géographie, la chimie ou le signal selon Wolfram. Définissez les coefficients du modèle à partir de données de capteurs en temps réel ou accédez à des données référencées à partir d'un vaste ensemble de sujets.

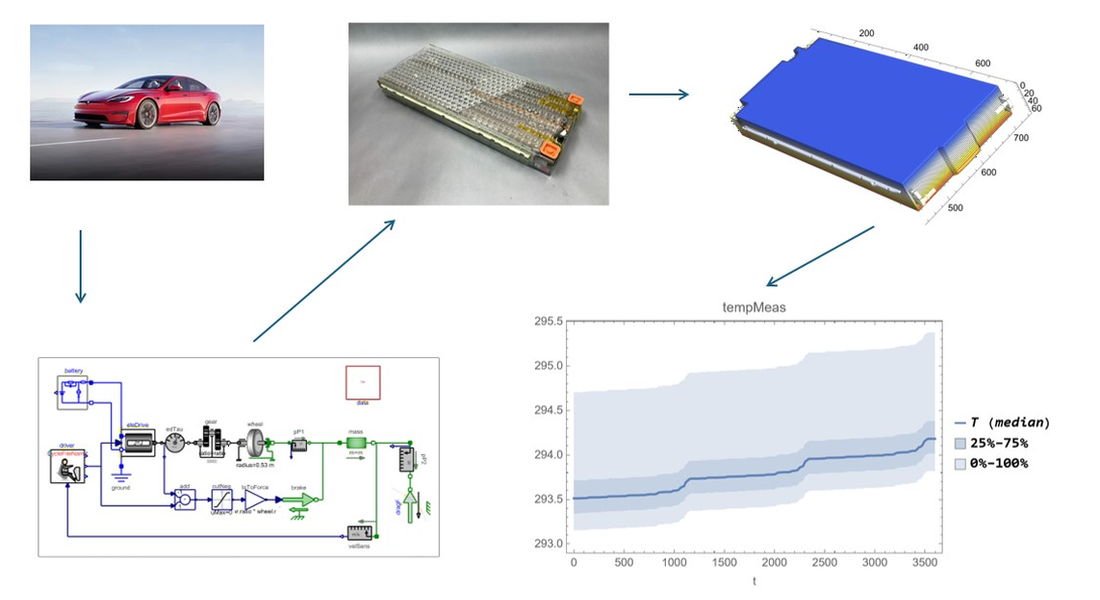
Guide pour les exemples multiphysiques

Physique du système

Combinez des modèles d'éléments finis avec System Modeler. Utilisez les modèles d'EDP pour piloter les modèles du système et vice-versa. Modélisez chaque composante d'un système complexe à son niveau approprié.

Post-traitement intégré

Débarrassez vos solutions d'un post-traitement médiocre. Produisez des visualisations nettes, calculez des gradients ou intégrez vos solutions, le tout dans le même environnement de travail.

Solveurs d'équations

Effectuez des analyses non linéaires, stationnaires ou dépendantes du temps avec des solveurs itératifs et parallèles, directs ou hors cœur, dédiés et polyvalents, ainsi qu'un solveur de modes propres et un solveur paramétrique. Aucune restriction quant au nombre de nœuds ou d'éléments utilisés. Les EDP non linéaires sont automatiquement linéarisées.

API de programmation de la MEF

Interceptez et contrôlez chaque aspect du processus de résolution de la MEF à n'importe quel stade, et concevez même de nouveaux algorithmes pour résoudre les EDP.

Live Playground

This is an interactive notebook—try making your own changes!

Continue exploring more examples:Things to Try

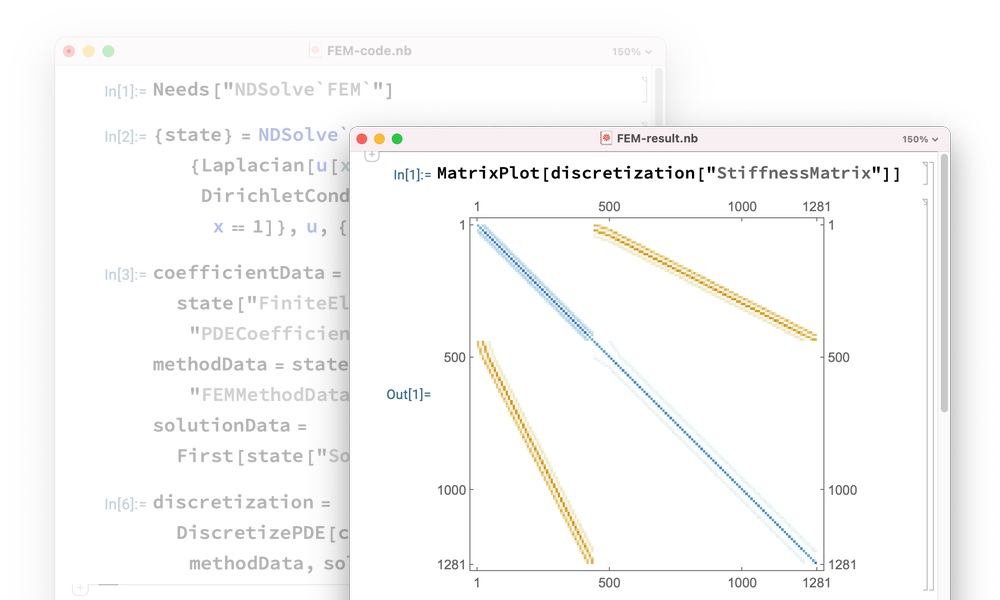
Documentation de Wolfram MEF

Wolfram MEF fait partie intégrante de Wolfram Language. Le système complet contient plus de 6000 fonctions intégrées couvrant tous les domaines du calcul, toutes soigneusement intégrées pour fonctionner parfaitement ensemble.

Wolfram Language
Champ d'application et documentation

Guide

Modélisation des EDP

Overview

Aperçu des modèles d'EDP

Tech Note

Résolution d'EDP avec la MEF

D ▪ Derivative ▪ Grad ▪ Div ▪ Curl ▪ Laplacian ▪ NDSolve ▪ DSolve ▪ NDSolveValue ▪ ParametricNDSolve ▪ NDEigensystem ▪ NDEigenvalues ▪ NIntegrate ▪ DirichletCondition ▪ NeumannValue ▪ PeriodicBoundaryCondition ▪ AcousticPDEComponent ▪ AcousticAbsorbingValue ▪ AcousticImpedanceValue ▪ AcousticNormalVelocityValue ▪ AcousticPressureCondition ▪ AcousticRadiationValue ▪ AcousticSoundHardValue ▪ AcousticSoundSoftCondition ▪ HeatTransferPDEComponent ▪ HeatFluxValue ▪ HeatInsulationValue ▪ HeatOutflowValue ▪ HeatRadiationValue ▪ HeatTemperatureCondition ▪ HeatSymmetryValue ▪ HeatTransfreValue ▪ MassConcentrationCondition ▪ MassFluxValue ▪ MassImpermeableBoundaryValue ▪ MassOutflowValue ▪ MassSymmetryValue ▪ MassTransportPDEComponent ▪ MassTransferValue ▪ SolidMechanicsPDEComponent ▪ SolidMechanicsStrain ▪ SolidMechanicsStress ▪ SolidBoundaryLoadValue ▪ SolidDisplacementCondition ▪ SolidFixedCondition ▪ LaplacianPDETerm ▪ PoissonPDEComponent ▪ WavePDEComponent ▪ DiffusionPDETerm ▪ ConvectionPDETerm ▪ ReactionPDETerm ▪ SourcePDETerm ▪ DerivativePDETerm ▪ ConservativeConvectionPDETerm ▪ Line ▪ DiscretizedPDEData ▪ DiscretizedBoundaryConditionData ▪ LinearSolve ▪ FunctionExpand ▪ DifferentialRootReduce ▪ RegionNearest ▪ RegionMeasure ▪ RegionCentroid ▪ RegionDistance ▪ Region ▪ CanonicalizeRegion ▪ Ball ▪ Simplex ▪ Hexahedron ▪ InfiniteLine ▪ CrossingPolygon ▪ RandomPolygon ▪ PolygonDecomposition ▪ Polyhedron ▪ Dodecahedron ▪ Icosahedron ▪ DualPolyhedron ▪ HighlightMesh ▪ MeshCellStyle ▪ MeshCellLabel ▪ RegionUnion ▪ TransformedRegion ▪ RegionIntersection ▪ BooleanRegion ▪ RegionBoundary ▪ DelaunayMesh ▪ VoronoiMesh ▪ ConvexHullMesh ▪ ArrayMesh ▪ ImageMesh ▪ RegionConvert ▪ DiscretizeGraphics ▪ BoundaryDiscretizeGraphics ▪ DiscretizeRegion ▪ BoundaryDiscretizeRegion ▪ PolyhedronData ▪ ExampleData ▪ GeoElevationData ▪ ChemicalData ▪ AnatomyData ▪ KnotData ▪ LaminaData ▪ SolidData ▪ PlaneCurveData ▪ SpaceCurveData ▪ SurfaceData ▪ Printout3D ▪ FindMeshDefects ▪ RepairMesh ▪ ShellRegion ▪ GeometricScene ▪ RandomInstance ▪ FindGeometricConjectures ▪ ElectricCurrentPDEComponent ▪ ElectricCurrentDensityValue ▪ Polygon ▪ DensityPlot ▪ VonMisesStress ▪ IdentityMatrix ▪ TransformationFunction ▪ TranslationTransform ▪ HoldAll ▪ Block ▪ Exclusions ▪ ParametricRegion ▪ BoundaryMeshRegion ▪ MaxRecursion ▪ Interpolation ▪ Quantile ▪ BesselJ ▪ EllipticE ▪ CDF ▪ NMinimize ▪ NSum ▪ AsymptoticIntegrate ▪ NLineIntegrate ▪ NSurfaceIntegrate ▪ NContourIntegrate ▪ NExpectation ▪ NProbability ▪ ArcLength ▪ Area ▪ Volume ▪ MomentOfInertia ▪ Eigenvalues ▪ Sort ▪ Eigensystem ▪ Indeterminate ▪ MaxCellMeasure ▪ SortBy ▪ ImplicitRegion ▪ Reals ▪ Complexes ▪ Element ▪ ParametricFunction ▪ SystemModelParametricSimulate ▪ ParametricNDSolveValue ▪ Vectors ▪ Matrices ▪ $Assumptions ▪ DiscreteVariables ▪ GeneratedParameters ▪ WeierstrassP ▪ Erf ▪ C ▪ Assumptions ▪ IncludeSingularSolutions ▪ ParametricPlot ▪ FinancialDerivative ▪ InverseLaplaceTransform ▪ Activate ▪ DSolveValue ▪ DFixedPoints ▪ DStabilityConditions ▪ GreenFunction ▪ CompleteIntegral ▪ RSolve ▪ TruncateSum ▪ WhenEvent ▪ Compiled ▪ EvaluationMonitor ▪ StartingStepSize ▪ StepMonitor ▪ None ▪ MachinePrecision ▪ NormFunction ▪ Infinity ▪ WorkingPrecision ▪ MaxSteps ▪ DependentVariables ▪ Automatic ▪ Method ▪ Disk ▪ InterpolationOrder ▪ All ▪ MaxStepFraction ▪ MaxStepSize ▪ Sign ▪ Abs ▪ SystemModel ▪ AccuracyGoal ▪ PrecisionGoal ▪ AsymptoticDSolveValue ▪ NSolve ▪ DifferentialRoot ▪ StreamPlot ▪ SystemModelSimulate ▪ ItoProcess ▪ SymbolicZerosArray ▪ Cross ▪ TensorExpand ▪ Listable ▪ TensorContract ▪ Dot ▪ DEigenvalues ▪ SymbolicIdentityArray ▪ Transpose ▪ CoordinateChartData ▪ NetPortGradient ▪ Residue ▪ VectorSymbol ▪ MatrixSymbol ▪ ArraySymbol ▪ NonConstants ▪ Gamma ▪ PolyGamma ▪ AiryAiPrime ▪ AiryBiPrime ▪ Zeta ▪ JacobiSN ▪ JacobiCD ▪ LogIntegral ▪ ExpIntegralEi ▪ SinIntegral ▪ ConditionalExpression ▪ RealAbs ▪ RealSign ▪ Floor ▪ Ceiling ▪ Equal ▪ SymmetrizedArray ▪ SparseArray ▪ FourierTransform ▪ ZTransform ▪ GeneratingFunction ▪ KroneckerDelta ▪ GammaDistribution ▪ EstimatedDistribution ▪ Limit ▪ N ▪ First ▪ Outer ▪ Join ▪ Dimensions ▪ HodgeDual ▪ Total ▪ ArcCurvature ▪ DEigensystem ▪ DiscreteShift ▪ Solve ▪ Piecewise ▪ Sin ▪ Dt ▪ DifferenceQuotient ▪ Minimize ▪ Maximize ▪ Integrate ▪ DifferenceDelta ▪ CoefficientArrays ▪ FractionalD ▪ CaputoD ▪ ImplicitD ▪ RegionQ ▪ False ▪ RegionPlot ▪ RegionPlot3D ▪ True ▪ FindGeometricTransform ▪ MeshRegion ▪ InitialSeeding ▪ InterpolatingFunction ▪ Plot3D ▪ Animate ▪ Inactivate ▪ Inactive ▪ HelmholtzPDEComponent ▪ SchrodingerPDEComponent ▪ ElectrostaticPDEComponent ▪ ElectricPotentialCondition ▪ ElectricFluxDensityValue ▪ ElectricSymmetryValue ▪ FluidFlowPDEComponent ▪ HeatTransferValue ▪