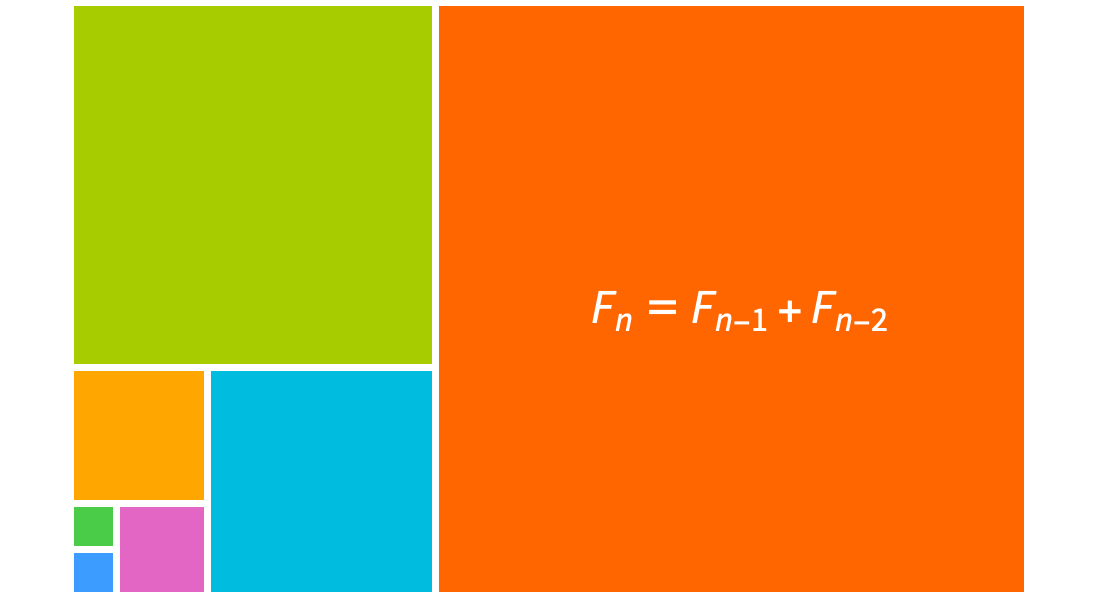WolframFunciones matemáticasUna parte fundamental de
Wolfram Language

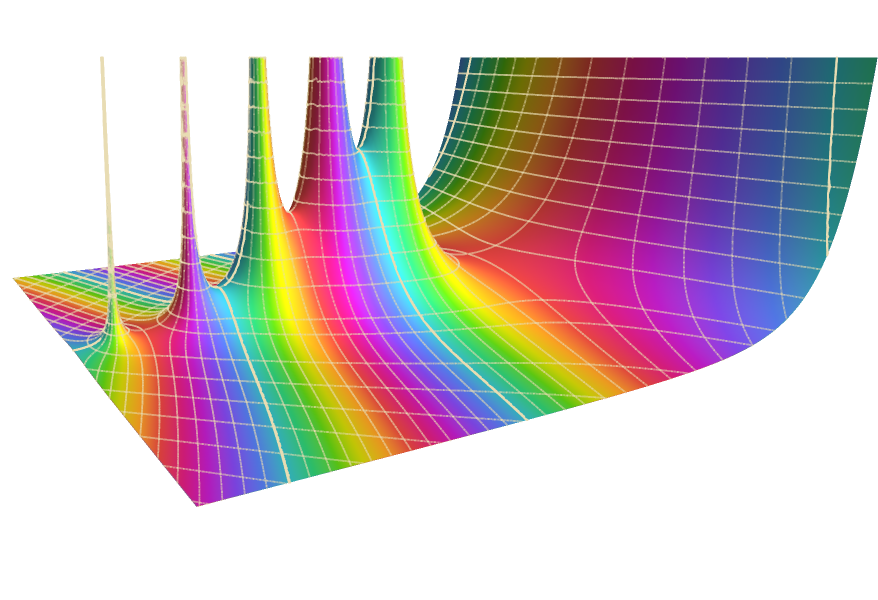
Defina, calcule y visualice.

Evaluación simbólica y numérica, visualización y expansiones asintóticas de una amplia colección de funciones matemáticas, extensamente documentadas e integradas estrechamente con todas las áreas de Wolfram Language.

Comenzar

Colección más completa

Con cientos de funciones especiales desde elementales hasta avanzadas, esta amplia colección está sólidamente integrada en solucionadores simbólicos y numéricos. Calcule resultados numéricos con la precisión deseada y encuentre o simplifique fórmulas. La documentación extensa, multinivel e interactiva permite a cualquier persona aprovechar su potencial.

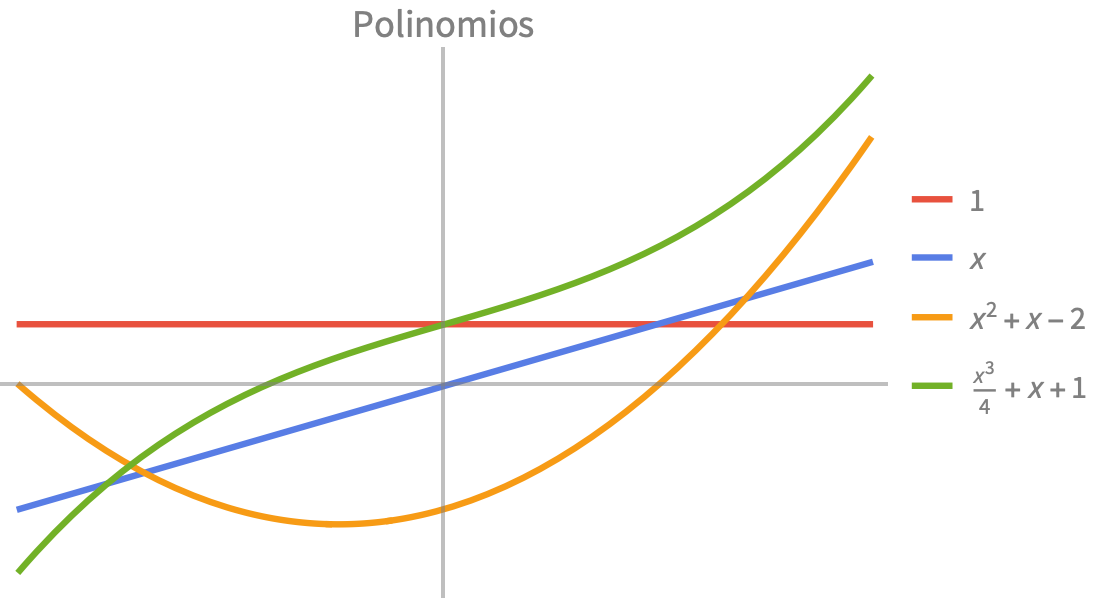
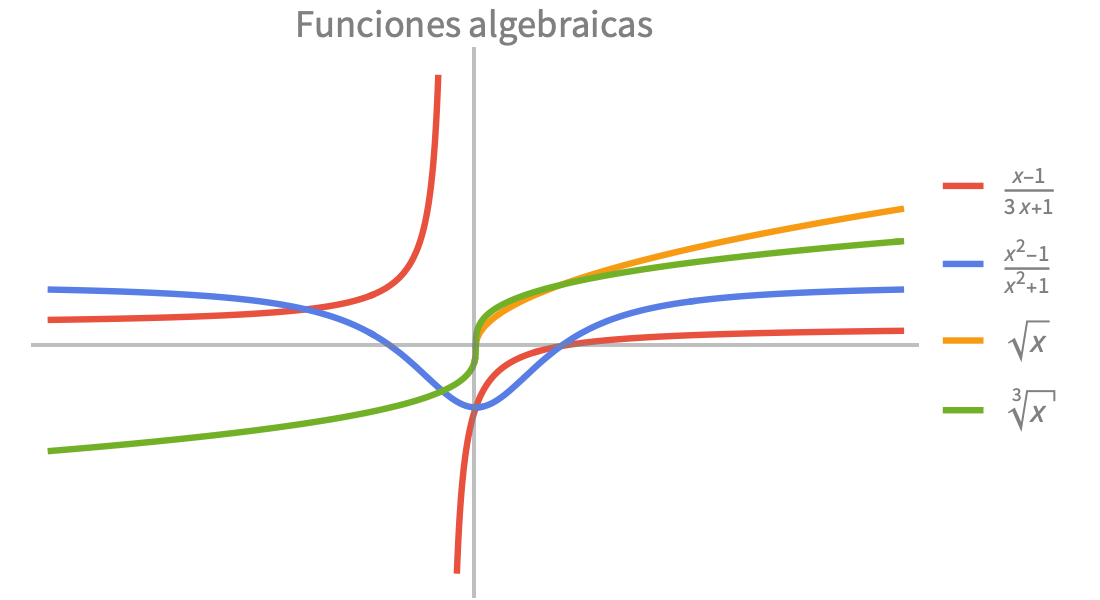
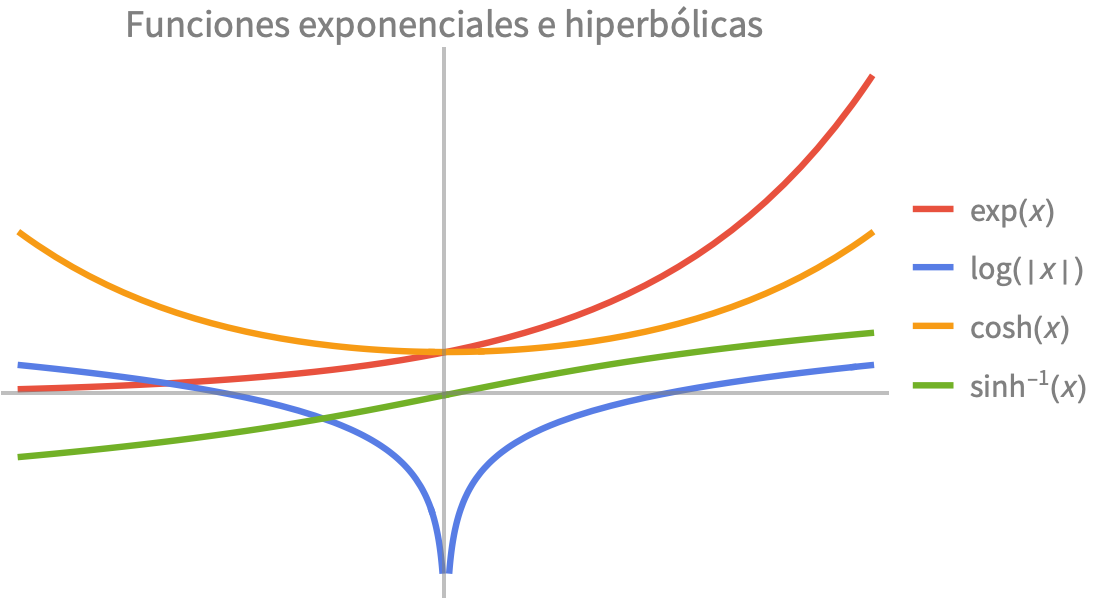
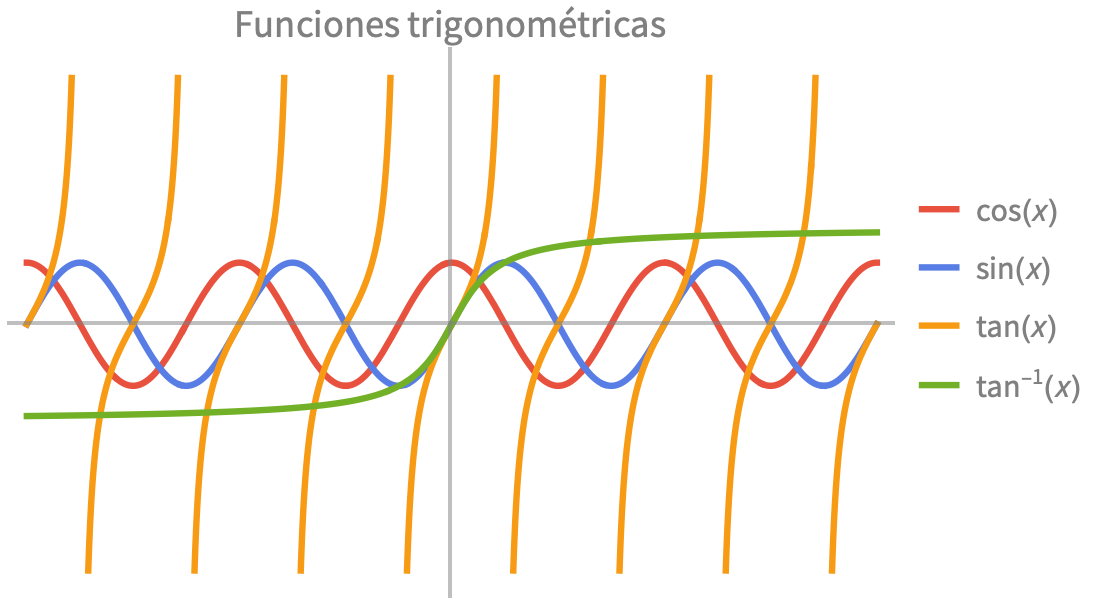
Funciones elementales

Cálculos numéricos y simbólicos rápidos y precisos para aplicaciones científicas y de ingeniería. Funciones exponenciales, trigonométricas e hiperbólicas incorporadas para modelar combinaciones de crecimiento, decaimiento y comportamiento oscilatorio.

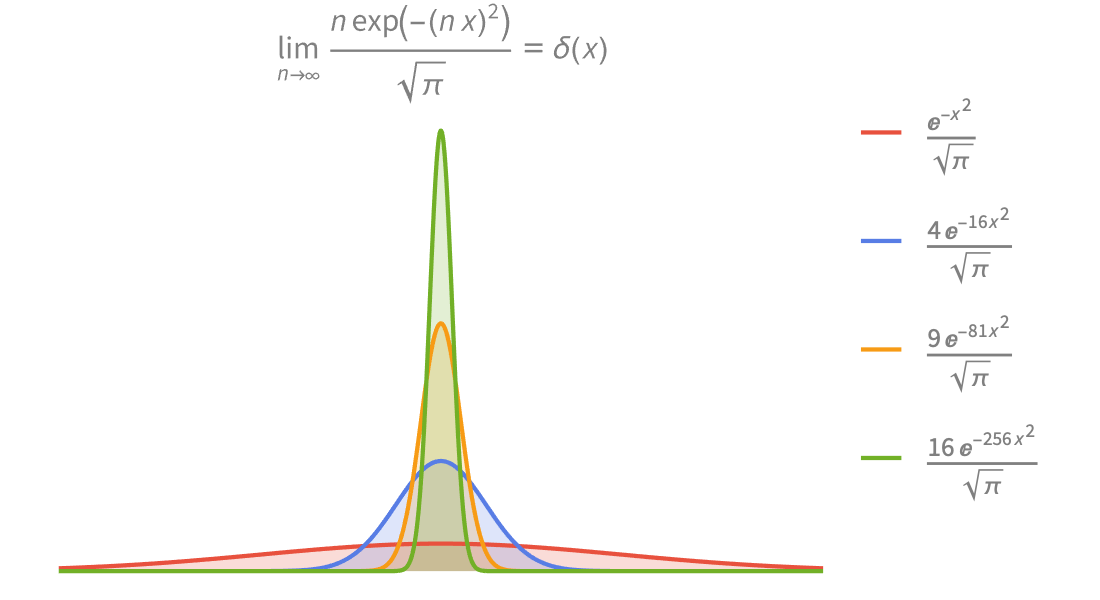
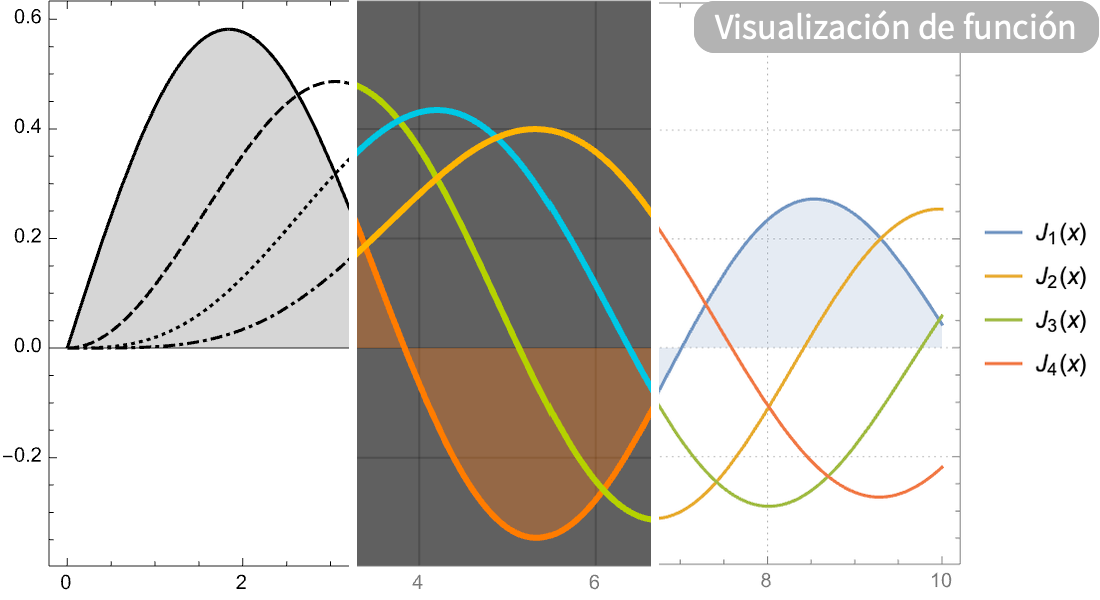
Funciones especiales

Resuelva problemas de física, ingeniería, probabilidad y estadística con numéricos de alta precisión o mediante expansiones simbólicas en serie.

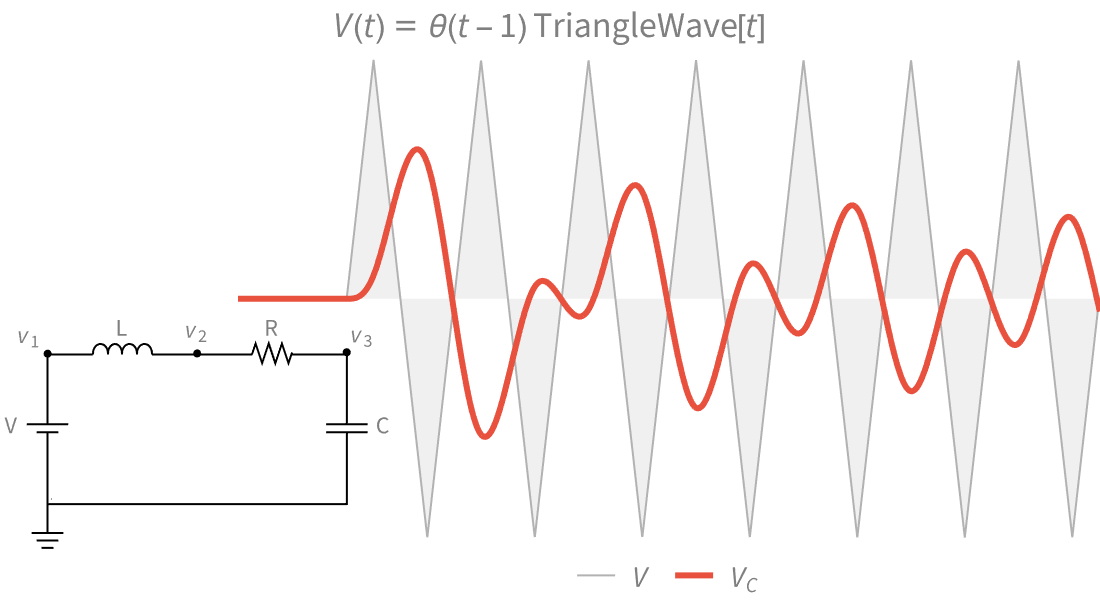
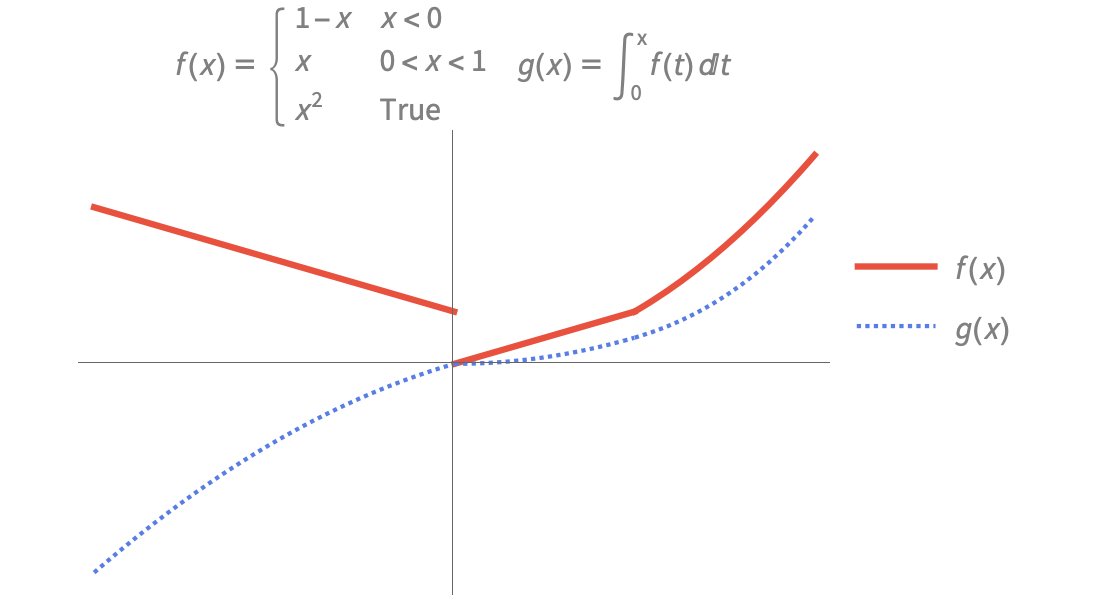
Funciones generalizadas y a trozos

Modele sistemas físicos y de ingeniería con un rango completo de funciones a trozos definidas punto por punto y funciones generalizadas. Construya sus propias funciones mediante Piecewise.

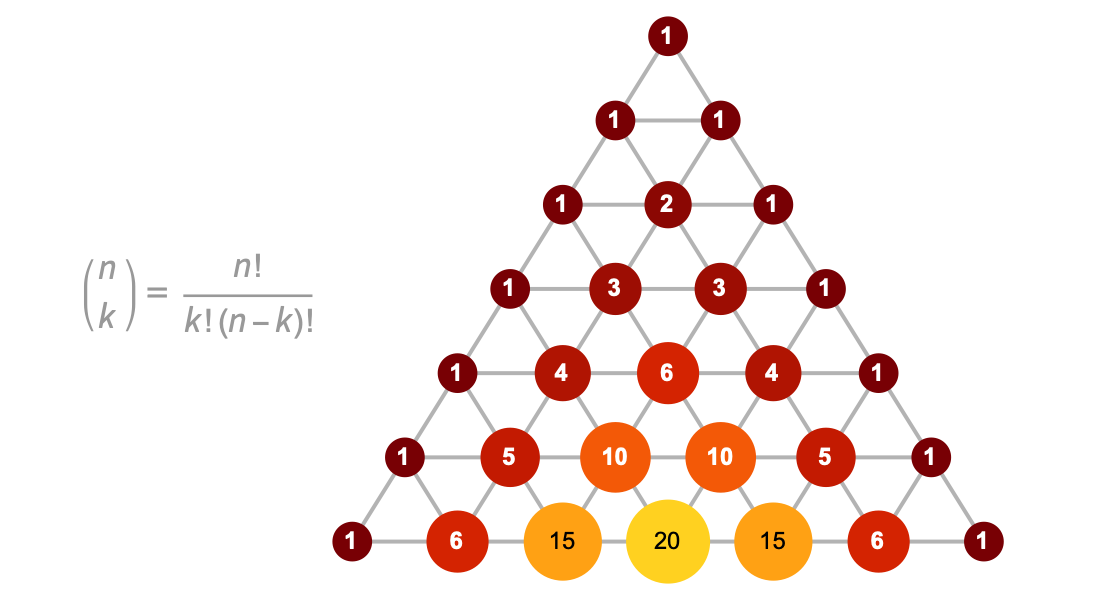
Funciones enteras

Explore secuencias y series con coeficientes binomiales, números de Fibonacci, números armónicos y otras funciones enteras. Utilice la suma simbólica incorporada, la resolución de ecuaciones de recurrencia y el reconocimiento de secuencias para resolver problemas en combinatoria, la teoría de algoritmos y otros dominios.

Propiedades de funciones

Calcule con rapidez más de 15 propiedades matemáticas clave de funciones y sus sumas, productos y composiciones para garantizar la validez matemática de muchos procedimientos.

Computación simbólica

Obtenga soluciones en forma cerrada de primera clase para integrales, ecuaciones diferenciales y docenas de otros problemas. Simplifique fórmulas y calcule respuestas exactas. Ingrese problemas en solucionadores simbólicos de manera precisa y concisa, utilizando el conjunto completo de funciones matemáticas.

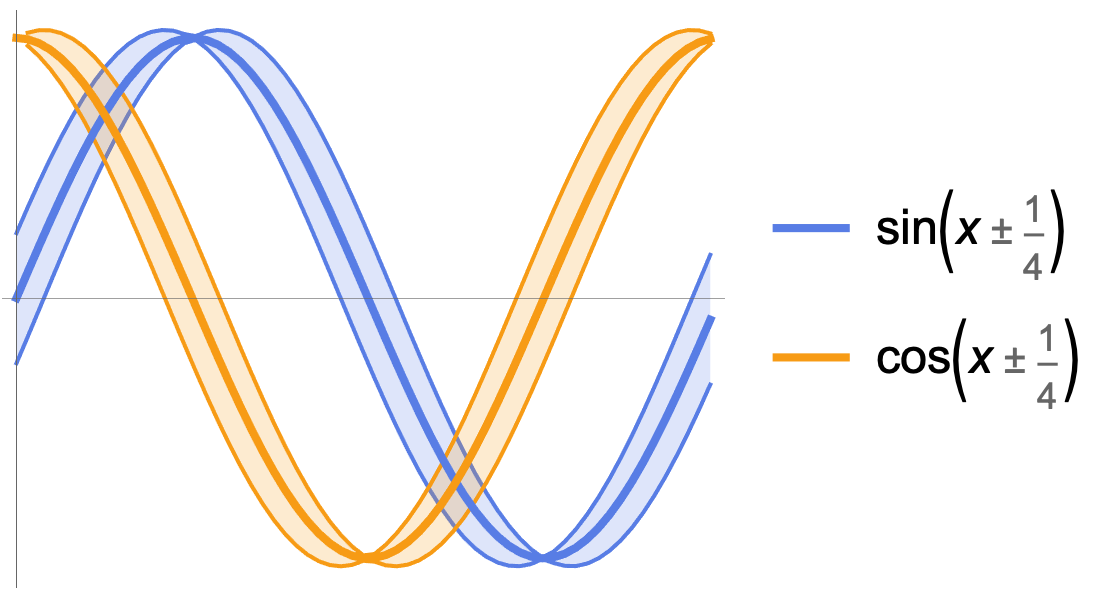
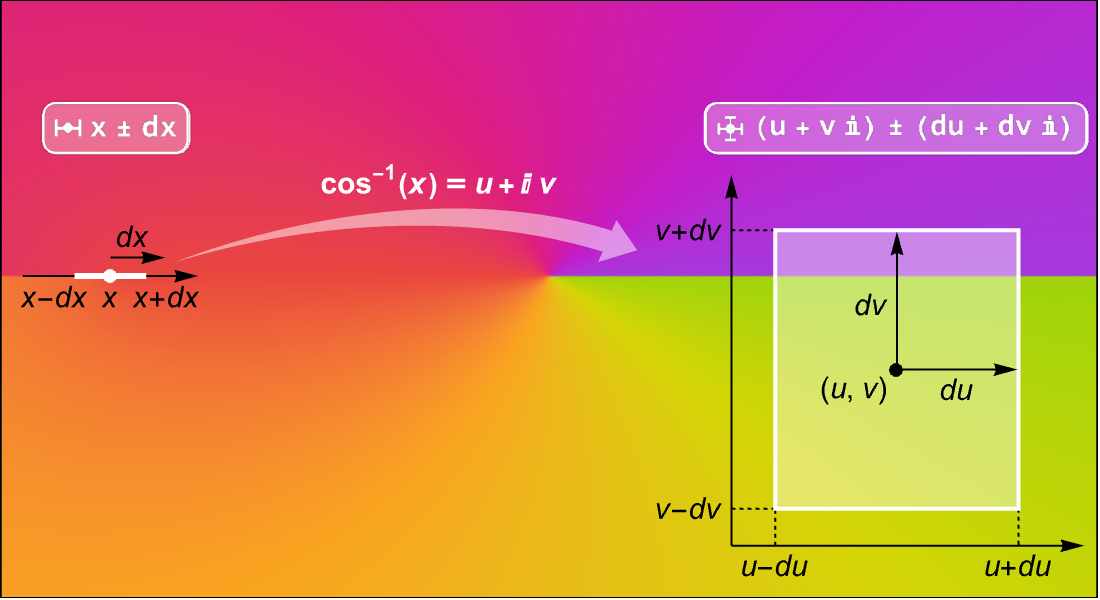
Computación numérica

Calcule el valor de cualquier función matemática con precisión de máquina o a una precisión arbitraria especificada. Realice cálculos con límites rigurosos utilizando intervalos, tanto en la recta real como en el plano complejo. Propague fácilmente las incertidumbres estadísticas. Ingrese problemas en solucionadores numéricos con precisión utilizando cualquier función deseada.

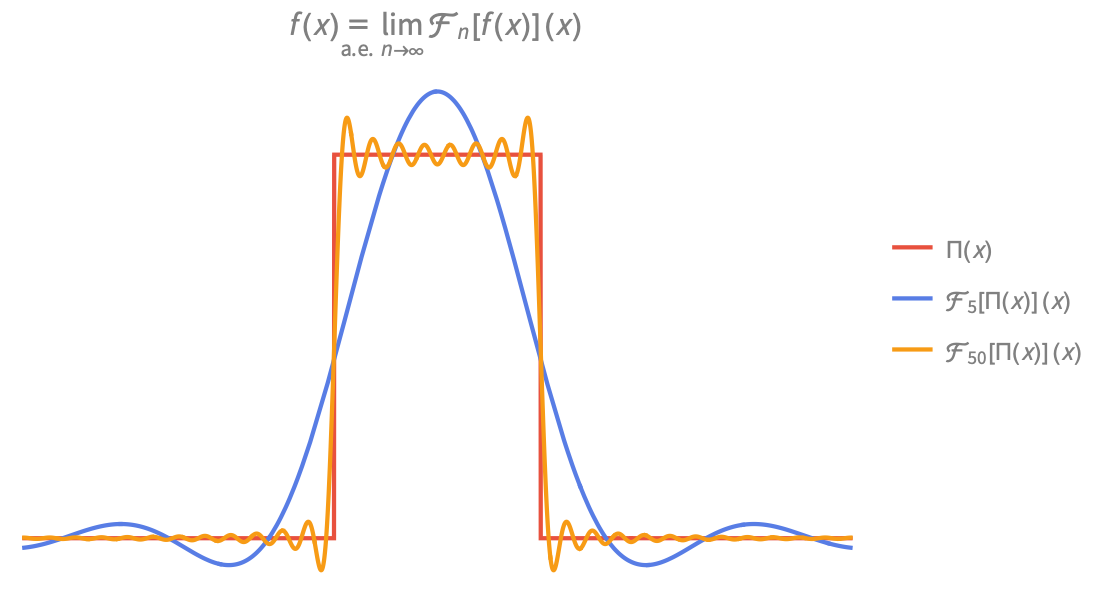
Computación asintótica

Calcule aproximaciones asintóticas de funciones para análisis simbólico de problemas cuando la evaluación simbólica exacta falla y la evaluación numérica no es confiable. Un sistema robusto para series permite que cualquier función analítica se utilice como entrada, y las series generalizadas pueden expresar resultados de manera compacta al continuar utilizando las funciones matemáticas necesarias. 

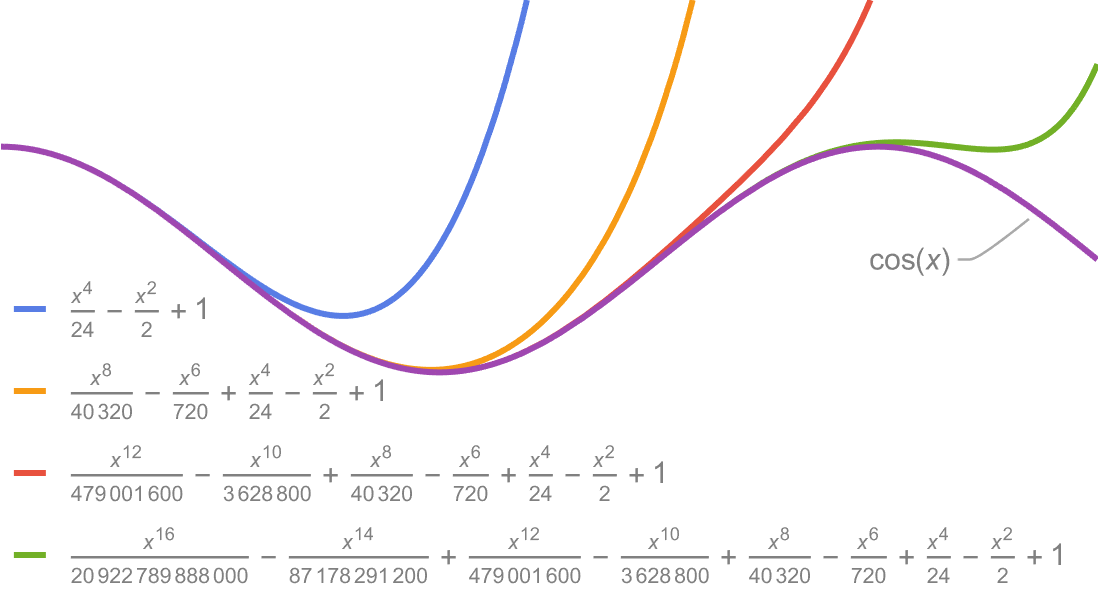
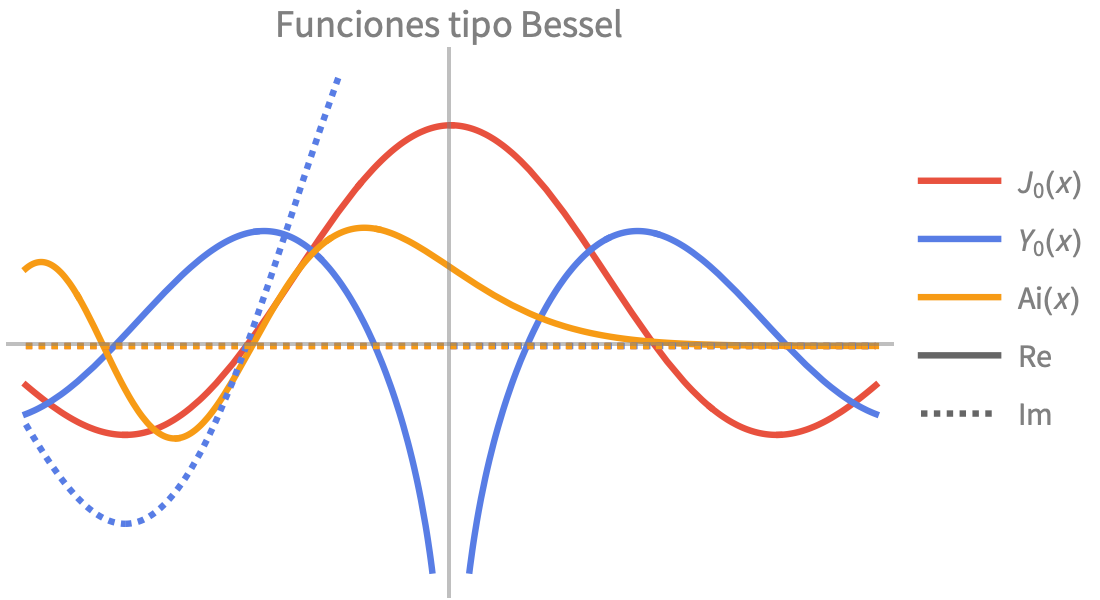
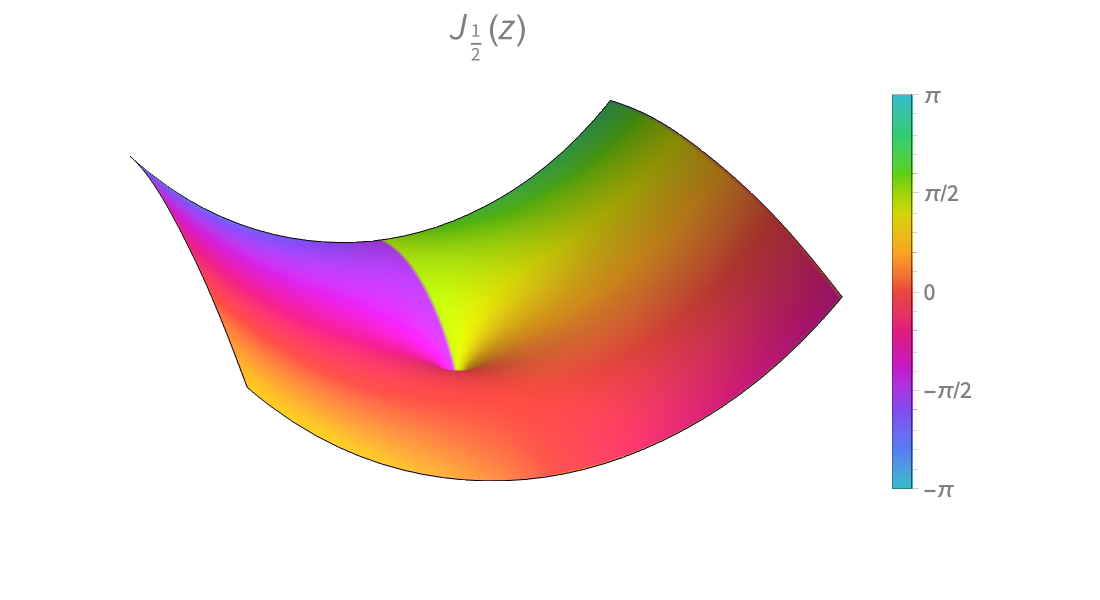
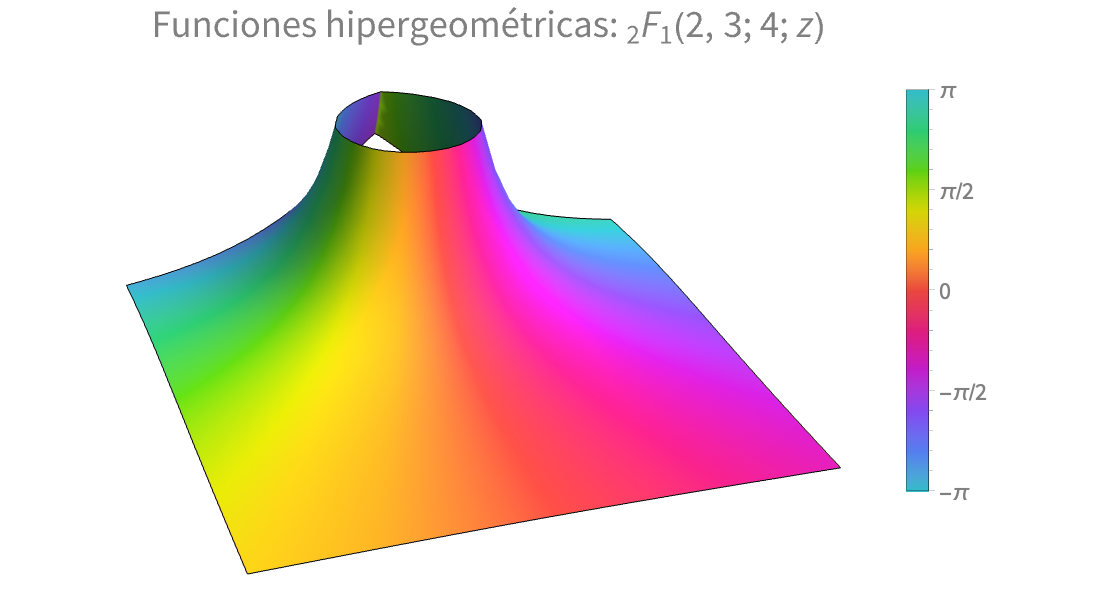
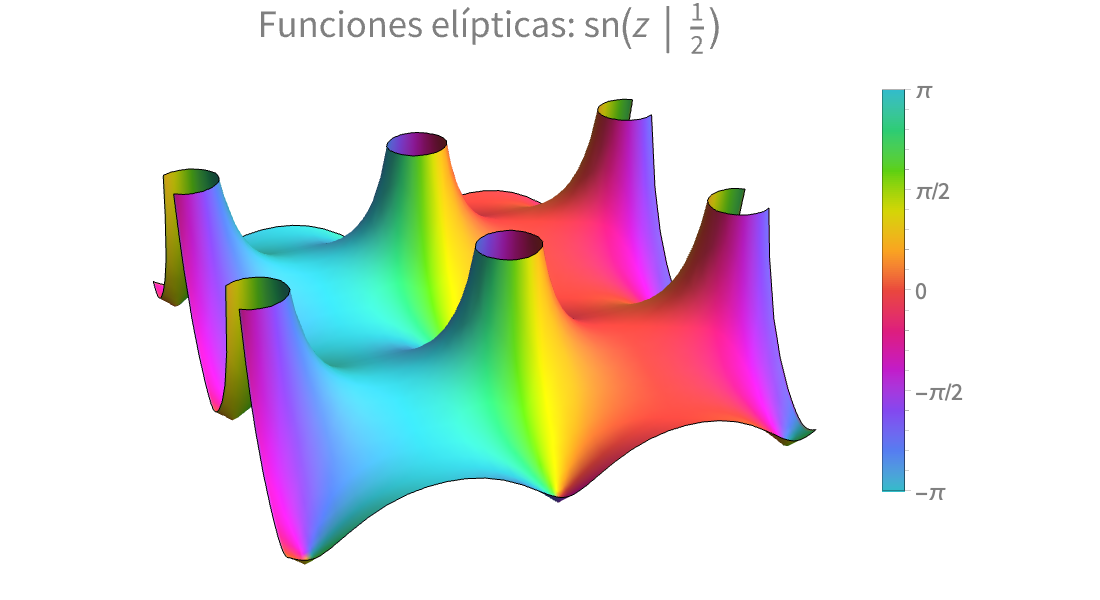
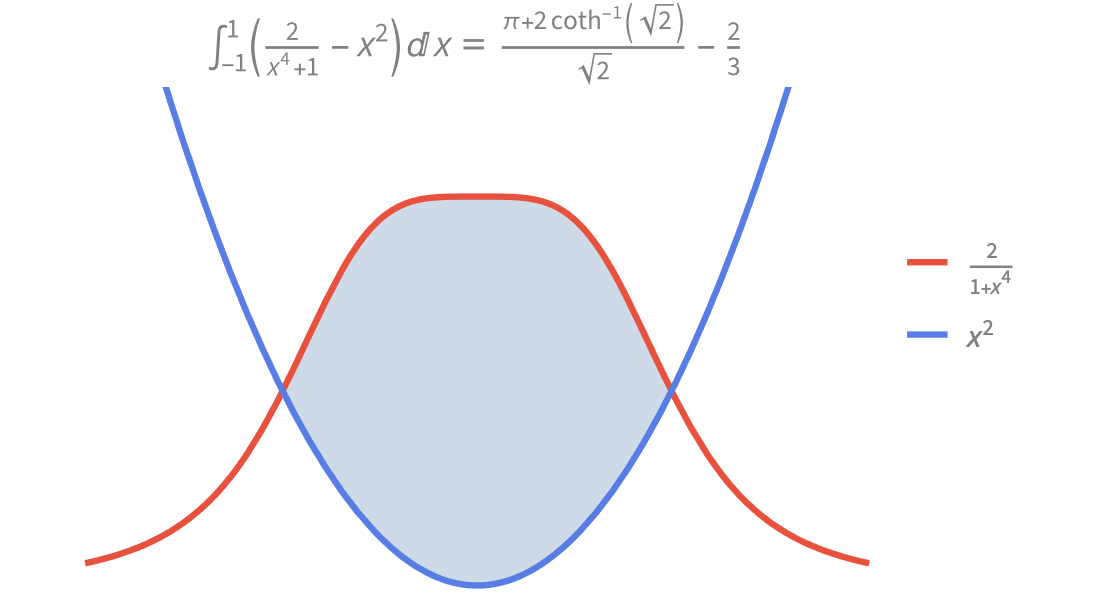
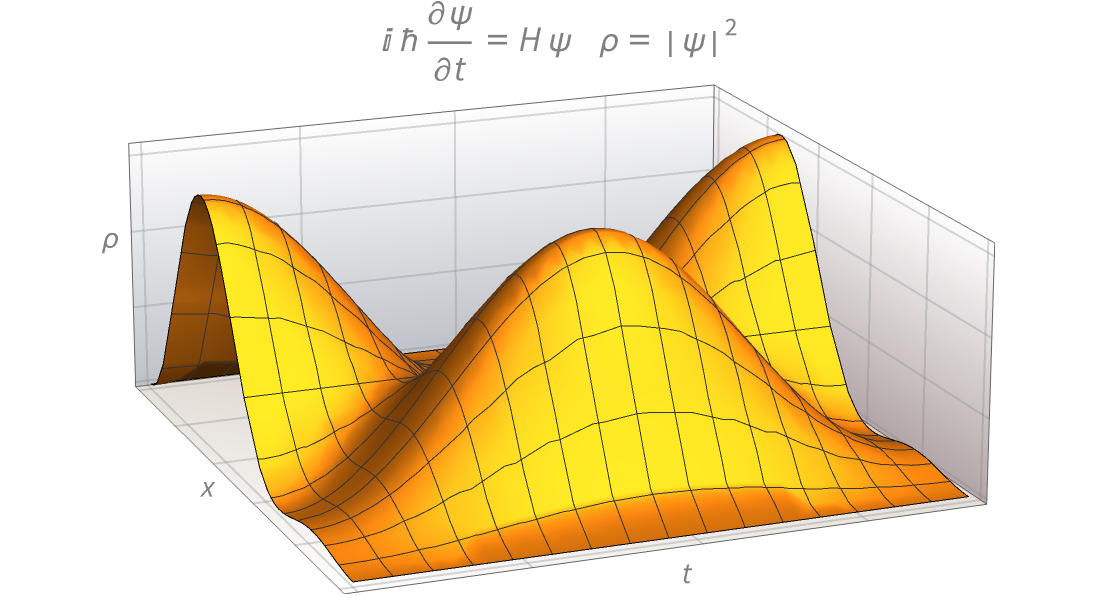
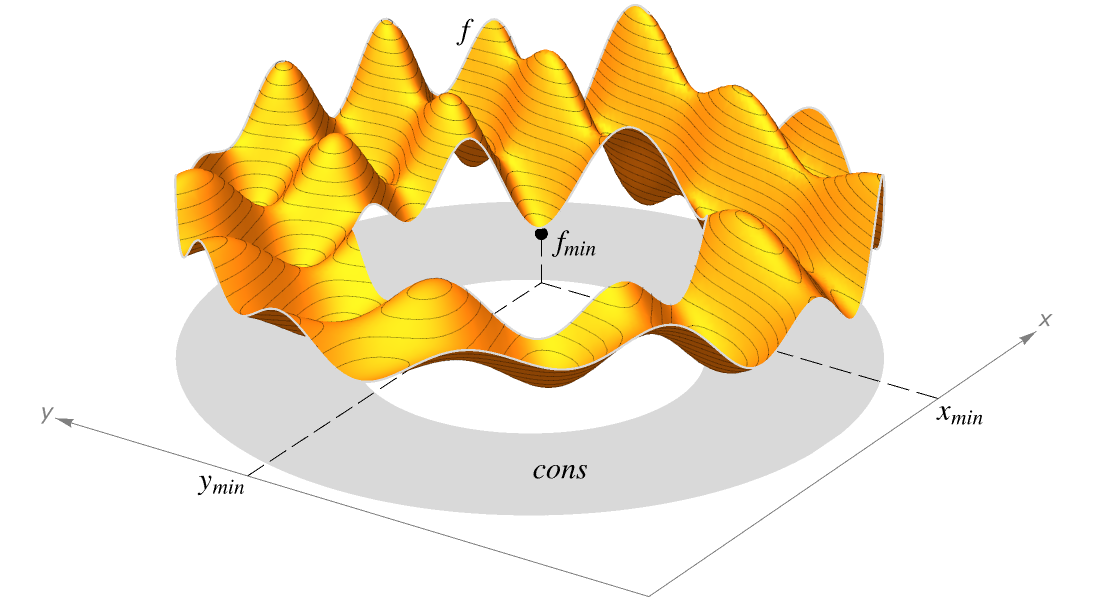
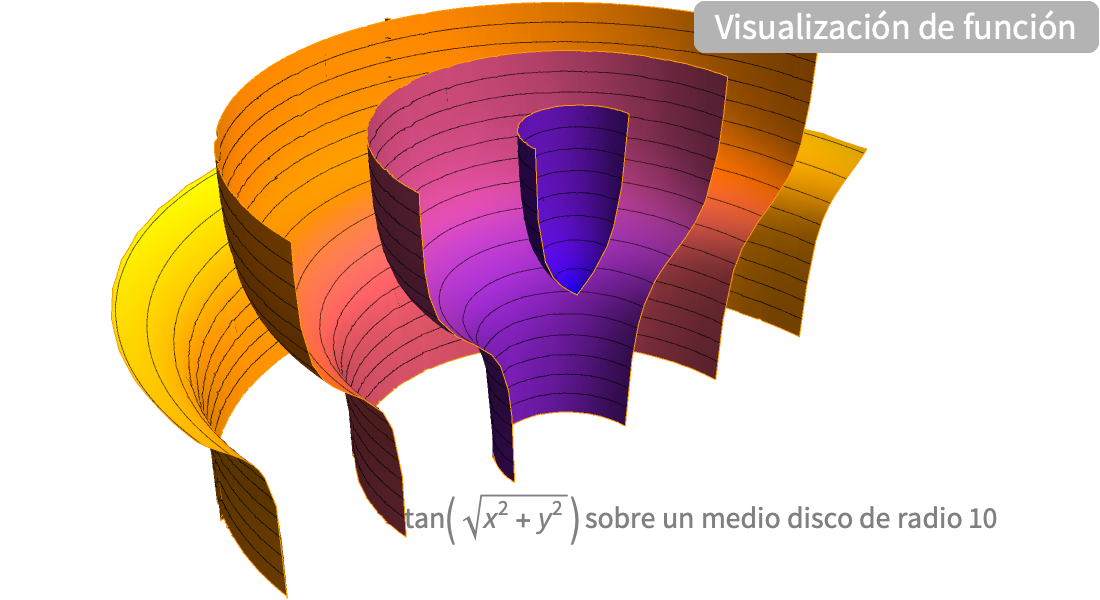
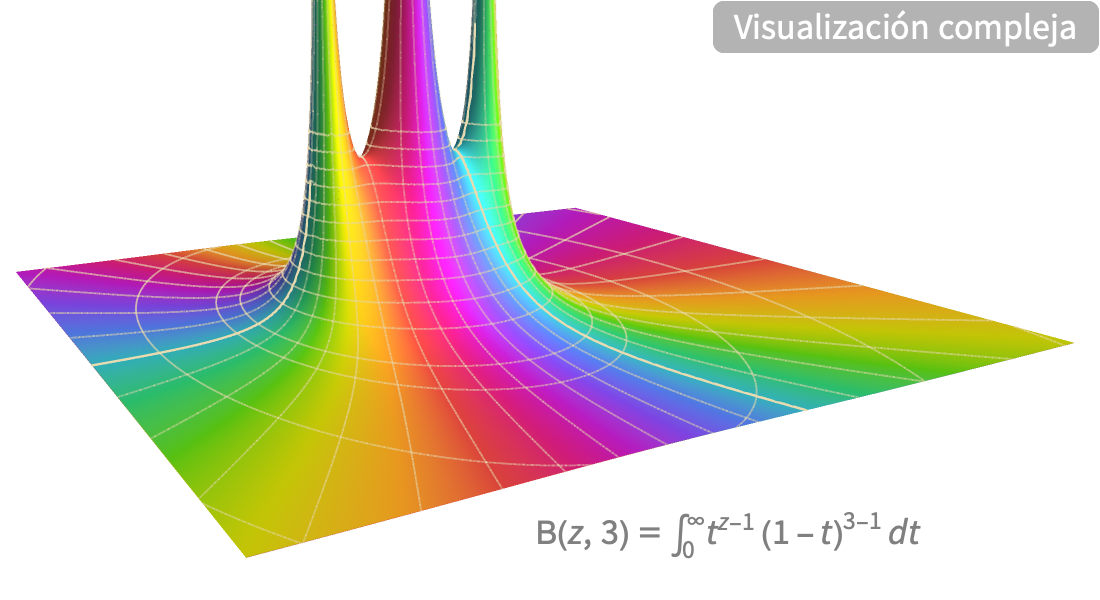
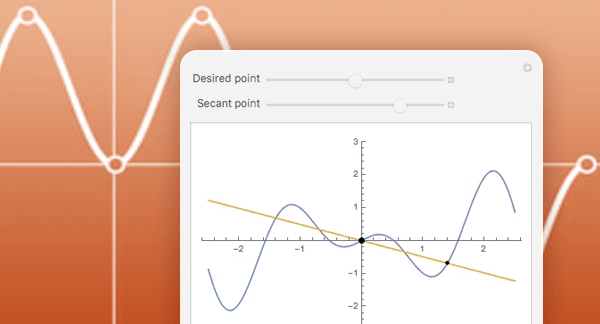
Visualización

Produzca ilustraciones de alta calidad para informes y documentos, y obtenga perspectiva sobre el comportamiento de las funciones matemáticas.

Documentación de Wolfram Funciones matemáticas

Wolfram Funciones matemáticas es una parte integrada de Wolfram Language. El sistema completo contiene más de 6000 funciones incorporadas que abarcan todas las áreas de la computación, todas cuidadosamente integradas de manera que trabajen perfectamente en conjunto.

Alcance completo y documentación de
Wolfram Language

Guide

Guía para funciones elementales

Guide

Guía para funciones especiales

Guide

Guía para funciones matemáticas

Pi ▪ E ▪ EulerGamma ▪ I ▪ Re ▪ Im ▪ Conjugate ▪ Arg ▪ Plus ▪ Times ▪ Total ▪ Abs ▪ Round ▪ Floor ▪ Clip ▪ Ramp ▪ Rescale ▪ DiracDelta ▪ HeavisideTheta ▪ DiracComb ▪ Mod ▪ Quotient ▪ Divisible ▪ GCD ▪ Factorial ▪ Binomial ▪ Fibonacci ▪ BernoulliB ▪ StirlingS1 ▪ IntegerDigits ▪ DigitCount ▪ BitAnd ▪ FactorInteger ▪ Prime ▪ PrimePi ▪ EulerPhi ▪ MoebiusMu ▪ DivisorSigma ▪ JacobiSymbol ▪ MultiplicativeOrder ▪ PartitionsP ▪ SquaresR ▪ DirichletL ▪ FunctionInjective ▪ FunctionSign ▪ FunctionSingularities ▪ NormalDistribution ▪ ChiSquareDistribution ▪ PoissonDistribution ▪ RandomInteger ▪ RandomReal ▪ RandomChoice ▪ RandomPrime ▪ SquareWave ▪ TriangleWave ▪ UnitBox ▪ MandelbrotSetMemberQ ▪ JuliaSetIterationCount ▪ CantorStaircase ▪ MathematicalFunctionData ▪ Gamma ▪ Pochhammer ▪ Beta ▪ PolyGamma ▪ LogGamma ▪ Erf ▪ Erfc ▪ ExpIntegralE ▪ ExpIntegralEi ▪ LogIntegral ▪ FresnelS ▪ SinIntegral ▪ HermiteH ▪ LaguerreL ▪ JacobiP ▪ GegenbauerC ▪ ChebyshevT ▪ ChebyshevU ▪ ZernikeR ▪ SphericalHarmonicY ▪ WignerD ▪ BesselJ ▪ BesselY ▪ BesselI ▪ BesselK ▪ AiryAi ▪ AiryAiPrime ▪ SphericalBesselJ ▪ KelvinBer ▪ HankelH1 ▪ StruveH ▪ LegendreP ▪ LegendreQ ▪ SpheroidalQS ▪ Hypergeometric2F1 ▪ HypergeometricPFQ ▪ HypergeometricU ▪ MeijerG ▪ FoxH ▪ AppellF1 ▪ BilateralHypergeometricPFQ ▪ EllipticK ▪ EllipticF ▪ EllipticE ▪ EllipticPi ▪ CarlsonRF ▪ CarlsonRK ▪ JacobiSN ▪ InverseJacobiSN ▪ WeierstrassP ▪ EllipticTheta ▪ DedekindEta ▪ KleinInvariantJ ▪ ModularLambda ▪ SiegelTheta ▪ Zeta ▪ PolyLog ▪ LerchPhi ▪ RiemannSiegelZ ▪ MathieuS ▪ MathieuSPrime ▪ MathieuC ▪ MathieuCharacteristicA ▪ SpheroidalPS ▪ SpheroidalS1 ▪ SpheroidalEigenvalue ▪ HeunG ▪ HeunC ▪ HeunB ▪ HeunD ▪ HeunT ▪ CoulombF ▪ CoulombG ▪ CoulombH1 ▪ CoulombH2 ▪ QFactorial ▪ QPochhammer ▪ QHypergeometricPFQ ▪ MittagLefflerE ▪ ProductLog ▪ InverseErf ▪ InverseGammaRegularized ▪ InverseEllipticNomeQ ▪ InverseWeierstrassP ▪ BesselJZero ▪ ZetaZero ▪ Root ▪ DifferentialRoot ▪ DifferenceRoot ▪ Derivative ▪ FindRoot ▪ Min ▪ Max ▪ RealAbs ▪ Piecewise ▪ Log ▪ Log10 ▪ Log2 ▪ Exp ▪ Power ▪ Sqrt ▪ CubeRoot ▪ Surd ▪ Degree ▪ Sin ▪ Cos ▪ Tan ▪ ArcSin ▪ ArcCos ▪ ArcTan ▪ Sinc ▪ Sinh ▪ Cosh ▪ Tanh ▪ ArcSinh ▪ ArcCosh ▪ ArcTanh ▪ N ▪ FunctionExpand ▪ FullSimplify ▪ Series ▪