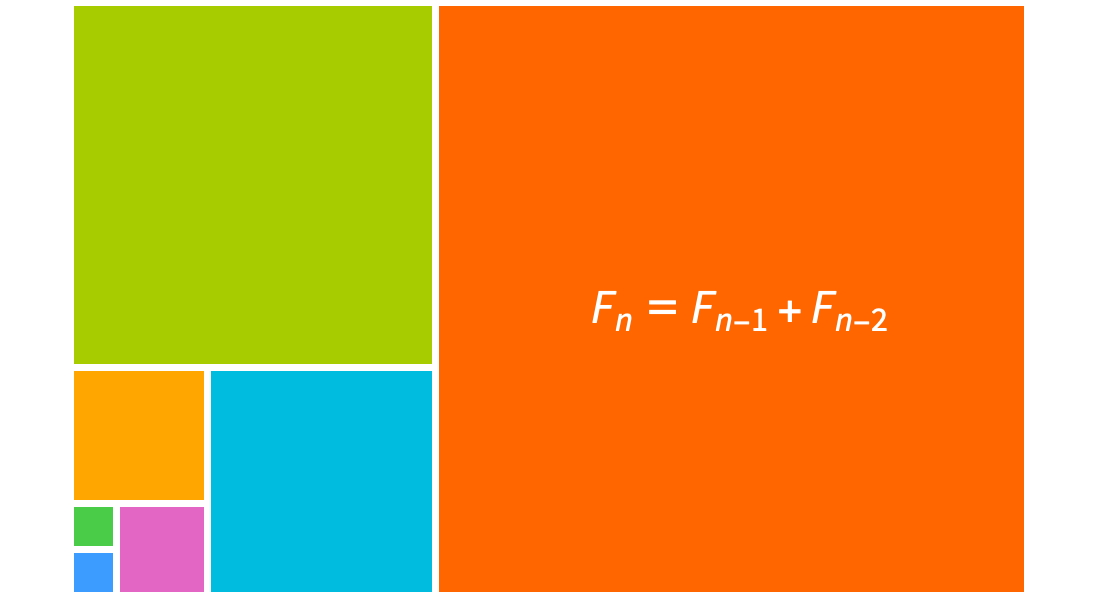WolframFonctions mathématiquesUn élément essentiel de
Wolfram Language

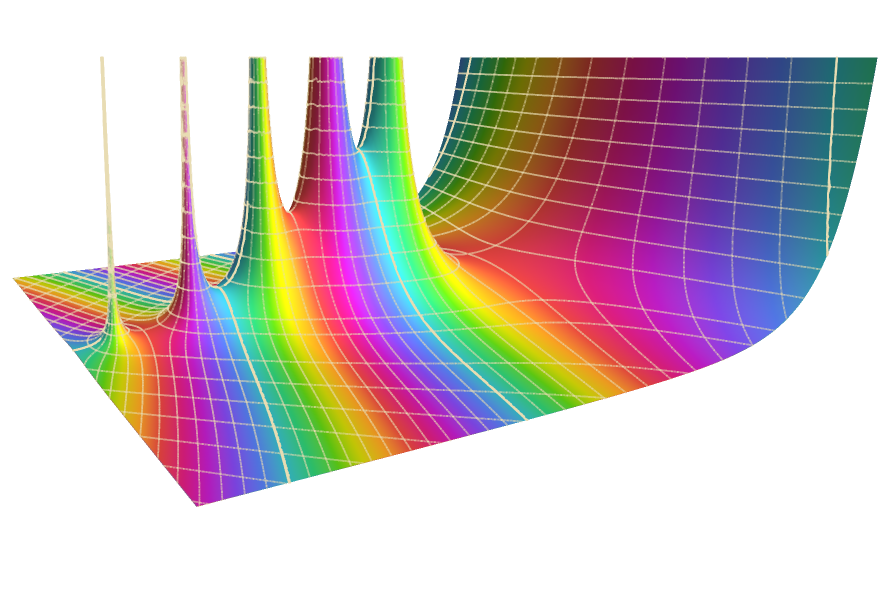
Définissez, calculez et visualisez.

Évaluation symbolique et numérique, visualisation et développements asymptotiques d'une vaste collection de fonctions mathématiques, largement documentées et étroitement intégrées à tous les domaines de Wolfram Language.

Démarrer

La collection la plus complète

Avec des centaines de fonctions de base et de fonctions spéciales avancées, la vaste collection est étroitement intégrée dans les solveurs symboliques et numériques. Calculez des résultats numériques avec la précision souhaitée et trouvez ou simplifiez des formules. Une documentation exhaustive, multi-niveaux et interactive permet à chacun d'exploiter leur puissance.

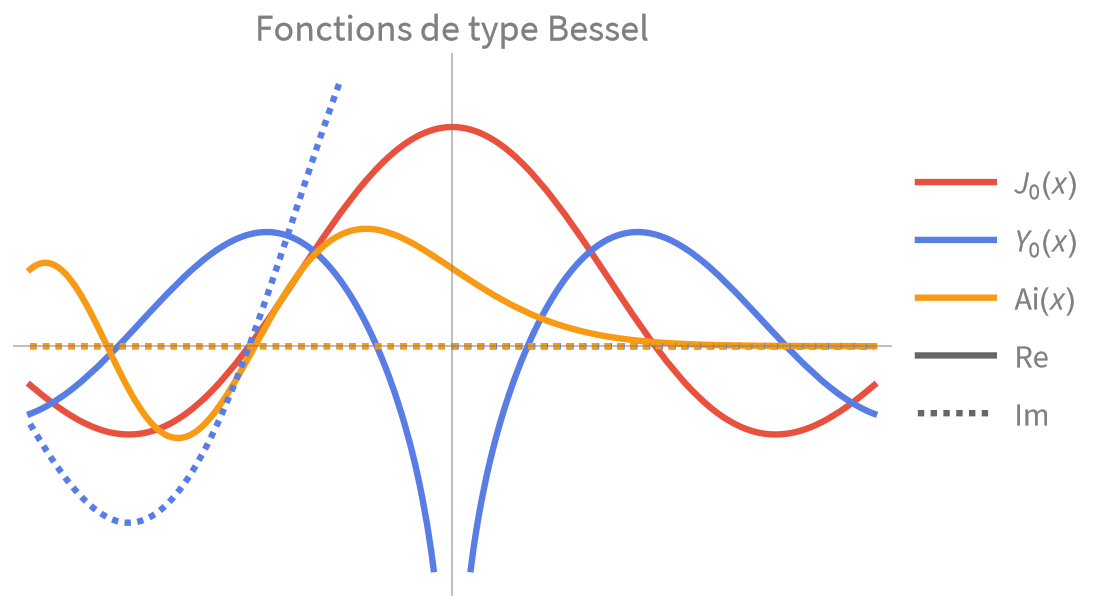
Fonctions de base

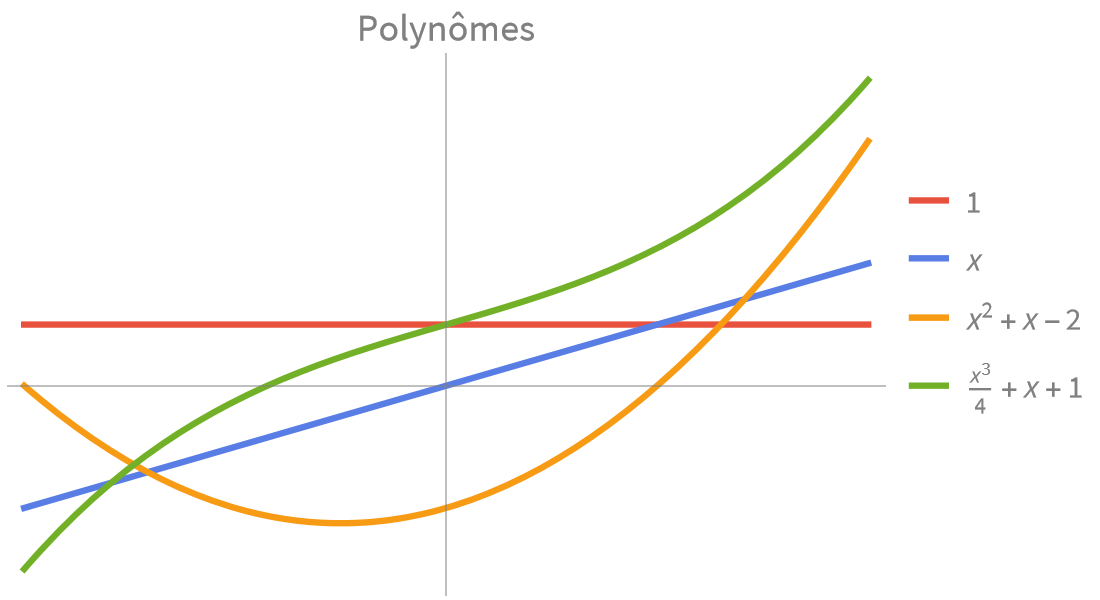
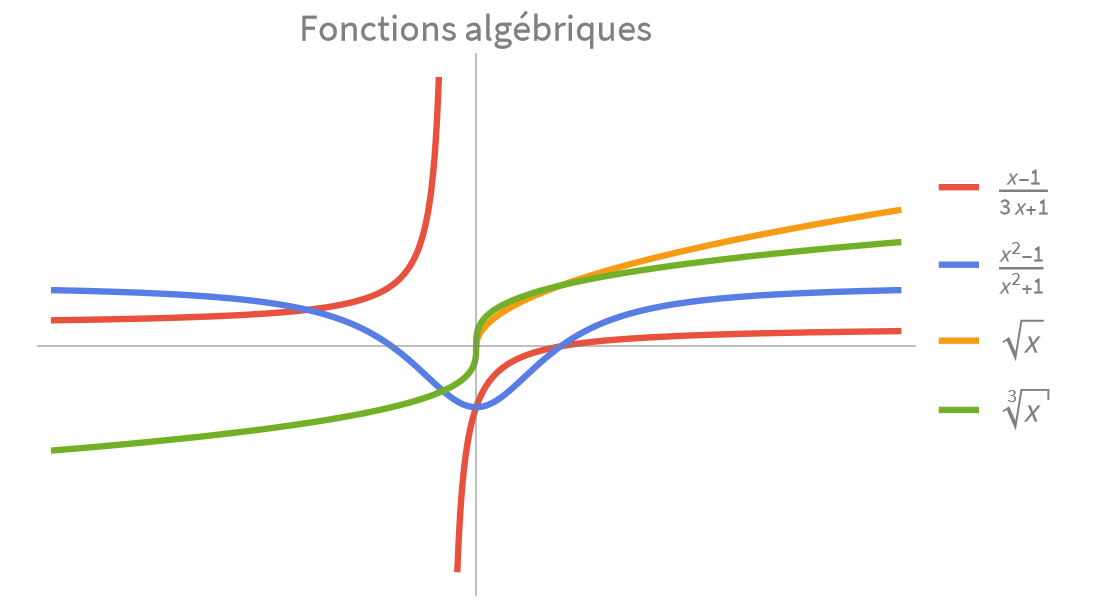
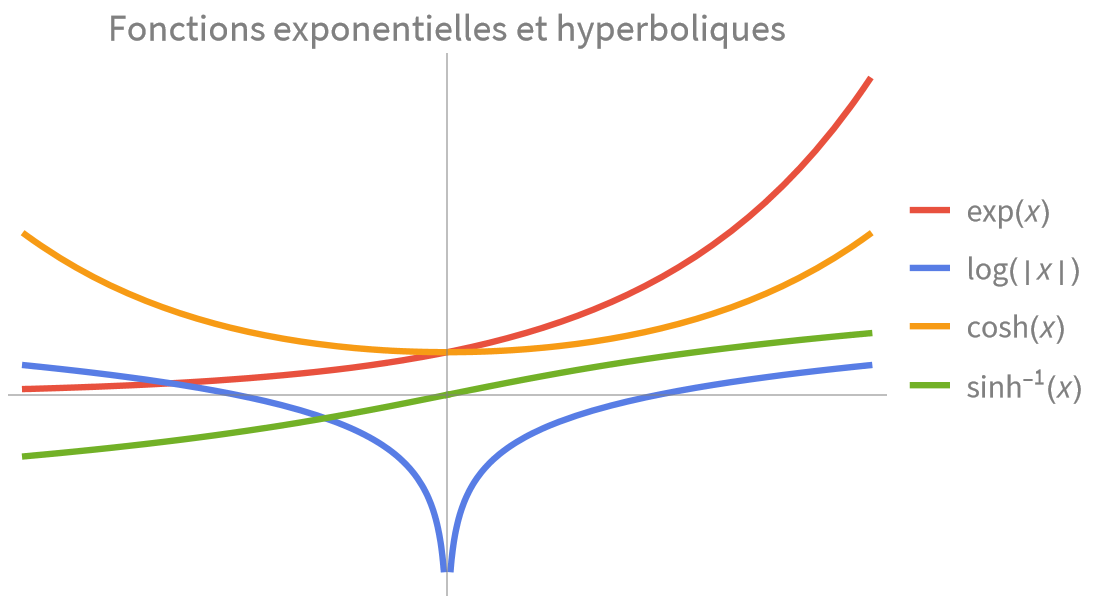
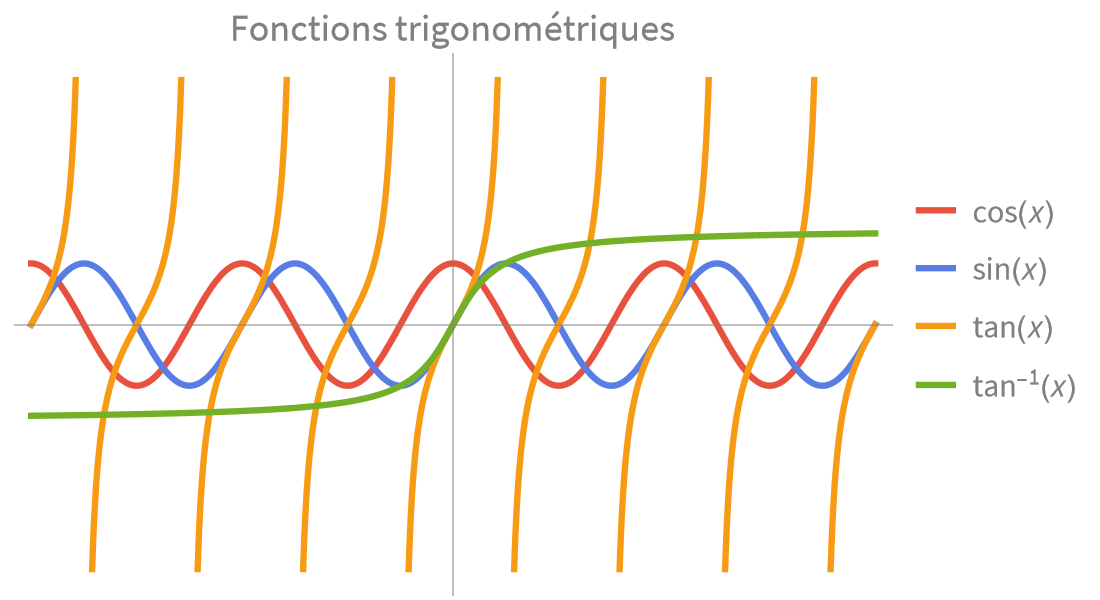
Calcul numérique et symbolique rapide et précis pour les applications scientifiques et techniques. Fonctions exponentielles, trigonométriques et hyperboliques intégrées pour modéliser les combinaisons de croissance, de décroissance et de comportement oscillatoire.

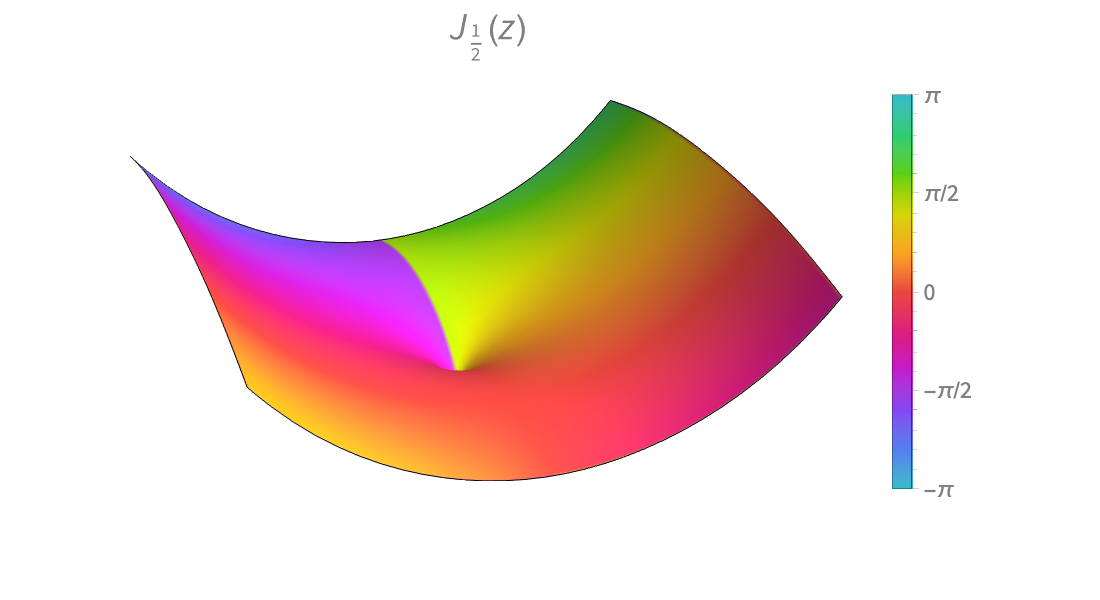
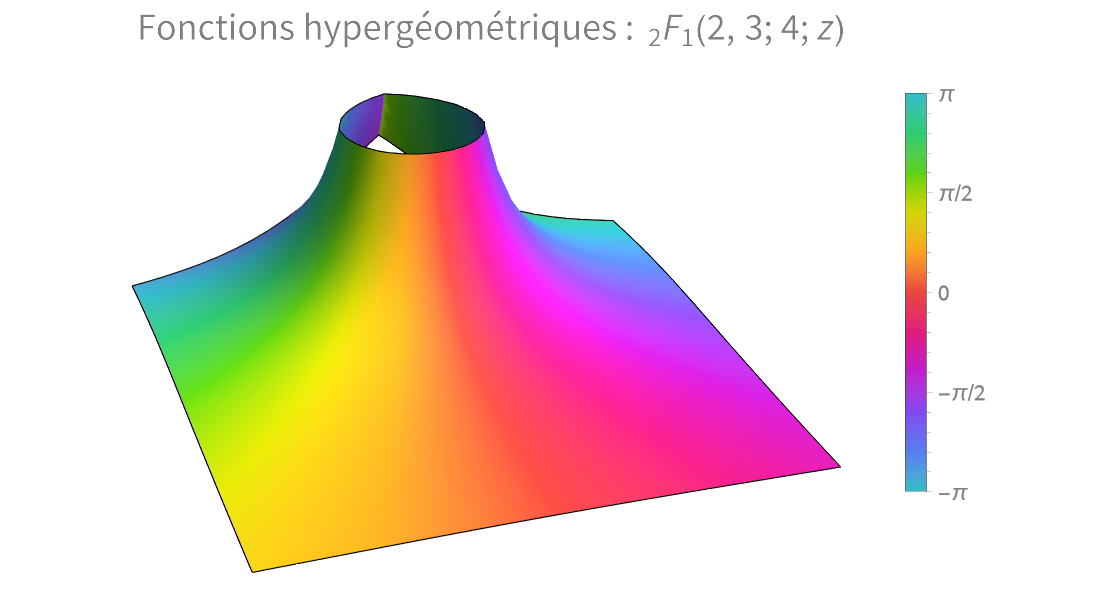
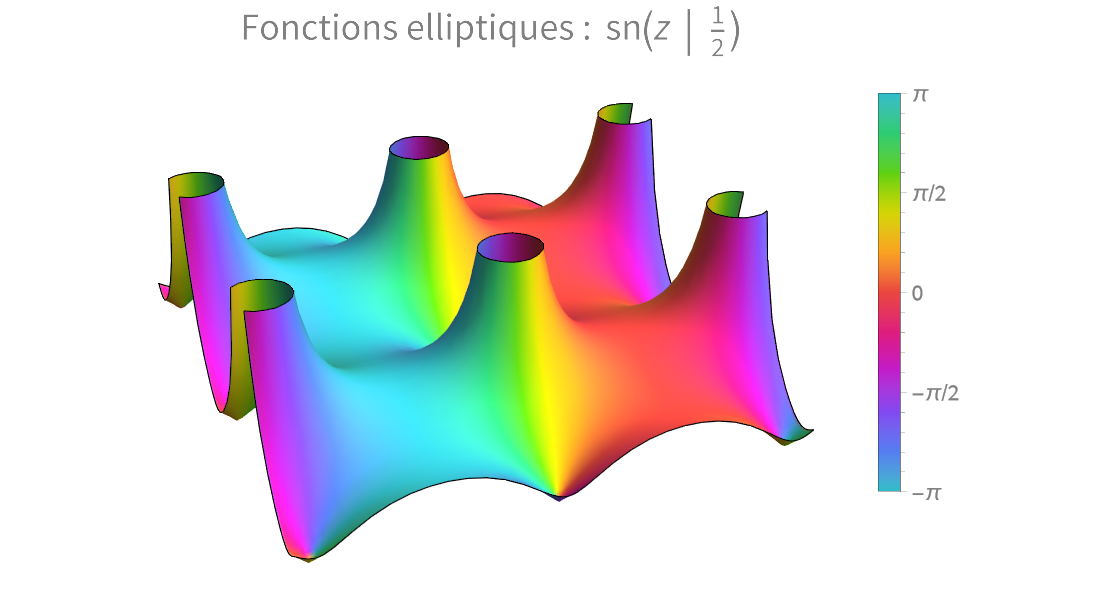
Fonctions spéciales

Résolvez des problèmes de physique, d'ingénierie, de probabilité et de statistiques à l'aide de calculs numériques de haute précision ou de développements symboliques de séries.

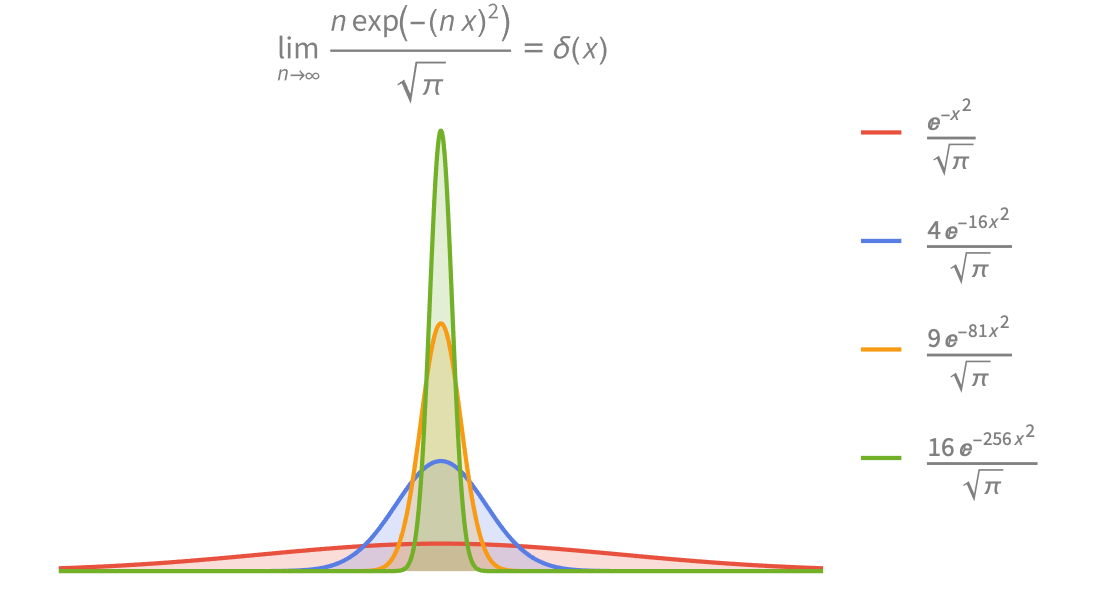
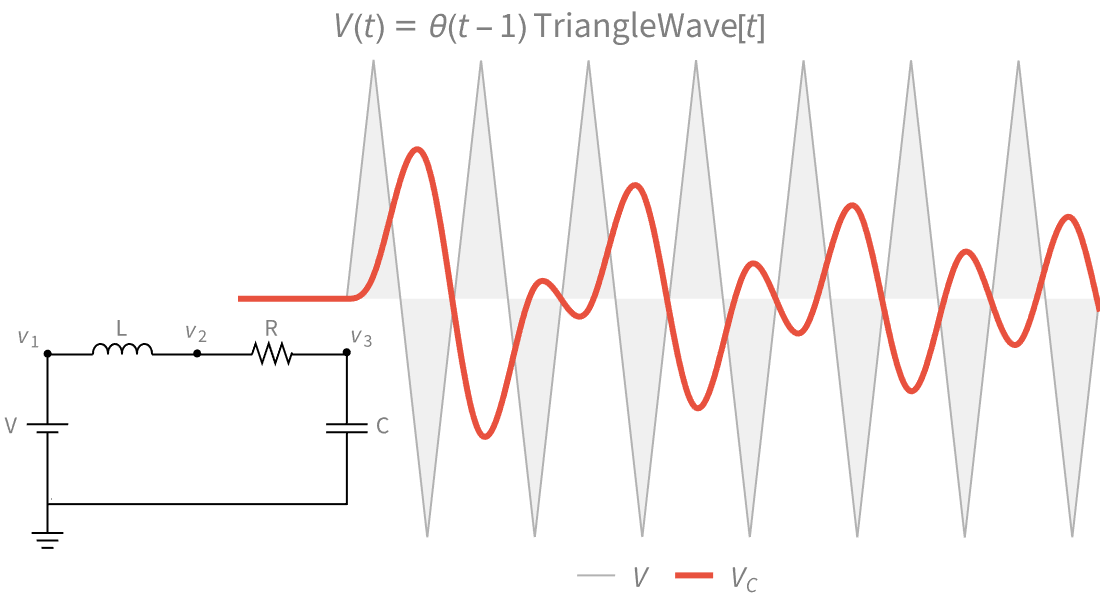
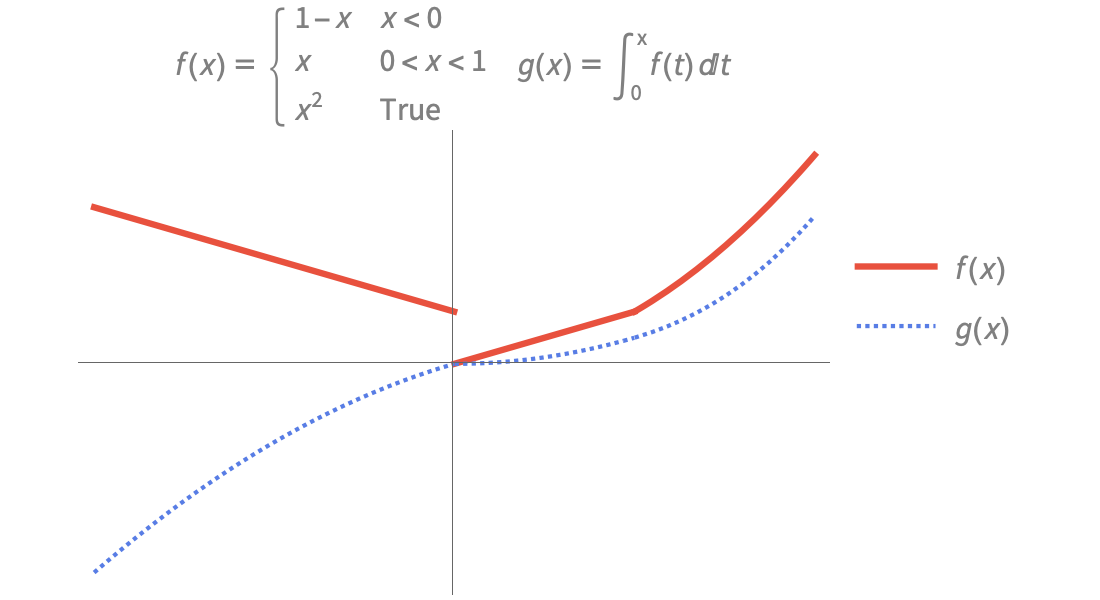
Fonctions par morceaux et fonctions généralisées

Modélisez des systèmes techniques et physiques à l'aide d'une gamme complète de fonctions par morceaux et de fonctions généralisées définies par points. Construisez vos propres fonctions à l'aide de Piecewise.

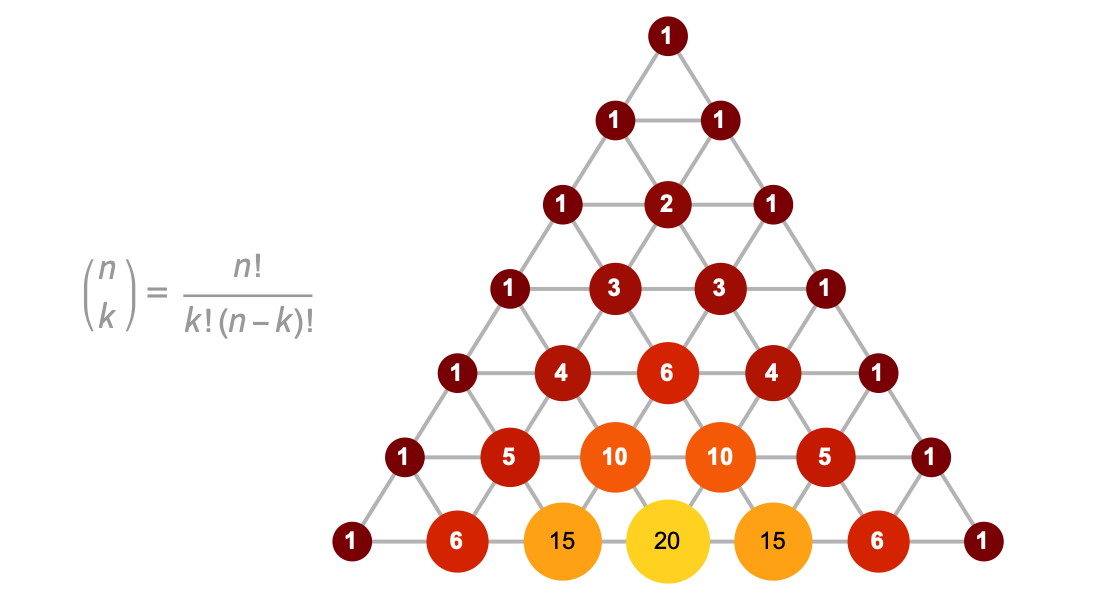
Fonctions sur les nombres entiers

Explorez les séquences et les séries à coefficients binomiaux, les nombres de Fibonacci et les nombres harmoniques, ainsi que d'autres fonctions sur les nombres entiers. Utilisez la sommation symbolique intégrée, la résolution d'équations de récurrence et la reconnaissance de séquences pour résoudre des problèmes en combinatoire, en théorie des algorithmes et dans d'autres domaines.

Propriétés des fonctions

Calculez rapidement plus de 15 propriétés mathématiques clés des fonctions et de leurs sommes, produits et compositions afin de garantir la validité mathématique de nombreuses procédures.

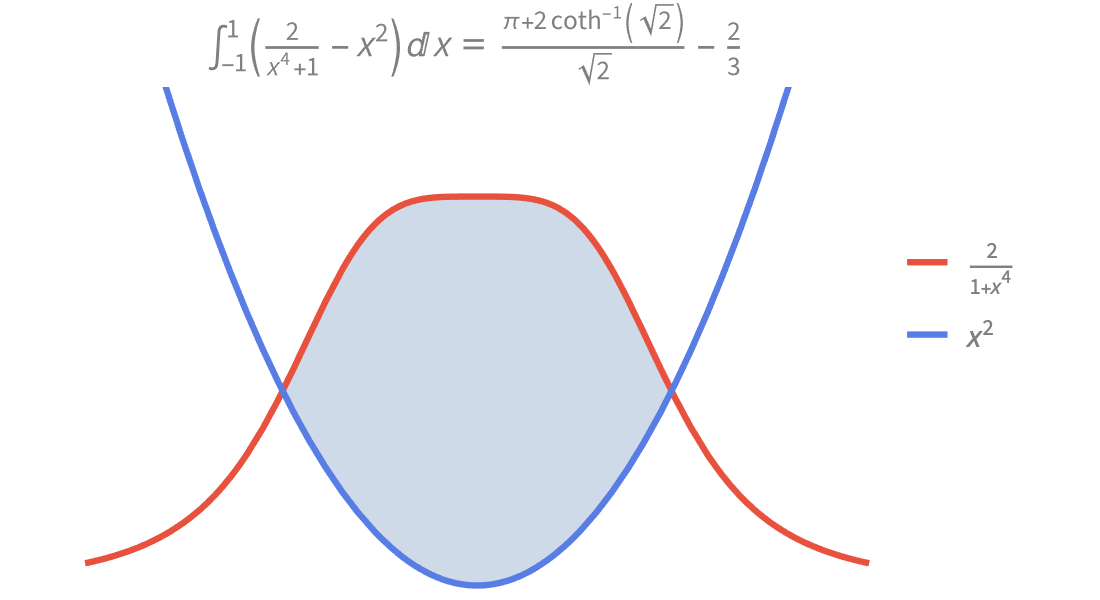
Calcul symbolique

Obtenez les meilleures solutions de forme fermée pour les intégrales, les équations différentielles et des dizaines d'autres problèmes. Simplifiez les formules et calculez des réponses exactes. Entrez les problèmes dans les solveurs symboliques de manière précise et concise, en utilisant l'ensemble complet de fonctions mathématiques.

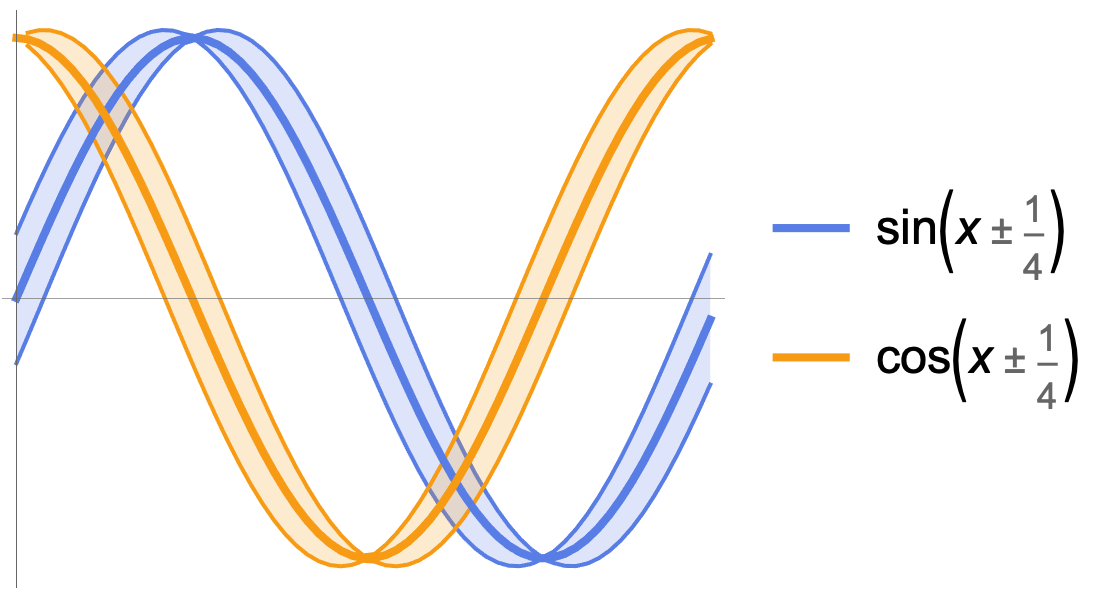
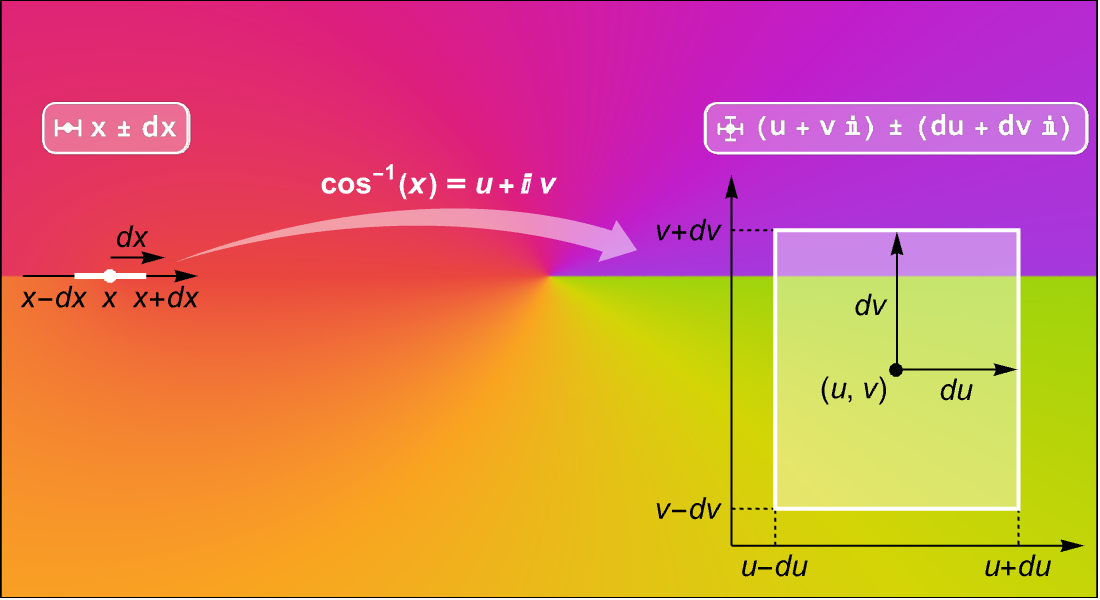
Calcul numérique

Calculez la valeur de n'importe quelle fonction mathématique à virgule flottante ou précision arbitraire spécifiée. Calculez avec des limites rigoureuses en utilisant des intervalles, à la fois sur la droite réelle et dans le plan complexe. Propagez facilement les incertitudes statistiques. Introduisez les problèmes dans les solveurs numériques avec précision et avec n'importe quelle fonction souhaitée.

Calcul asymptotique

Calculez des approximations asymptotiques de fonctions pour l'analyse symbolique de problèmes lorsque l'évaluation symbolique exacte échoue et que l'évaluation numérique n'est pas fiable. Un système robuste pour les séries permet d'utiliser n'importe quelle fonction analytique en entrée, et les séries généralisées peuvent exprimer des résultats de manière compacte en continuant à utiliser les fonctions mathématiques nécessaires.

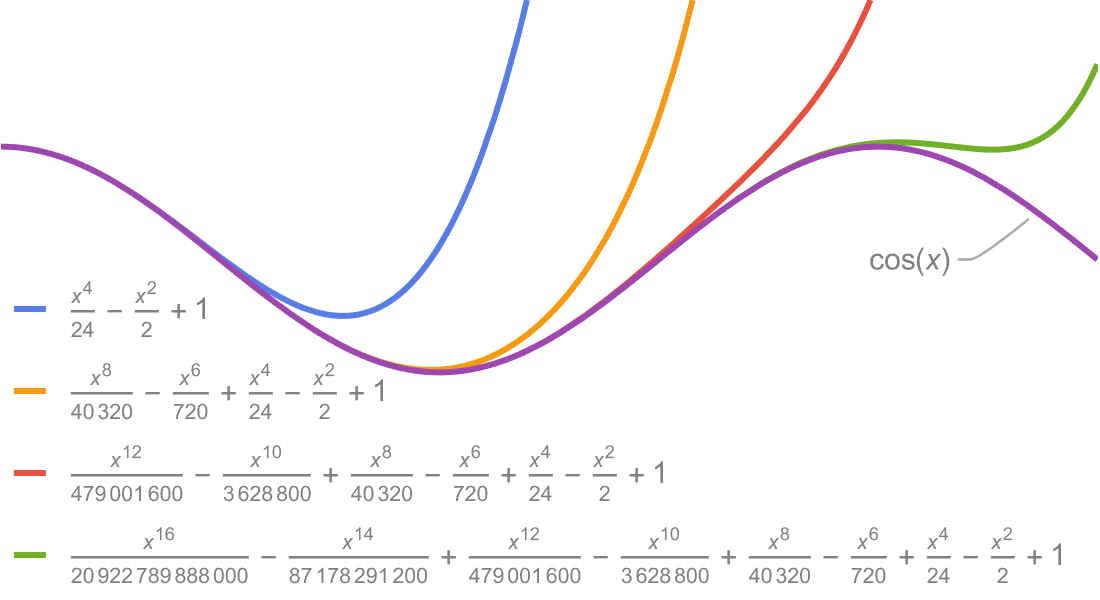
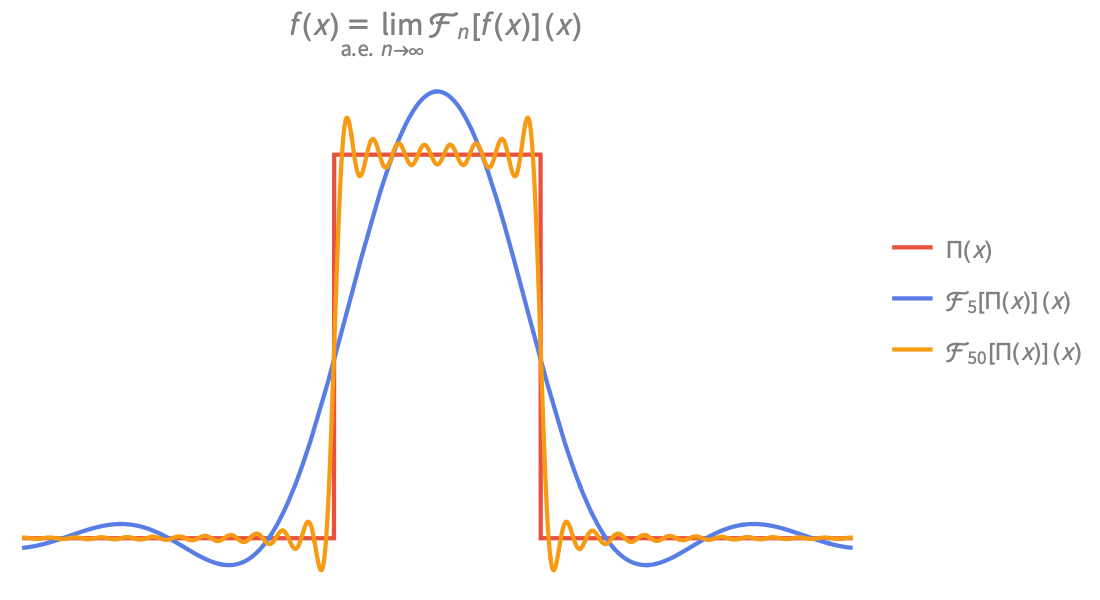
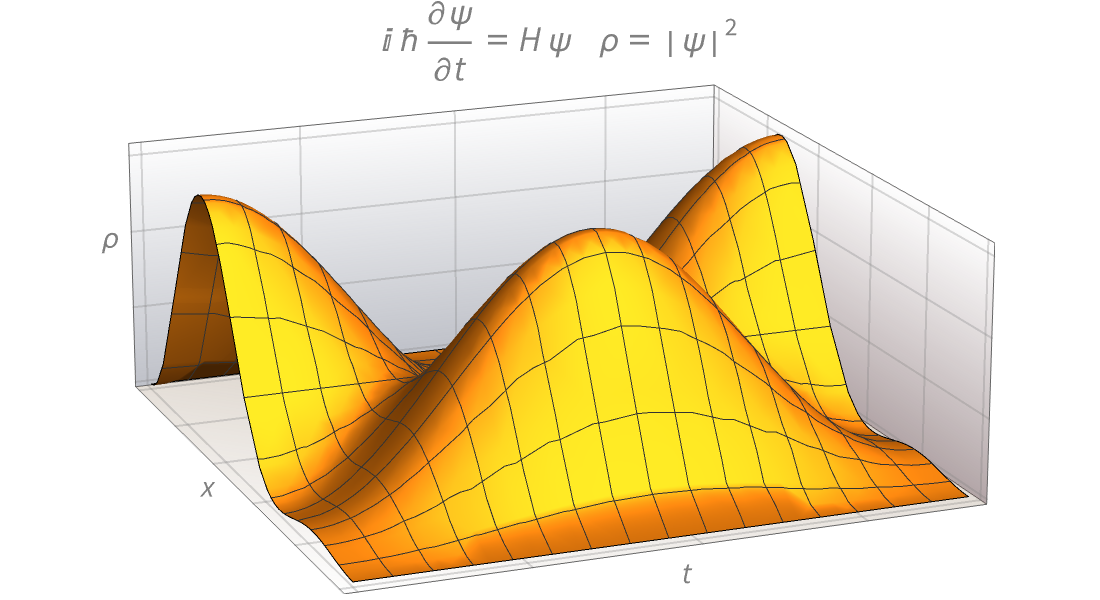
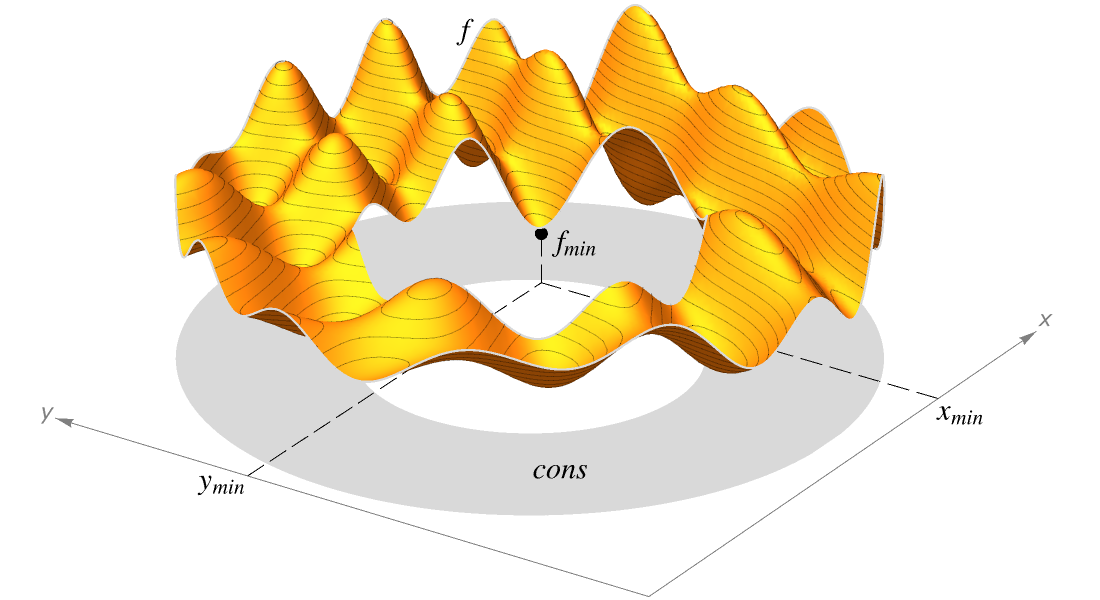
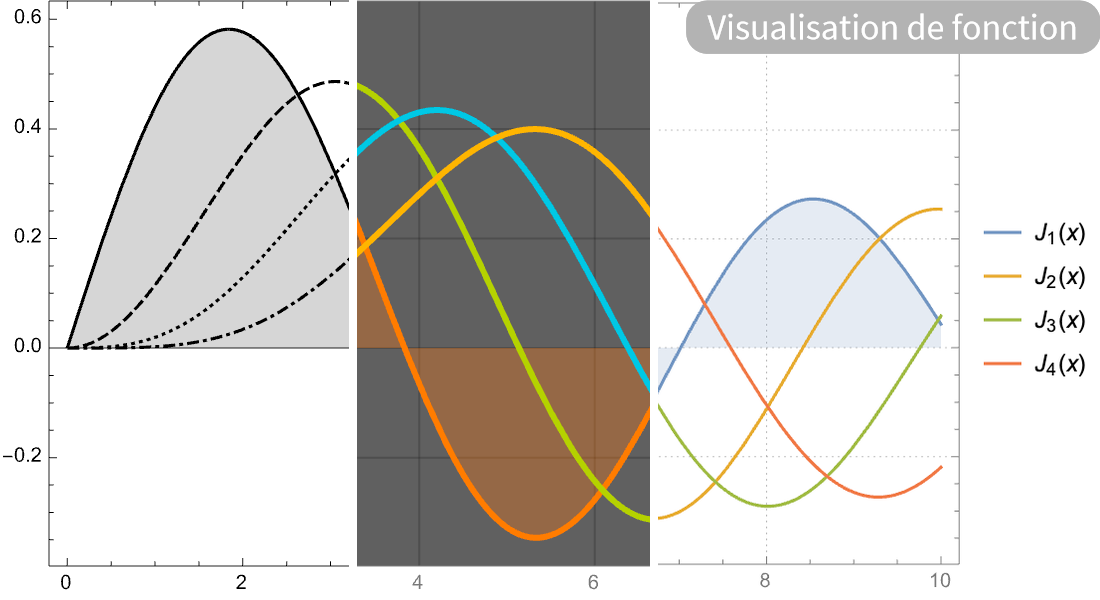
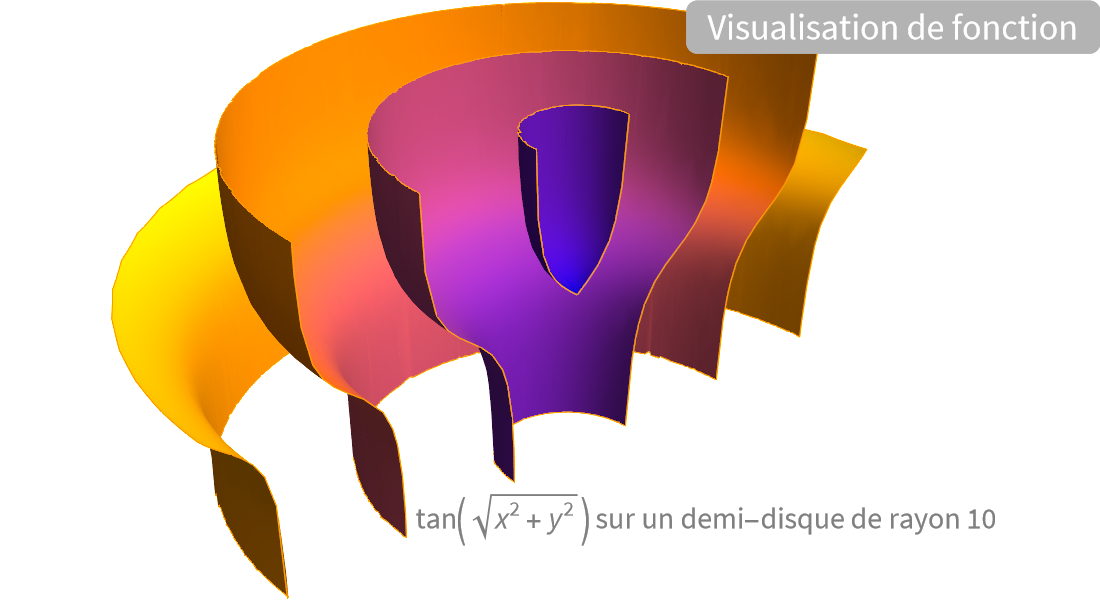
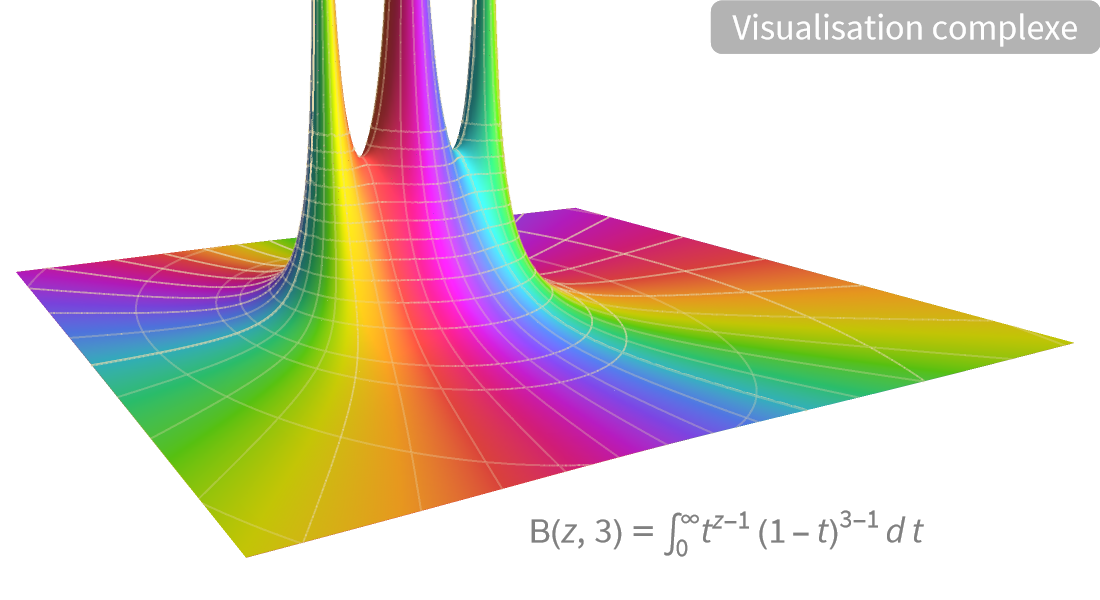
Visualisation

Produisez des illustrations de haute qualité pour des rapports et des articles et obtenez un aperçu du comportement des fonctions mathématiques.

Documentation de Wolfram Fonctions mathématiques

Wolfram Fonctions mathématiques fait partie intégrante de Wolfram Language. Le système complet contient plus de 6000 fonctions intégrées couvrant tous les domaines du calcul, toutes soigneusement intégrées pour fonctionner parfaitement ensemble.

Wolfram Language
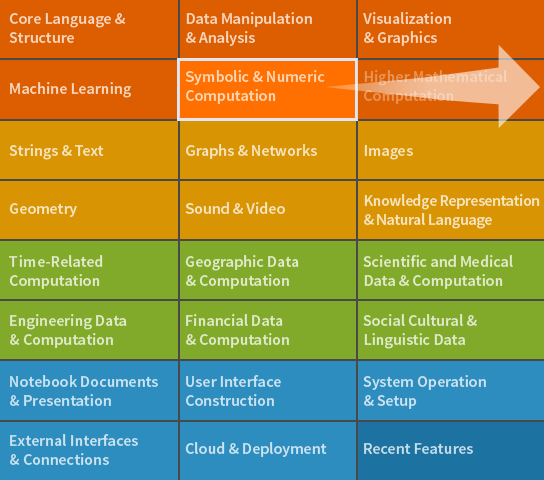
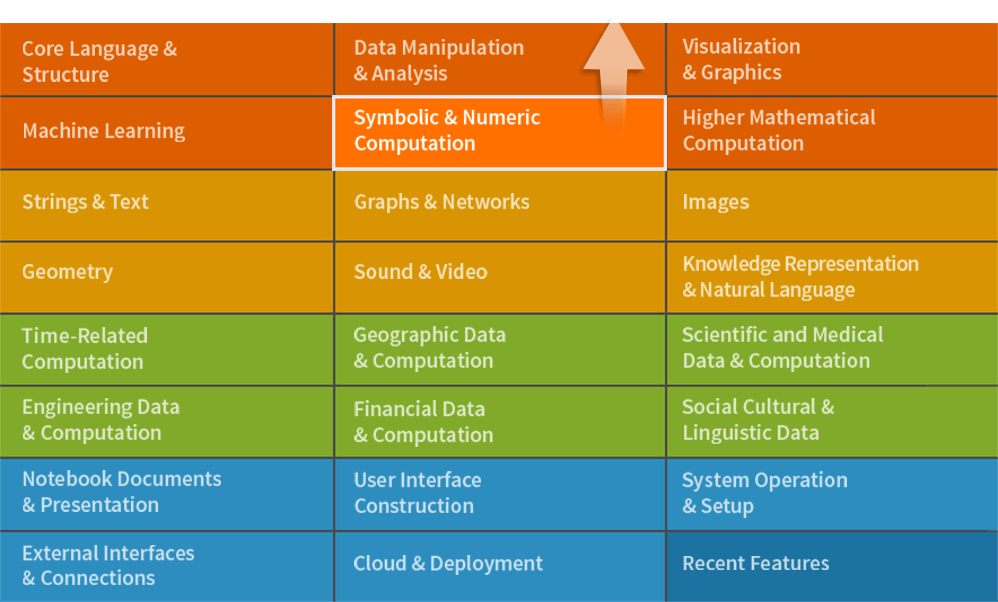
Champ d'application et documentation

Guide

Guide pour les fonctions de base

Guide

Guide pour les fonctions spéciales

Guide

Guide pour les fonctions mathématiques

Pi ▪ E ▪ EulerGamma ▪ I ▪ Re ▪ Im ▪ Conjugate ▪ Arg ▪ Plus ▪ Times ▪ Total ▪ Abs ▪ Round ▪ Floor ▪ Clip ▪ Ramp ▪ Rescale ▪ DiracDelta ▪ HeavisideTheta ▪ DiracComb ▪ Mod ▪ Quotient ▪ Divisible ▪ GCD ▪ Factorial ▪ Binomial ▪ Fibonacci ▪ BernoulliB ▪ StirlingS1 ▪ IntegerDigits ▪ DigitCount ▪ BitAnd ▪ FactorInteger ▪ Prime ▪ PrimePi ▪ EulerPhi ▪ MoebiusMu ▪ DivisorSigma ▪ JacobiSymbol ▪ MultiplicativeOrder ▪ PartitionsP ▪ SquaresR ▪ DirichletL ▪ FunctionInjective ▪ FunctionSign ▪ FunctionSingularities ▪ NormalDistribution ▪ ChiSquareDistribution ▪ PoissonDistribution ▪ RandomInteger ▪ RandomReal ▪ RandomChoice ▪ RandomPrime ▪ SquareWave ▪ TriangleWave ▪ UnitBox ▪ MandelbrotSetMemberQ ▪ JuliaSetIterationCount ▪ CantorStaircase ▪ MathematicalFunctionData ▪ Gamma ▪ Pochhammer ▪ Beta ▪ PolyGamma ▪ LogGamma ▪ Erf ▪ Erfc ▪ ExpIntegralE ▪ ExpIntegralEi ▪ LogIntegral ▪ FresnelS ▪ SinIntegral ▪ HermiteH ▪ LaguerreL ▪ JacobiP ▪ GegenbauerC ▪ ChebyshevT ▪ ChebyshevU ▪ ZernikeR ▪ SphericalHarmonicY ▪ WignerD ▪ BesselJ ▪ BesselY ▪ BesselI ▪ BesselK ▪ AiryAi ▪ AiryAiPrime ▪ SphericalBesselJ ▪ KelvinBer ▪ HankelH1 ▪ StruveH ▪ LegendreP ▪ LegendreQ ▪ SpheroidalQS ▪ Hypergeometric2F1 ▪ HypergeometricPFQ ▪ HypergeometricU ▪ MeijerG ▪ FoxH ▪ AppellF1 ▪ BilateralHypergeometricPFQ ▪ EllipticK ▪ EllipticF ▪ EllipticE ▪ EllipticPi ▪ CarlsonRF ▪ CarlsonRK ▪ JacobiSN ▪ InverseJacobiSN ▪ WeierstrassP ▪ EllipticTheta ▪ DedekindEta ▪ KleinInvariantJ ▪ ModularLambda ▪ SiegelTheta ▪ Zeta ▪ PolyLog ▪ LerchPhi ▪ RiemannSiegelZ ▪ MathieuS ▪ MathieuSPrime ▪ MathieuC ▪ MathieuCharacteristicA ▪ SpheroidalPS ▪ SpheroidalS1 ▪ SpheroidalEigenvalue ▪ HeunG ▪ HeunC ▪ HeunB ▪ HeunD ▪ HeunT ▪ CoulombF ▪ CoulombG ▪ CoulombH1 ▪ CoulombH2 ▪ QFactorial ▪ QPochhammer ▪ QHypergeometricPFQ ▪ MittagLefflerE ▪ ProductLog ▪ InverseErf ▪ InverseGammaRegularized ▪ InverseEllipticNomeQ ▪ InverseWeierstrassP ▪ BesselJZero ▪ ZetaZero ▪ Root ▪ DifferentialRoot ▪ DifferenceRoot ▪ Derivative ▪ FindRoot ▪ Min ▪ Max ▪ RealAbs ▪ Piecewise ▪ Log ▪ Log10 ▪ Log2 ▪ Exp ▪ Power ▪ Sqrt ▪ CubeRoot ▪ Surd ▪ Degree ▪ Sin ▪ Cos ▪ Tan ▪ ArcSin ▪ ArcCos ▪ ArcTan ▪ Sinc ▪ Sinh ▪ Cosh ▪ Tanh ▪ ArcSinh ▪ ArcCosh ▪ ArcTanh ▪ N ▪ FunctionExpand ▪ FullSimplify ▪ Series ▪