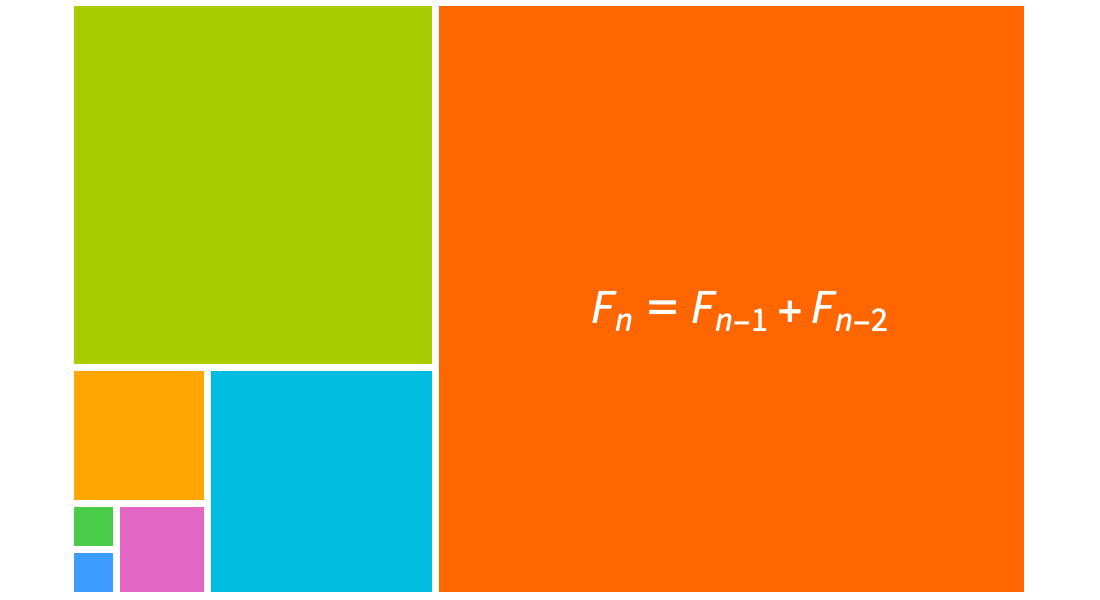Wolfram数学関数WOLFRAM言語の
コアとなる部分

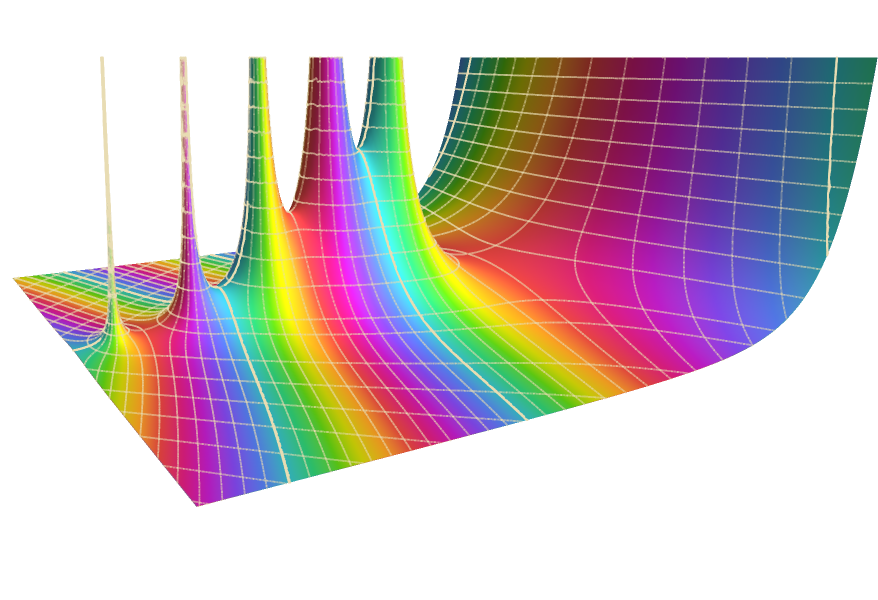
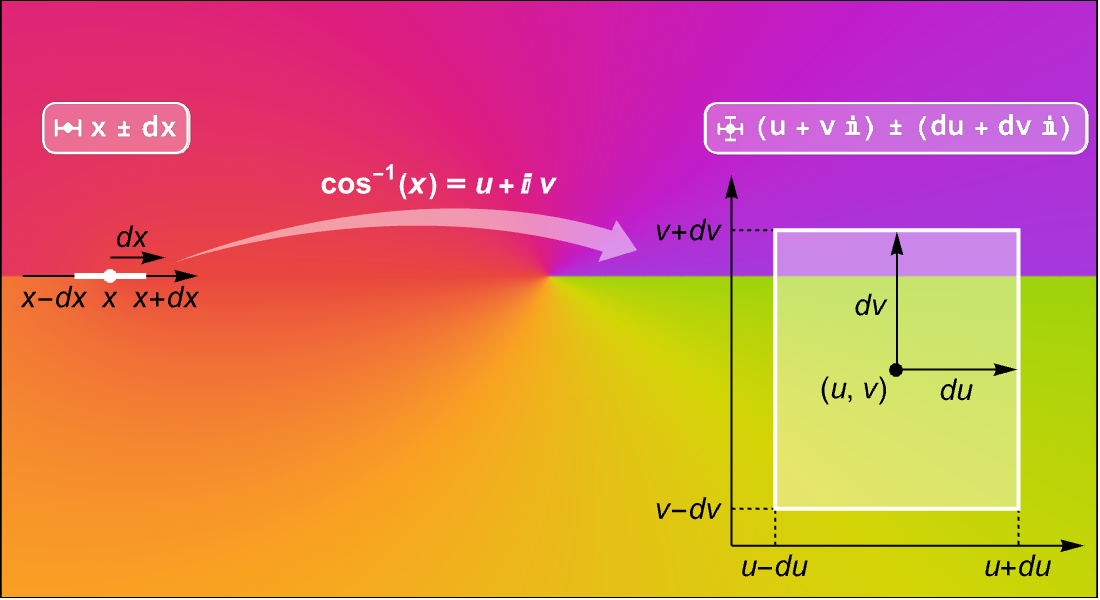
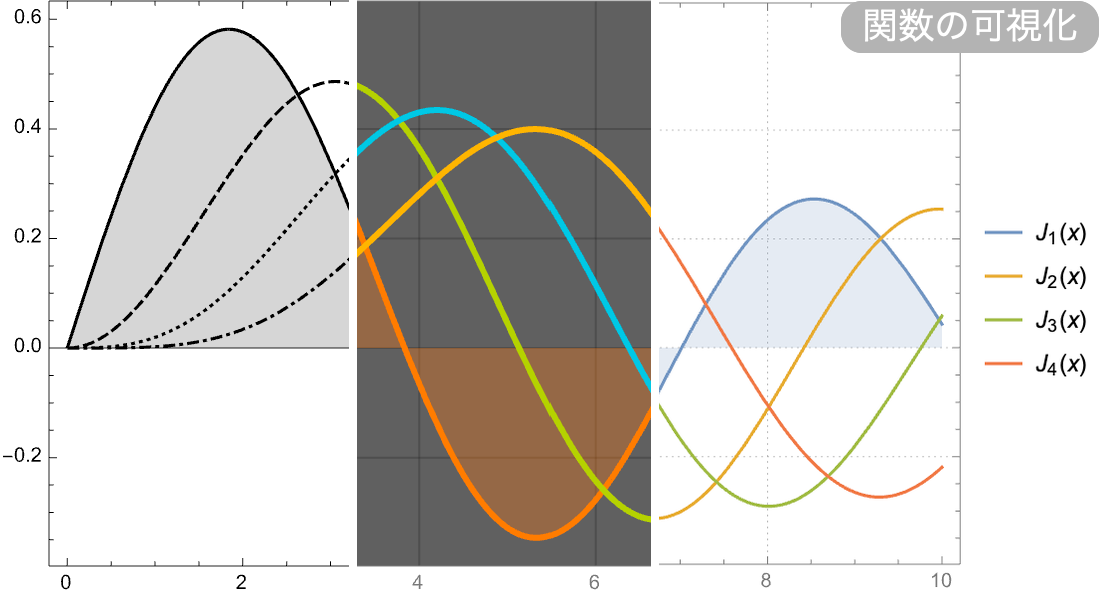
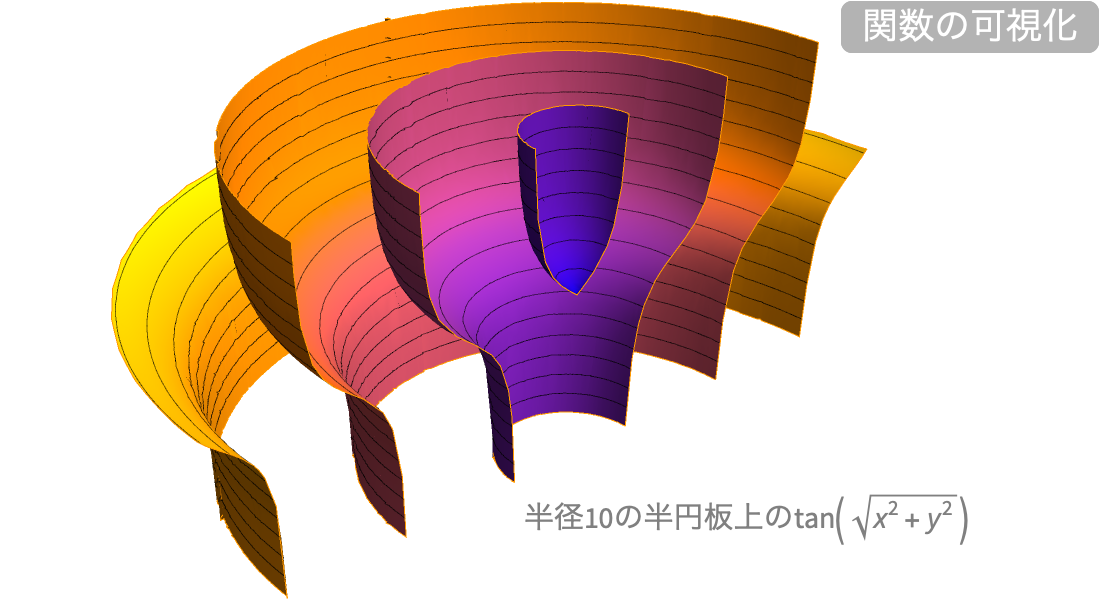
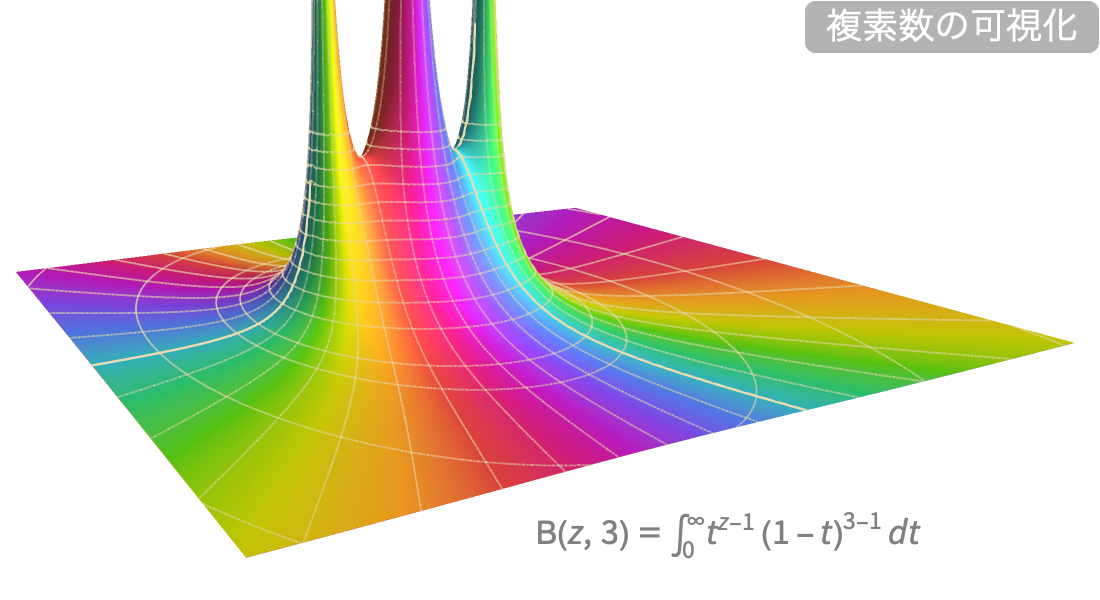
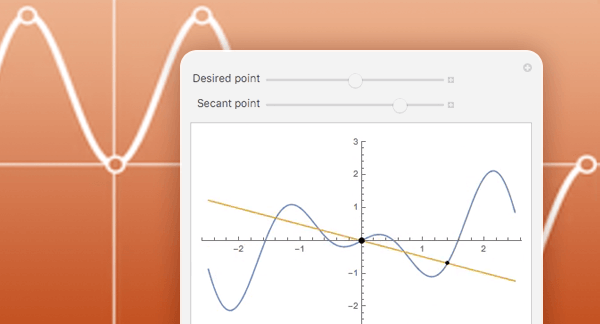
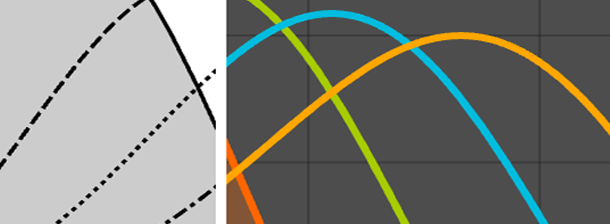
定義，計算，可視化

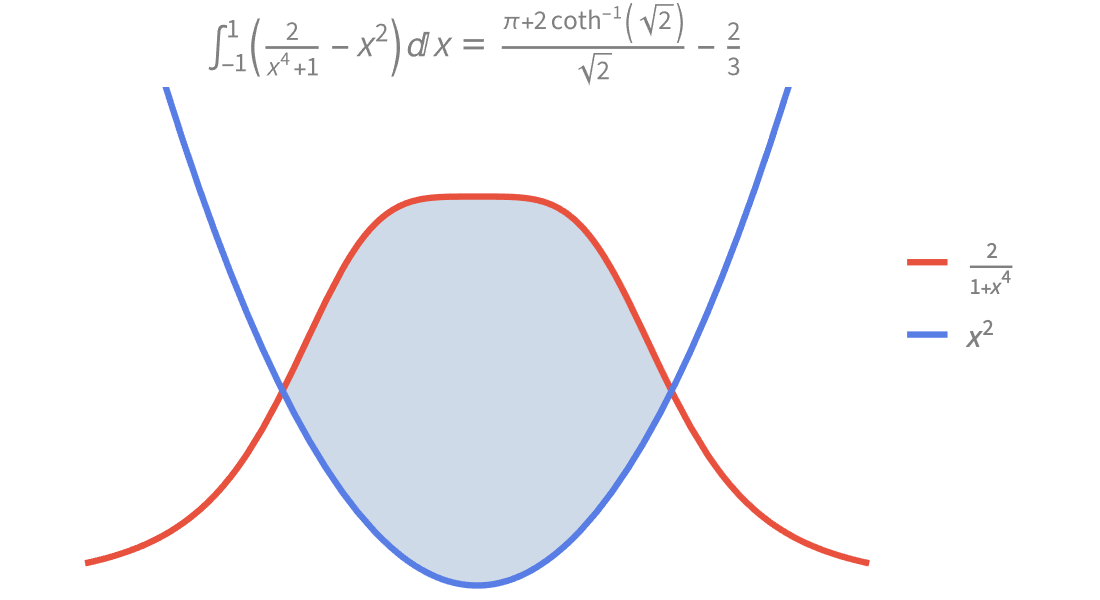
大規模な数学関数のコレクションの記号・数値評価，可視化，漸近展開等はどれも詳しく文書化されており，Wolfram言語のあらゆる部分と緊密に統合されています．

最大で完全なコレクション

初等関数から高度な特殊関数まで何百もの関数を含む幅広い関数コレクションは，記号および数値のソルバと緊密に統合されています．期待する精度まで数値結果を計算したり，式を求めたり簡約したりすることができます．さまざまなレベルに対応した詳しくインタラクティブなドキュメントによって，誰でも関数を活用することができます．

初等関数

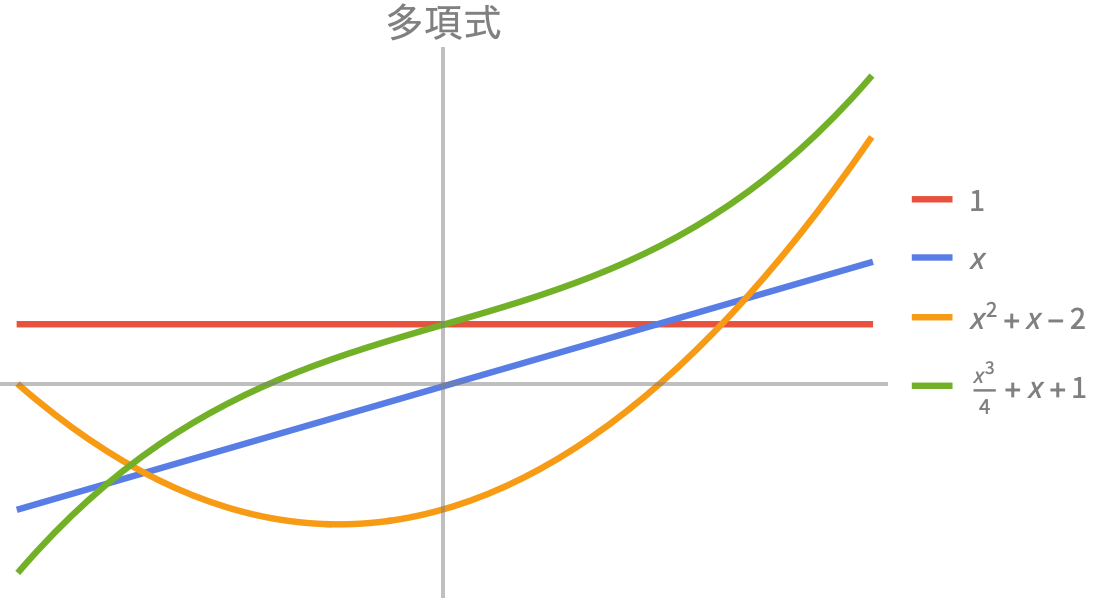
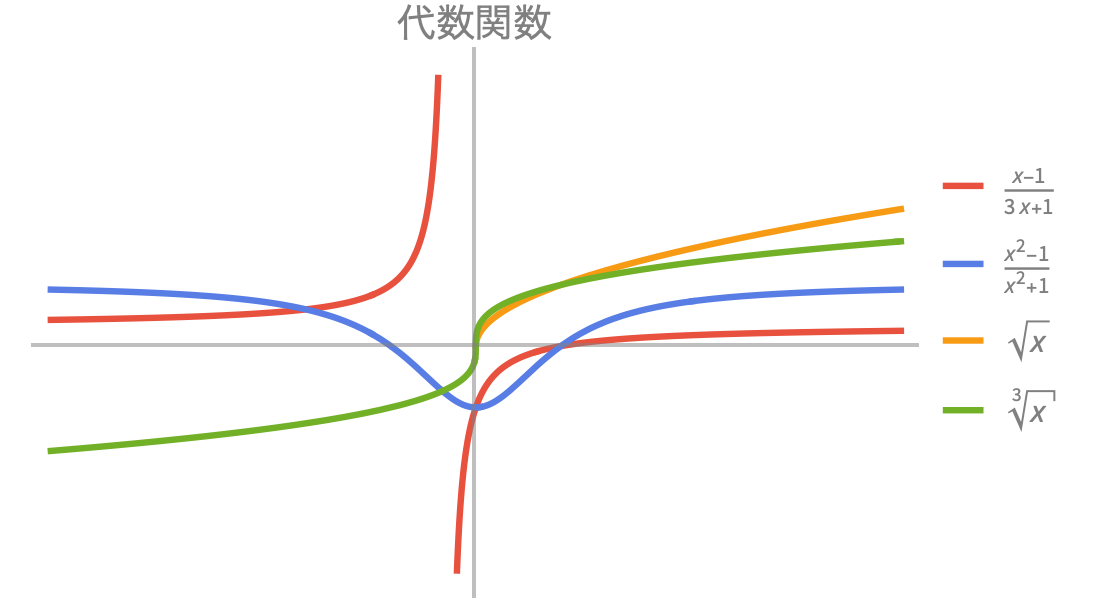
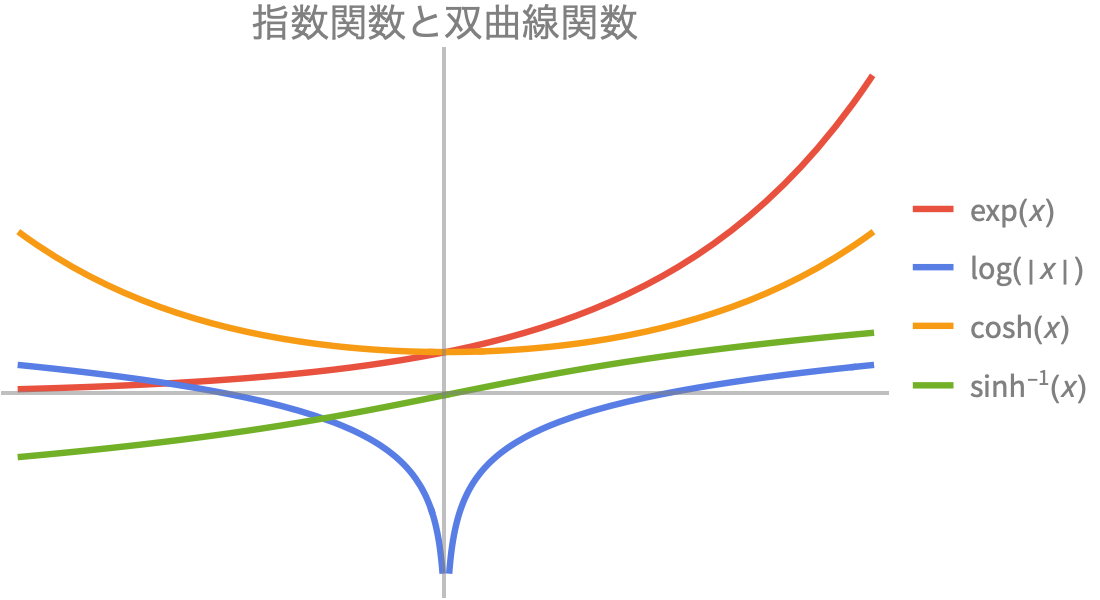
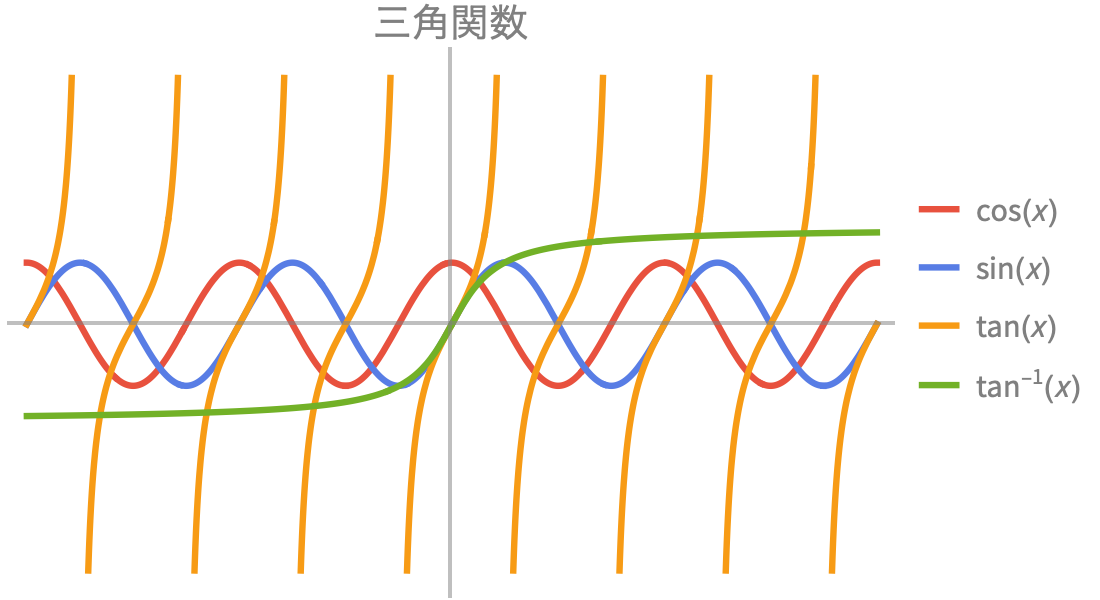
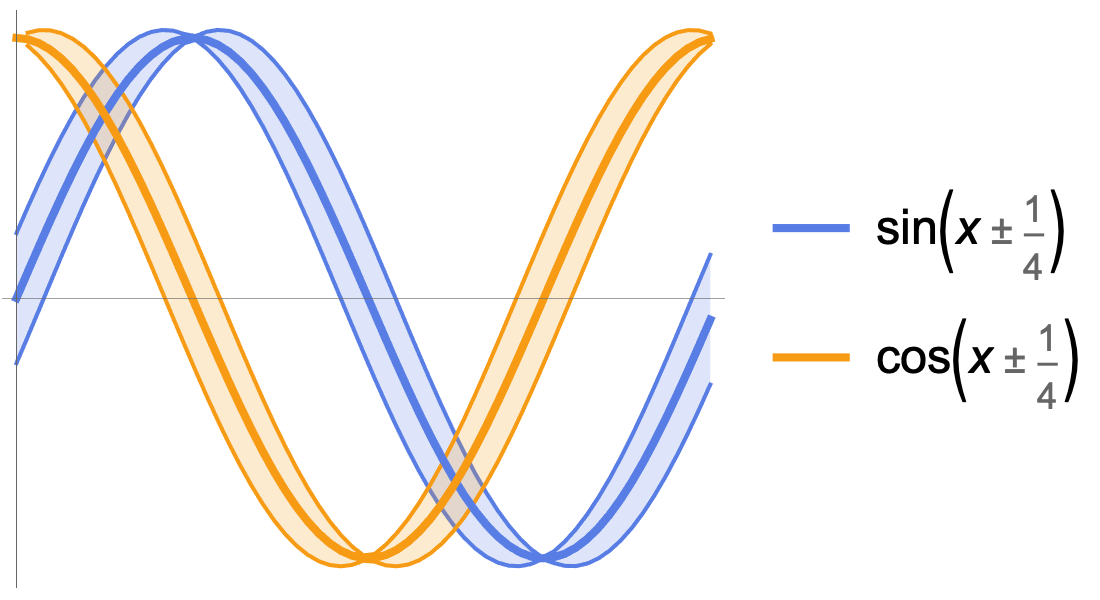
科学や工学での使用のために高速で正確な数値計算・記号計算を提供します．組込みの指数関数，三角関数，双曲線関数で，成長，減衰，振動挙動の組合せをモデル化することができます．

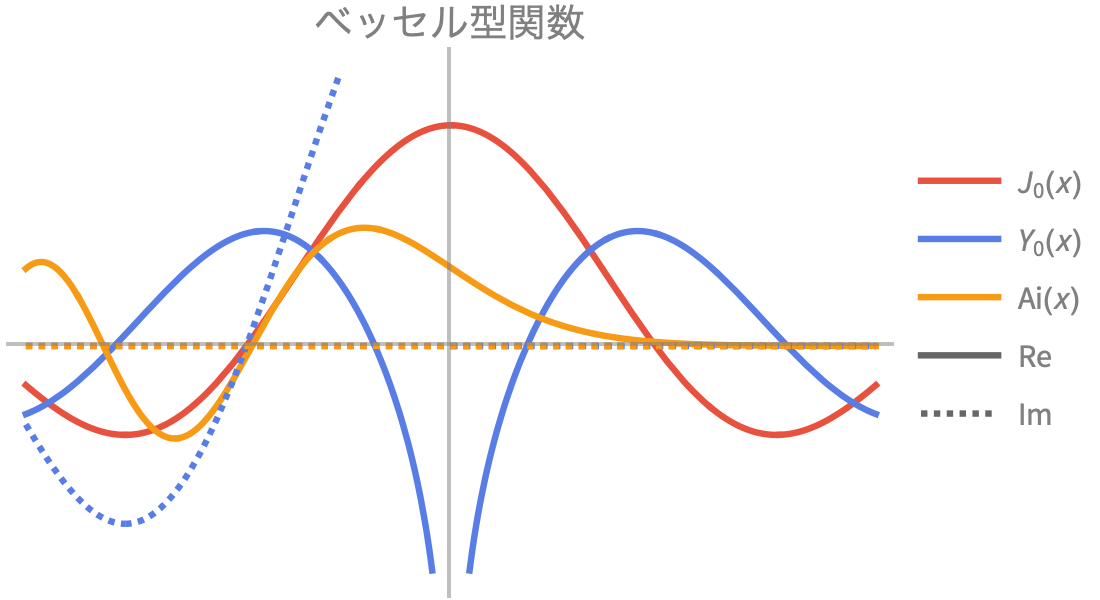
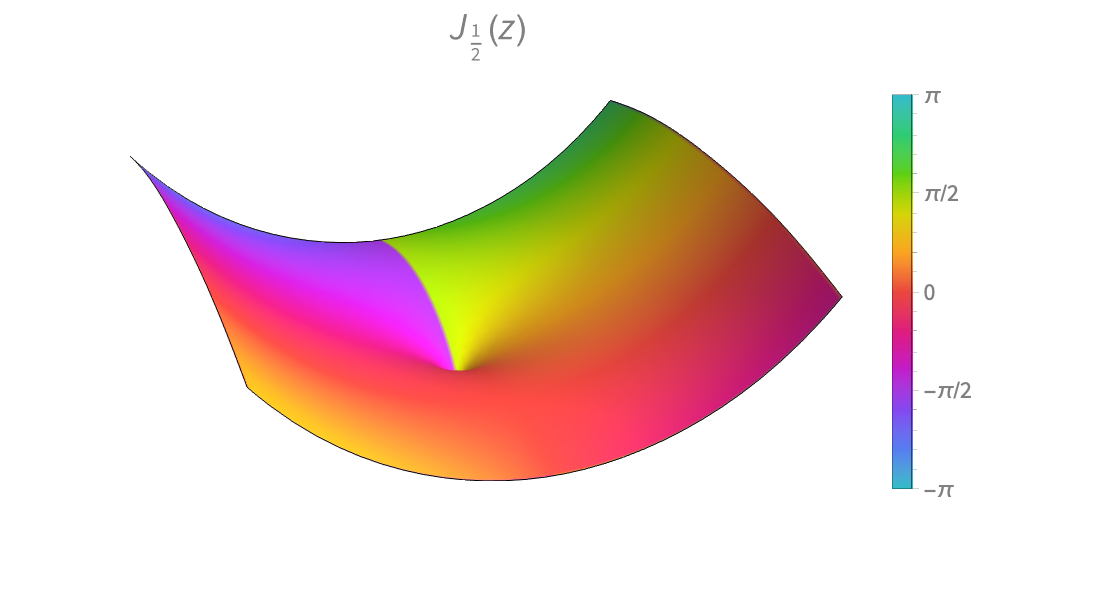
特殊関数

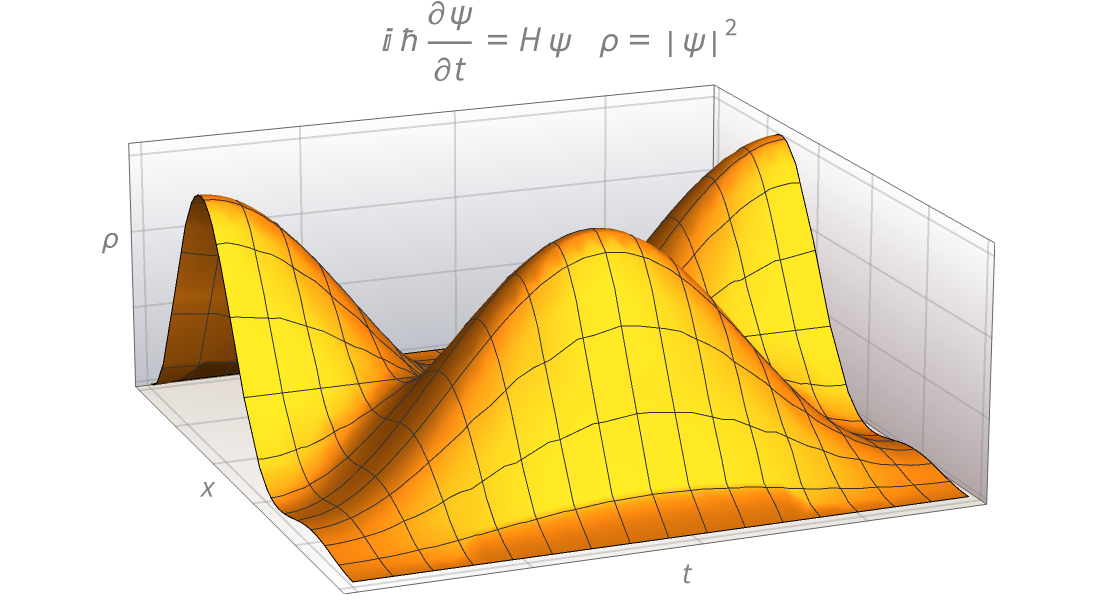
高精度の数値・記号級数展開を使って，物理学，工学，確率と統計の問題を解きます．

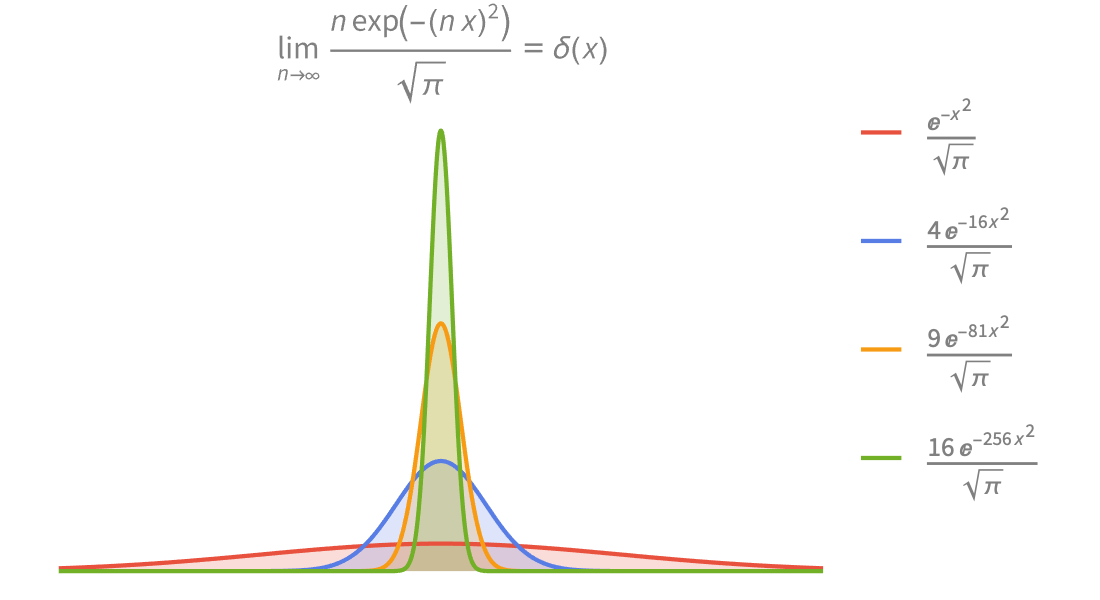
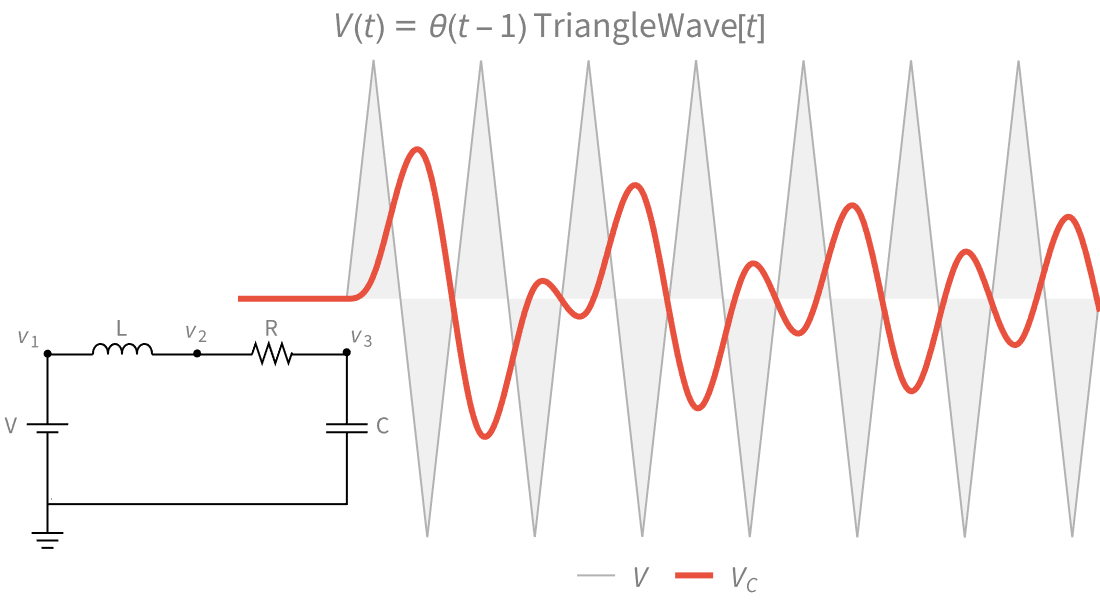
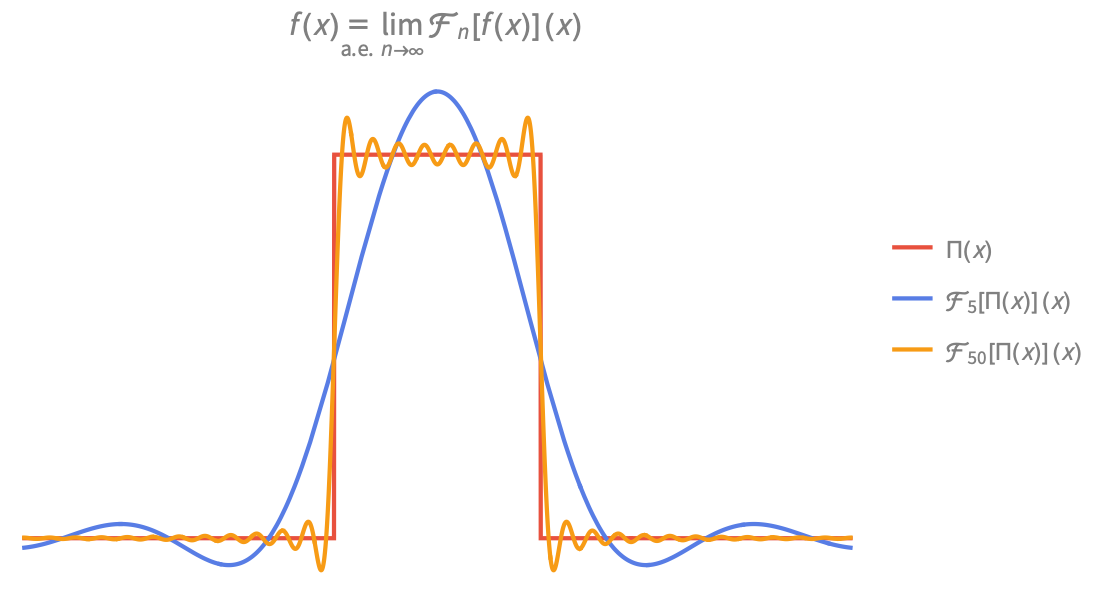
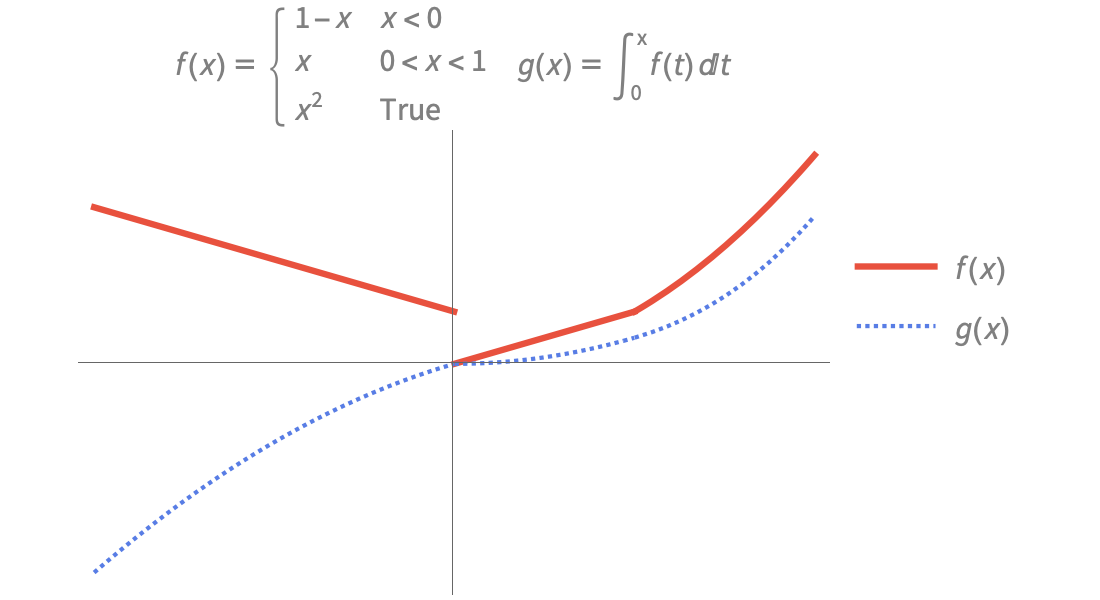
区分関数と一般化された関数

点ごとに定義され，広範に渡る区分関数および一般化された関数を使って，工学システムや物理システムをモデル化します．Piecewiseを使って独自の関数を作ることもできます．

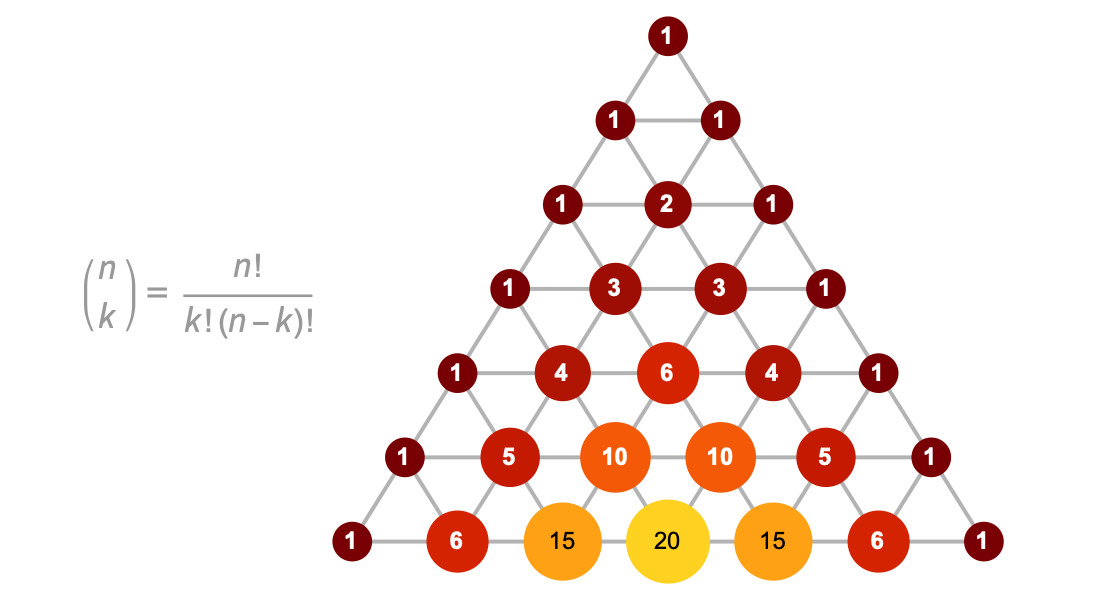
整数関数

二項係数，フィボナッチ数，調和数その他の整数関数を使って数列や級数を調べることができます．組込みの記号総和，再帰方程式の求解，数列認識を使って，組合せ論，アルゴリズム理論，その他の領域の問題が解けます．

関数の特性

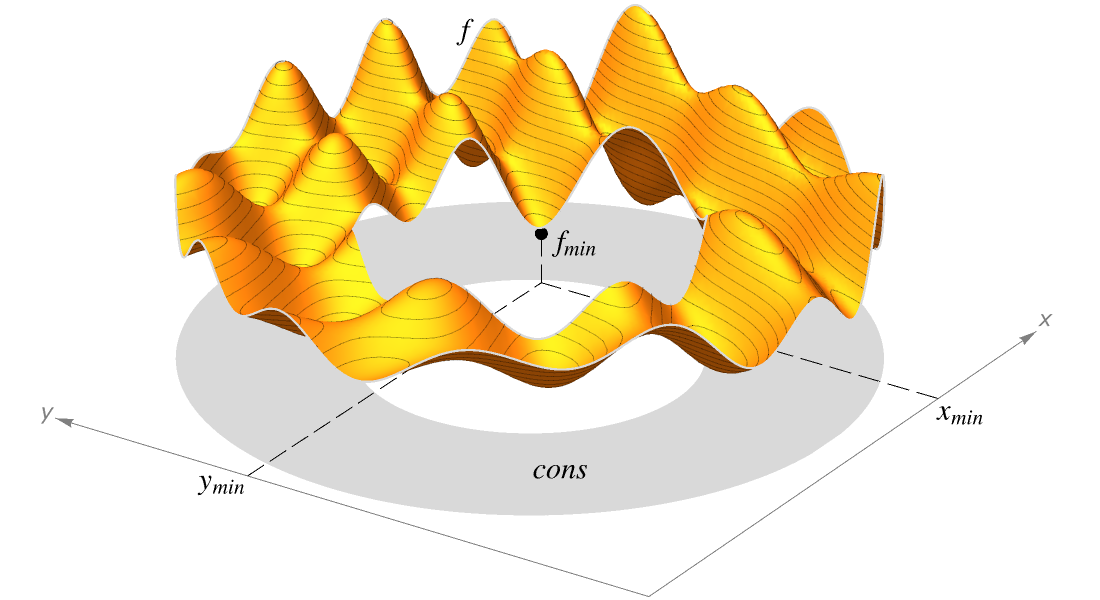
関数およびその総和，積，合成について15以上の重要な数学特性をすぐに計算し，多数の手順の数学的妥当性を確かめます．

記号計算

積分，微分方程式，その他多数の問題に対して最適な閉じた形式の解が得られます．式を簡約して厳密な答を得たり，包括的な数学関数の集合を使って問題を記号ソルバに正確で簡潔に入力したりできます．

数値計算

どのような数学関数の値でも，機械精度あるいは任意精度で計算できます．実数直線上および複素平面上のどちらでも，区間を使った厳密な境界で計算できます．統計の不確かさを簡単に伝搬したり，任意の関数を使って数値ソルバに問題を正確に入力したりできます．

漸近計算

厳密な記号評価ができず，数値評価の信頼性が低い場合，問題の記号解析のために関数の漸近近似が計算できます．級数についての強力なシステムのおかげで，入力でどのような解析関数も使うことができ，必要とされる数学関数を使い続けることで，一般化された級数は結果を簡潔に表すことができます．

可視化

レポートや論文のために高品質の図表を作成し，数学関数の挙動を見ることができます．

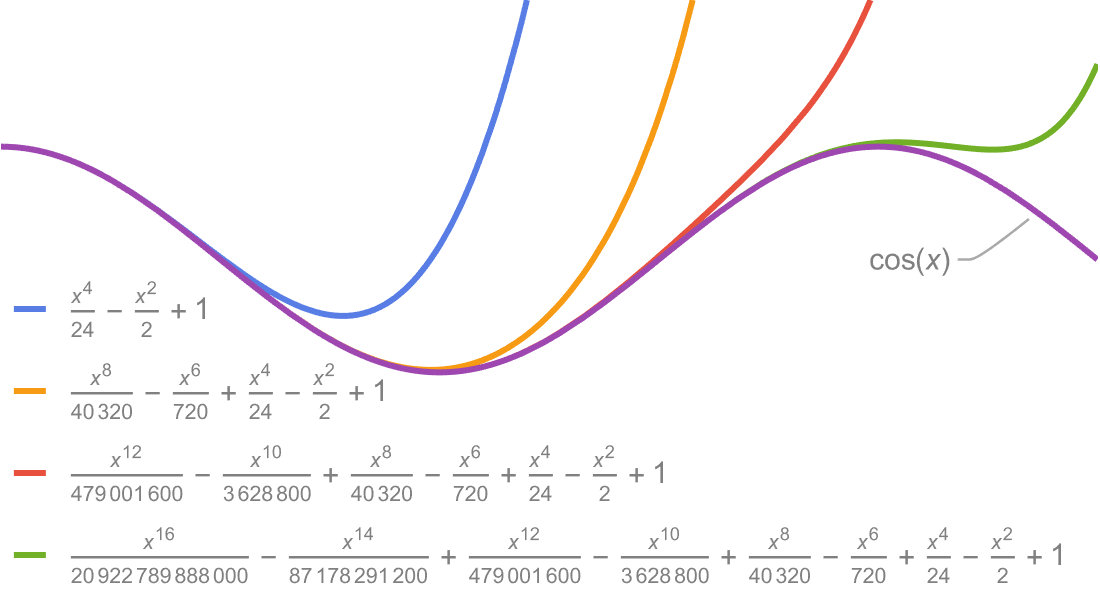
数学関数に関するWolframドキュメント

Wolfram 数学関数は，Wolfram言語に統合されています．全システムに計算の全分野を網羅する6,000個を超える組込み関数が含まれており，そのすべてが綿密に統合されているため，完全に一体となって作動します．

Pi ▪ E ▪ EulerGamma ▪ I ▪ Re ▪ Im ▪ Conjugate ▪ Arg ▪ Plus ▪ Times ▪ Total ▪ Abs ▪ Round ▪ Floor ▪ Clip ▪ Ramp ▪ Rescale ▪ DiracDelta ▪ HeavisideTheta ▪ DiracComb ▪ Mod ▪ Quotient ▪ Divisible ▪ GCD ▪ Factorial ▪ Binomial ▪ Fibonacci ▪ BernoulliB ▪ StirlingS1 ▪ IntegerDigits ▪ DigitCount ▪ BitAnd ▪ FactorInteger ▪ Prime ▪ PrimePi ▪ EulerPhi ▪ MoebiusMu ▪ DivisorSigma ▪ JacobiSymbol ▪ MultiplicativeOrder ▪ PartitionsP ▪ SquaresR ▪ DirichletL ▪ FunctionInjective ▪ FunctionSign ▪ FunctionSingularities ▪ NormalDistribution ▪ ChiSquareDistribution ▪ PoissonDistribution ▪ RandomInteger ▪ RandomReal ▪ RandomChoice ▪ RandomPrime ▪ SquareWave ▪ TriangleWave ▪ UnitBox ▪ MandelbrotSetMemberQ ▪ JuliaSetIterationCount ▪ CantorStaircase ▪ MathematicalFunctionData ▪ Gamma ▪ Pochhammer ▪ Beta ▪ PolyGamma ▪ LogGamma ▪ Erf ▪ Erfc ▪ ExpIntegralE ▪ ExpIntegralEi ▪ LogIntegral ▪ FresnelS ▪ SinIntegral ▪ HermiteH ▪ LaguerreL ▪ JacobiP ▪ GegenbauerC ▪ ChebyshevT ▪ ChebyshevU ▪ ZernikeR ▪ SphericalHarmonicY ▪ WignerD ▪ BesselJ ▪ BesselY ▪ BesselI ▪ BesselK ▪ AiryAi ▪ AiryAiPrime ▪ SphericalBesselJ ▪ KelvinBer ▪ HankelH1 ▪ StruveH ▪ LegendreP ▪ LegendreQ ▪ SpheroidalQS ▪ Hypergeometric2F1 ▪ HypergeometricPFQ ▪ HypergeometricU ▪ MeijerG ▪ FoxH ▪ AppellF1 ▪ BilateralHypergeometricPFQ ▪ EllipticK ▪ EllipticF ▪ EllipticE ▪ EllipticPi ▪ CarlsonRF ▪ CarlsonRK ▪ JacobiSN ▪ InverseJacobiSN ▪ WeierstrassP ▪ EllipticTheta ▪ DedekindEta ▪ KleinInvariantJ ▪ ModularLambda ▪ SiegelTheta ▪ Zeta ▪ PolyLog ▪ LerchPhi ▪ RiemannSiegelZ ▪ MathieuS ▪ MathieuSPrime ▪ MathieuC ▪ MathieuCharacteristicA ▪ SpheroidalPS ▪ SpheroidalS1 ▪ SpheroidalEigenvalue ▪ HeunG ▪ HeunC ▪ HeunB ▪ HeunD ▪ HeunT ▪ CoulombF ▪ CoulombG ▪ CoulombH1 ▪ CoulombH2 ▪ QFactorial ▪ QPochhammer ▪ QHypergeometricPFQ ▪ MittagLefflerE ▪ ProductLog ▪ InverseErf ▪ InverseGammaRegularized ▪ InverseEllipticNomeQ ▪ InverseWeierstrassP ▪ BesselJZero ▪ ZetaZero ▪ Root ▪ DifferentialRoot ▪ DifferenceRoot ▪ Derivative ▪ FindRoot ▪ Min ▪ Max ▪ RealAbs ▪ Piecewise ▪ Log ▪ Log10 ▪ Log2 ▪ Exp ▪ Power ▪ Sqrt ▪ CubeRoot ▪ Surd ▪ Degree ▪ Sin ▪ Cos ▪ Tan ▪ ArcSin ▪ ArcCos ▪ ArcTan ▪ Sinc ▪ Sinh ▪ Cosh ▪ Tanh ▪ ArcSinh ▪ ArcCosh ▪ ArcTanh ▪ N ▪ FunctionExpand ▪ FullSimplify ▪ Series ▪