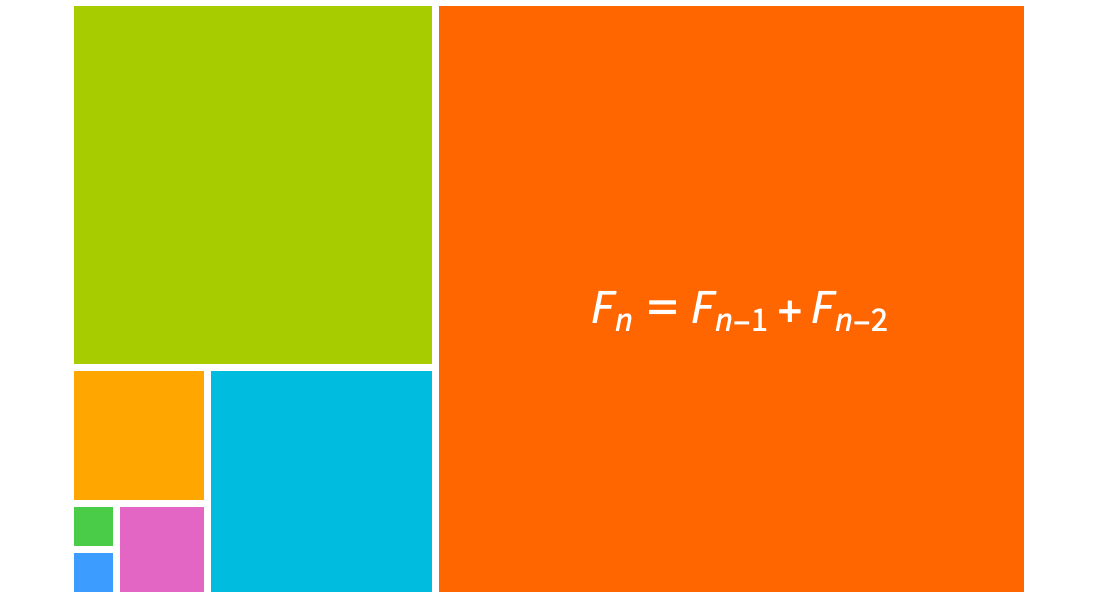WolframFunções MatemáticasPARTE CENTRAL DA
WOLFRAM LANGUAGE

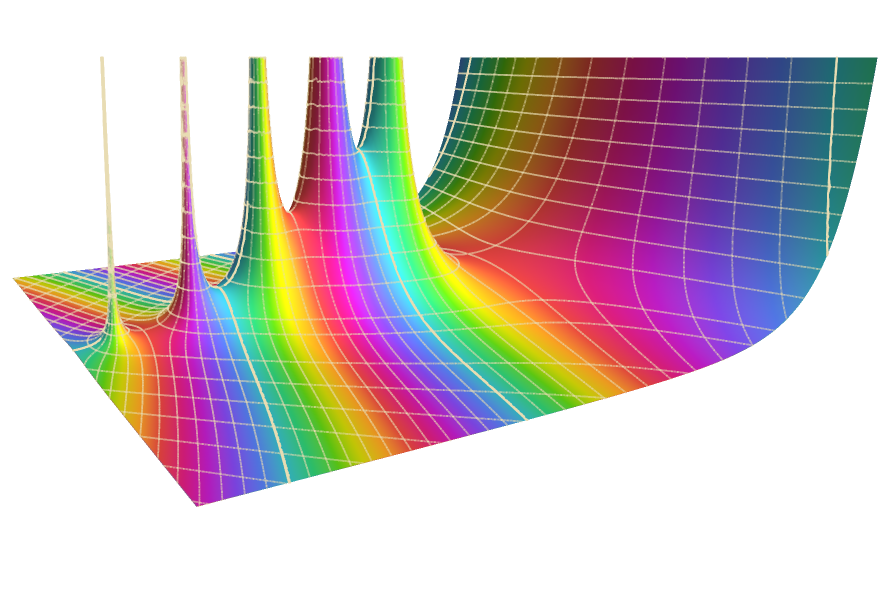
Defina, calcule e visualize.

Avaliação simbólica e numérica, visualização e expansões assintóticas de uma grande coleção de funções matemáticas — extensivamente documentadas e intimamente integradas a todas as áreas da Wolfram Language.

Comece agora mesmo

Coleção Mais Completa

Com centenas de funções especiais, desde elementares até avançadas, esta ampla coleção está integrada de forma coesa em solucionadores simbólicos e numéricos. Calcule resultados numéricos com a precisão desejada e encontre ou simplifique fórmulas. A documentação extensa, em vários níveis e interativa, permite que qualquer pessoa aproveite seu poder.

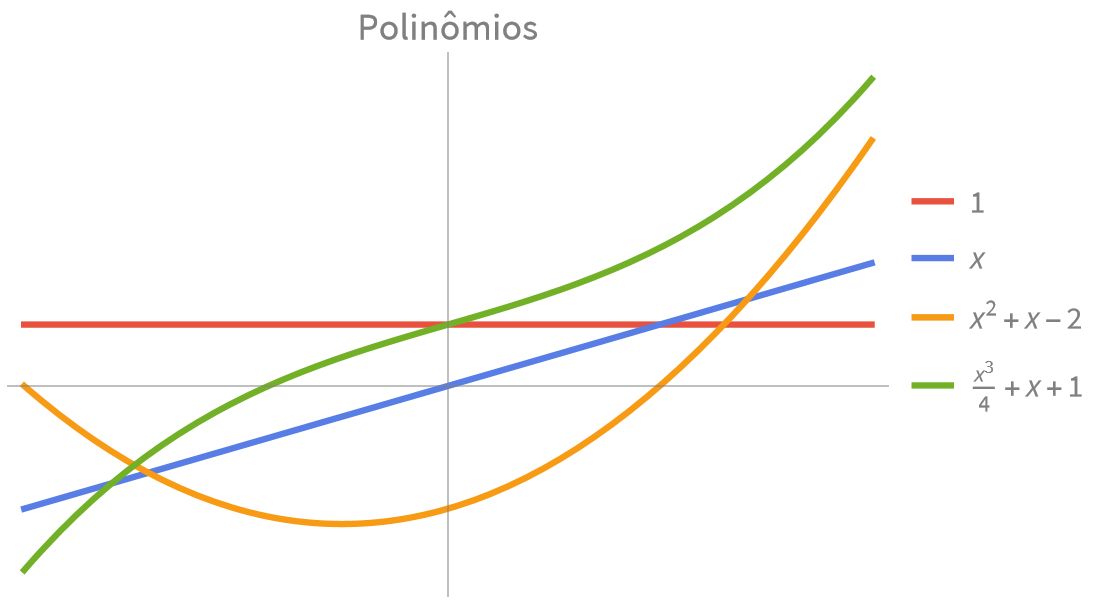
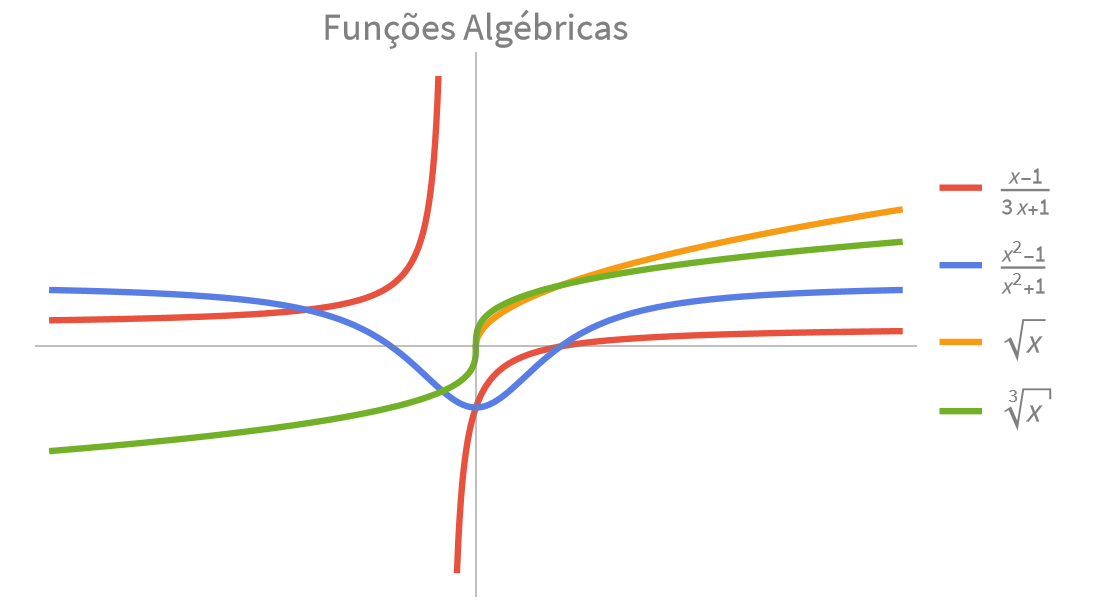
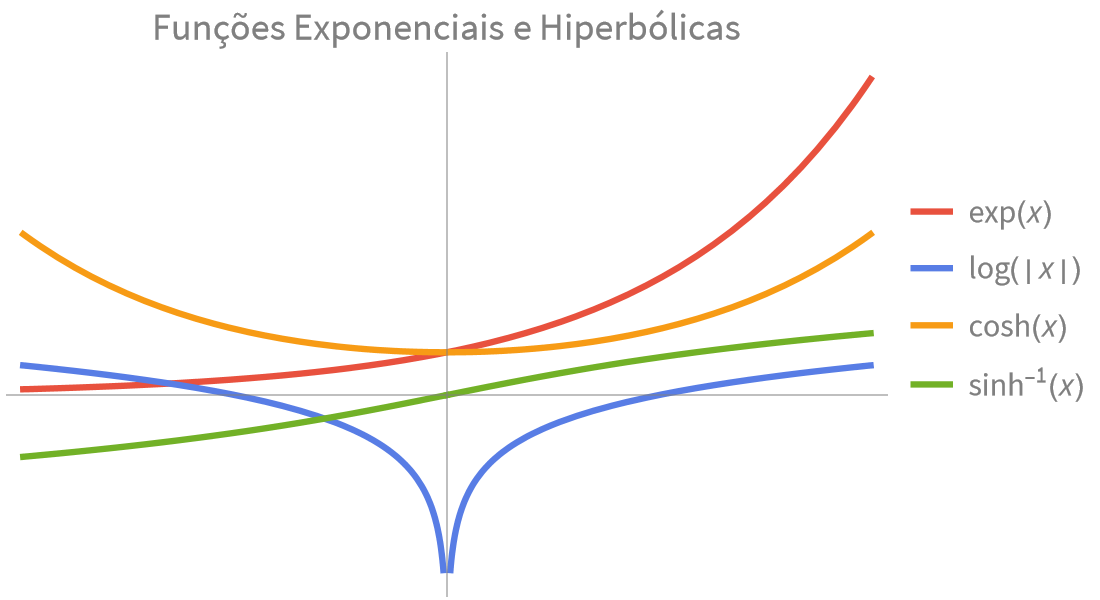
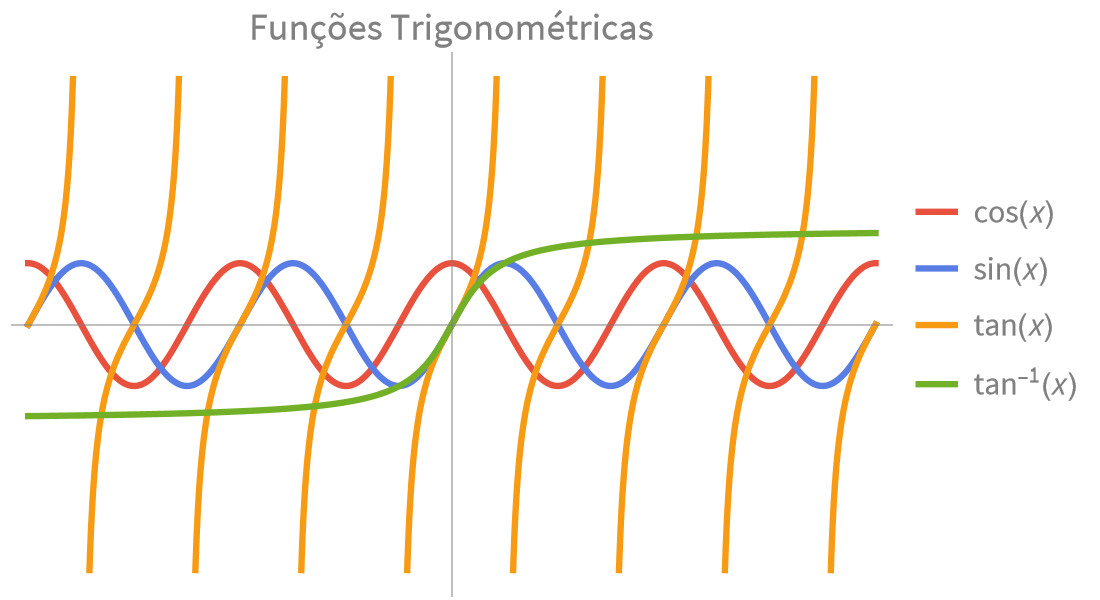
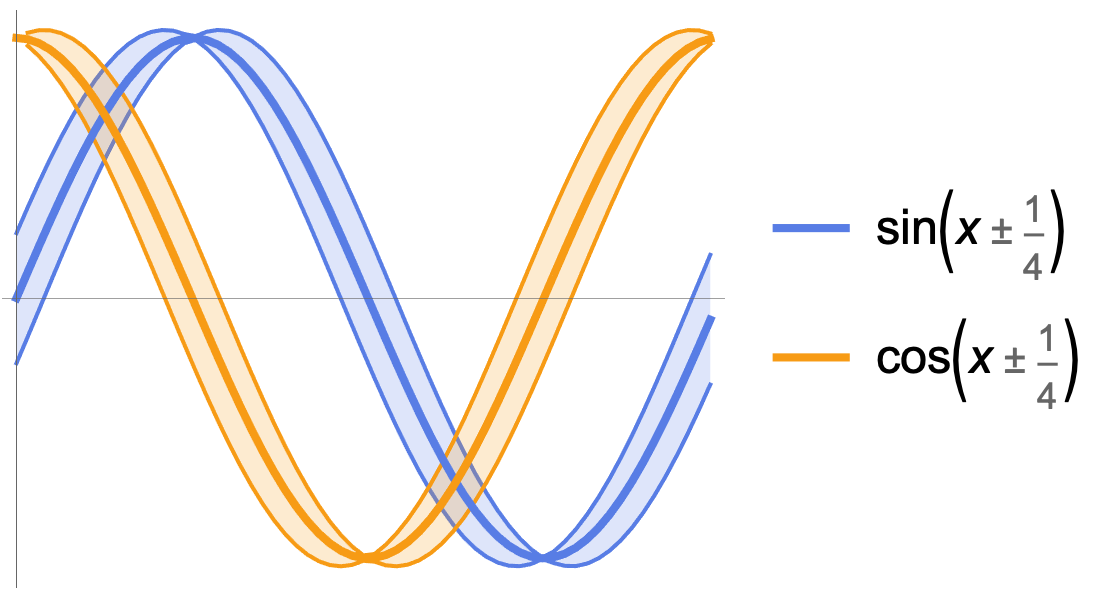
Funções Elementares

Cálculos numéricos e simbólicos rápidos e precisos para aplicações científicas e de engenharia. Funções exponenciais, trigonométricas e hiperbólicas incorporadas para modelar combinações de crescimento, decaimento e comportamento oscilatório.

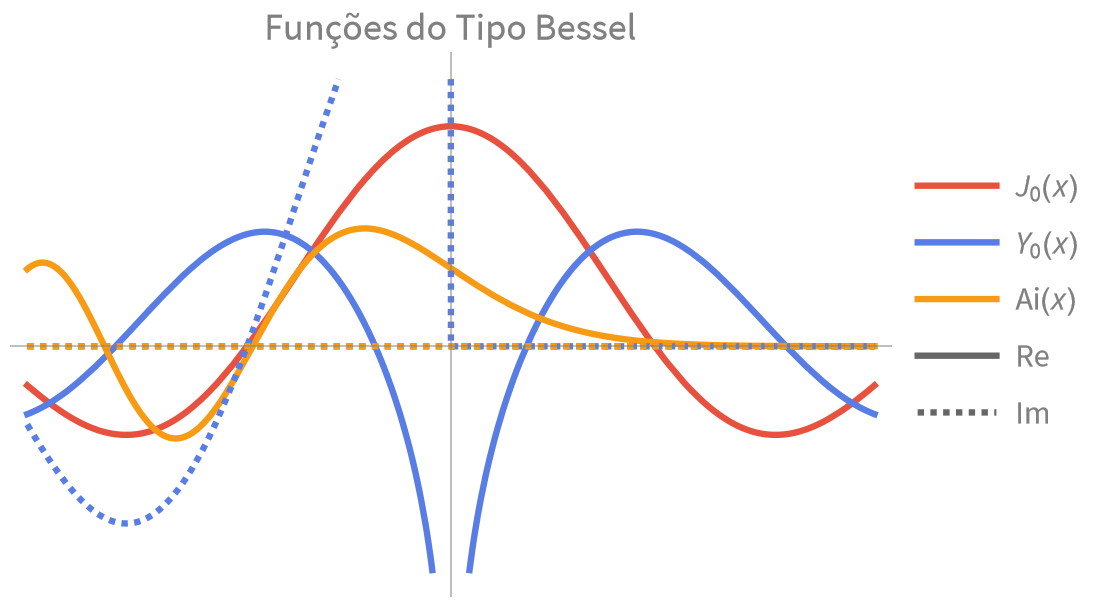
Funções Especiais

Resolva problemas em física, engenharia, probabilidade e estatística com numéricos de alta precisão ou expansão simbólica em séries.

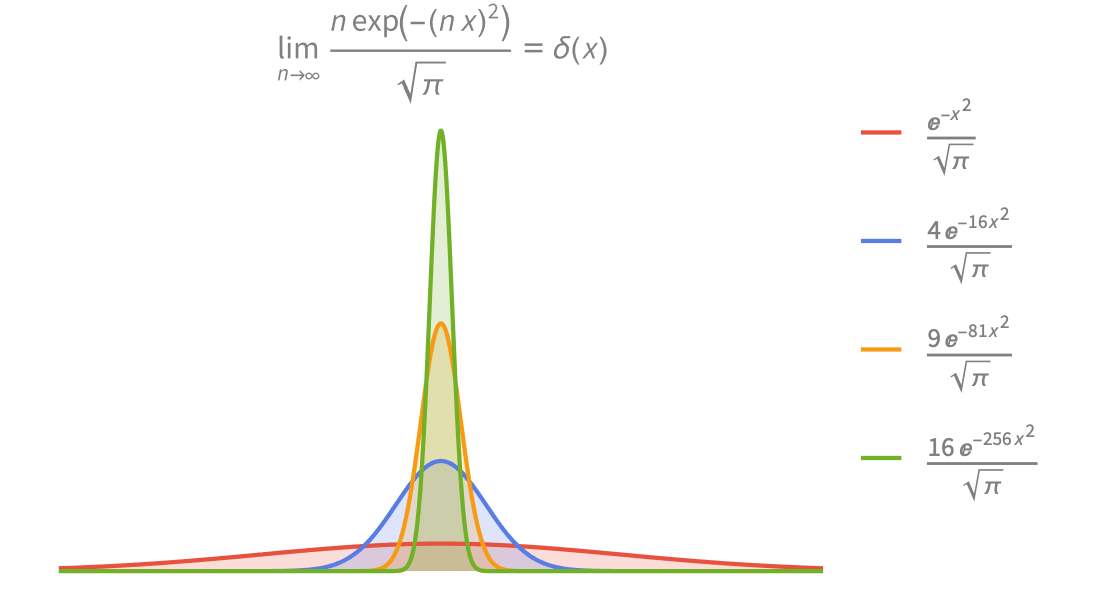
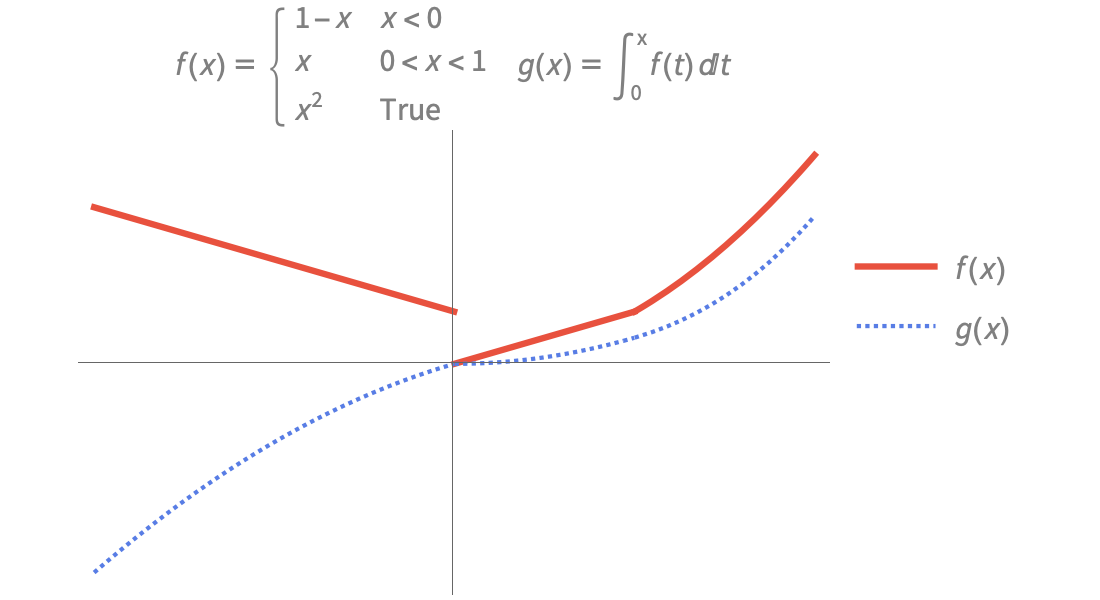
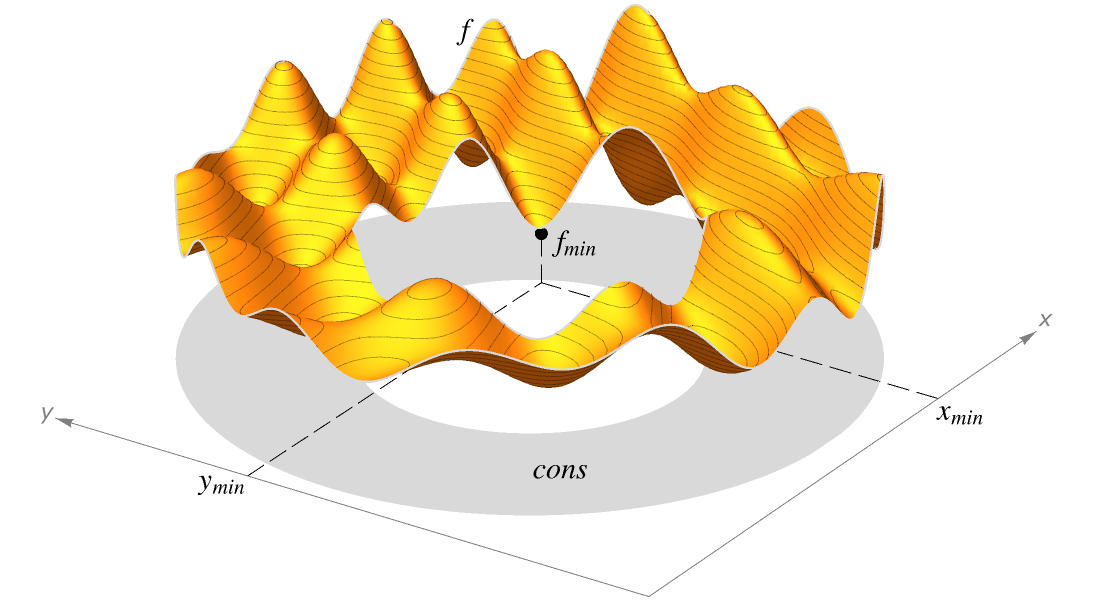
Funções Piecewise e Funções Generalizadas

Modele sistemas de engenharia e física com uma ampla gama de funções definidas ponto a ponto e funções generalizadas. Construa suas próprias funções usando a função Piecewise.

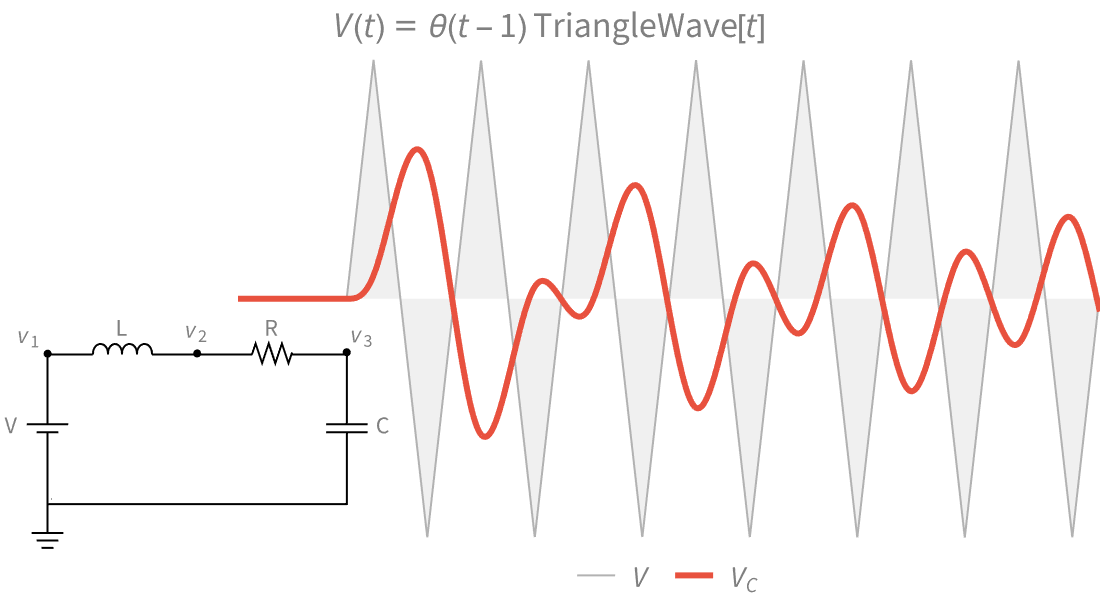
Funções Integrais

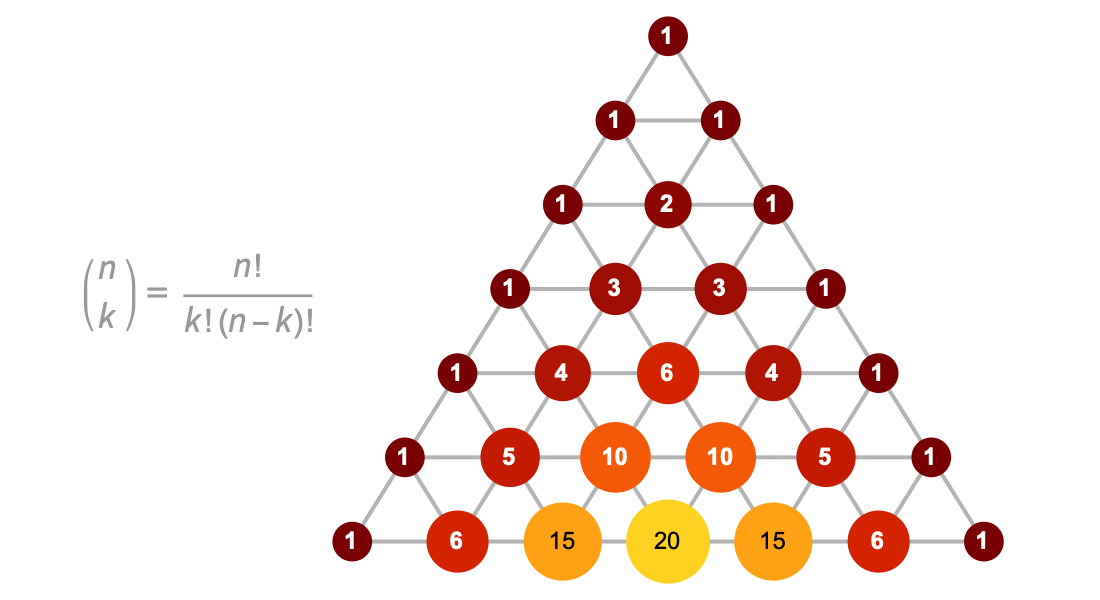
Explore sequências e séries com coeficientes binomiais, números de Fibonacci e harmônicos, bem como outras funções inteiras. Utilize somatórios simbólicos incorporados, resolução de equações de recorrência e reconhecimento de sequências para resolver problemas em combinatorics, a teoria de algoritmos e outros domínios.

Propriedades de Função

Calcule rapidamente mais de 15 propriedades matemáticas essenciais de funções e suas somas, produtos e composições para garantir a validade matemática de muitos procedimentos.

Computação Simbólica

Obtenha soluções em forma fechada de primeira classe para integrais, equações diferenciais e dezenas de outros problemas. Simplifique fórmulas e calcule respostas exatas. Insira problemas em solucionadores simbólicos de forma precisa e concisa, utilizando o conjunto abrangente de funções matemáticas.

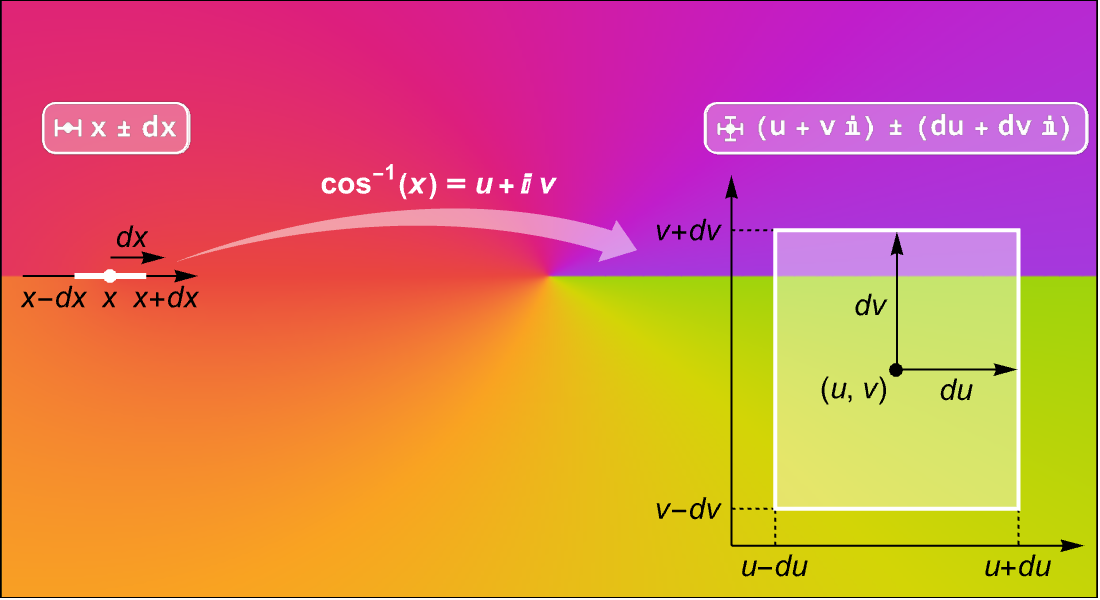
Cálculo Numérico

Calcule o valor de qualquer função matemática com precisão de máquina ou para uma precisão arbitrária especificada. Calcule com limites rigorosos usando intervalos, tanto na linha real quanto no plano complexo. Propague facilmente incertezas estatísticas. Insira problemas em solucionadores numéricos com precisão usando qualquer função desejada.

Cálculo Assintótico

Calcule aproximações assintóticas de funções para análise simbólica de problemas quando a avaliação simbólica exata falha e a avaliação numérica não é confiável. Um sistema robusto para séries permite que qualquer função analítica seja usada como entrada, e séries generalizadas podem expressar resultados de forma concisa, continuando a usar funções matemáticas necessárias.

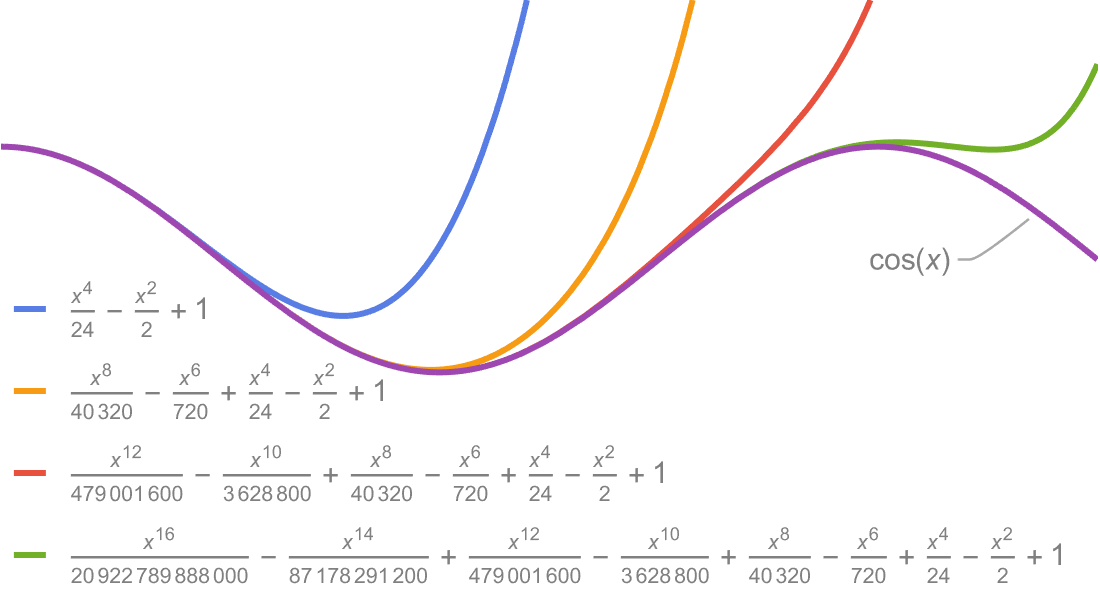
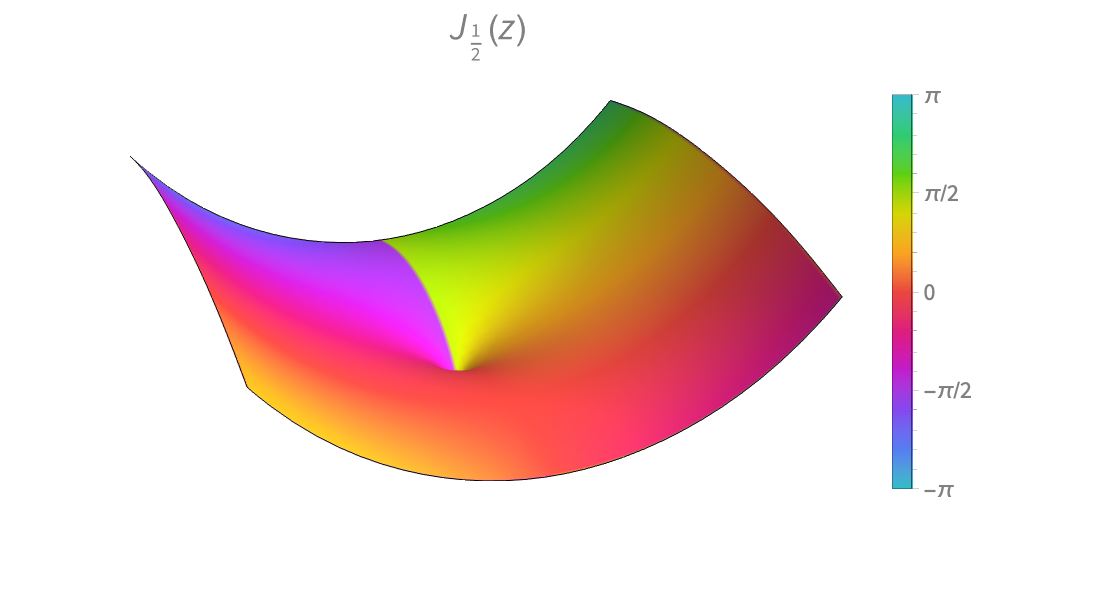
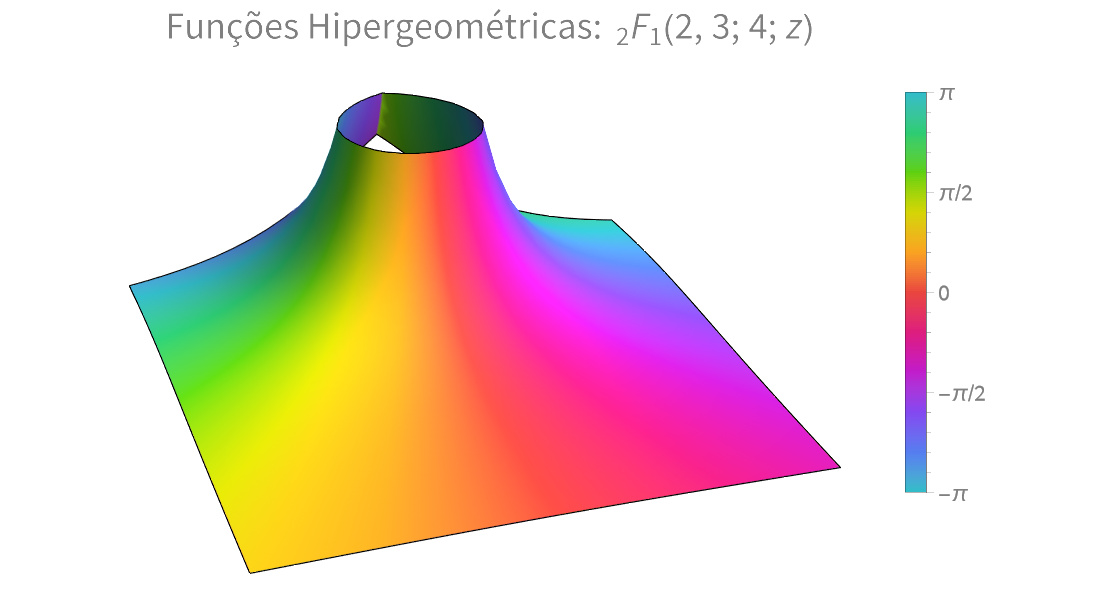
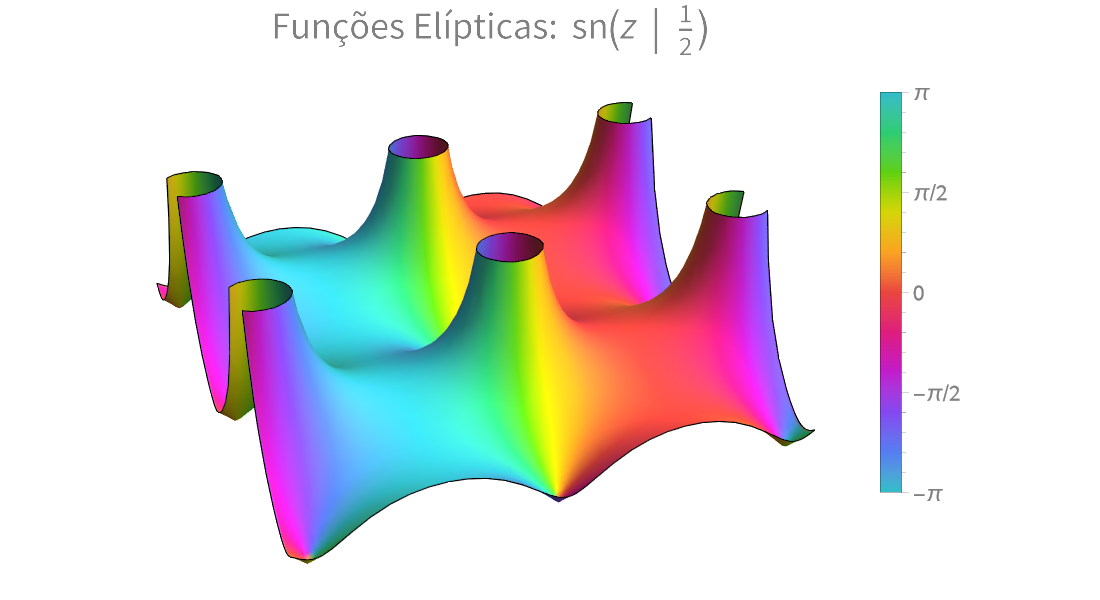
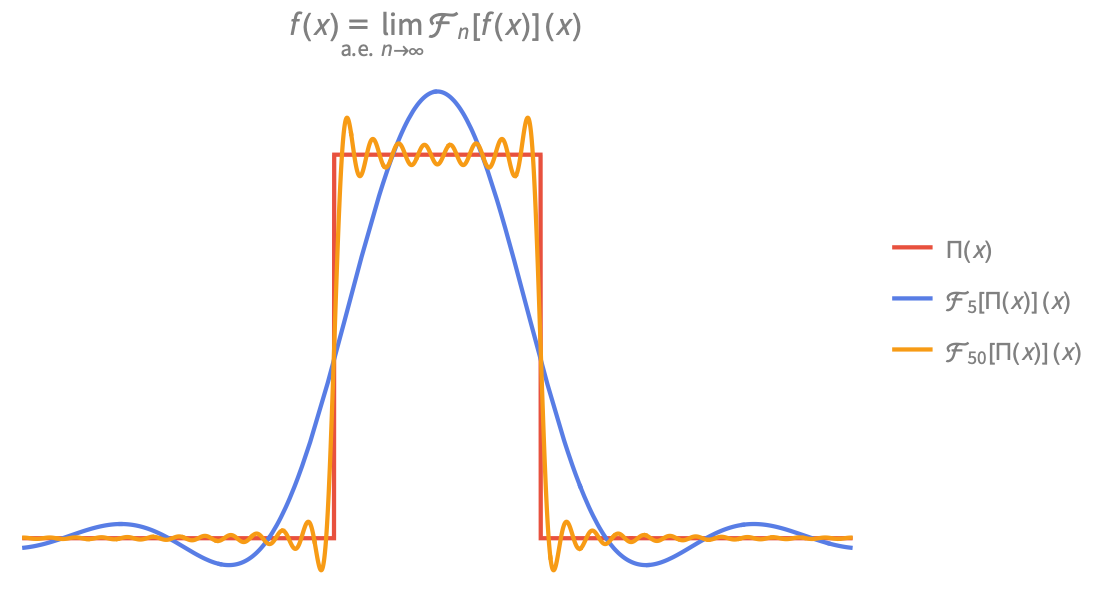
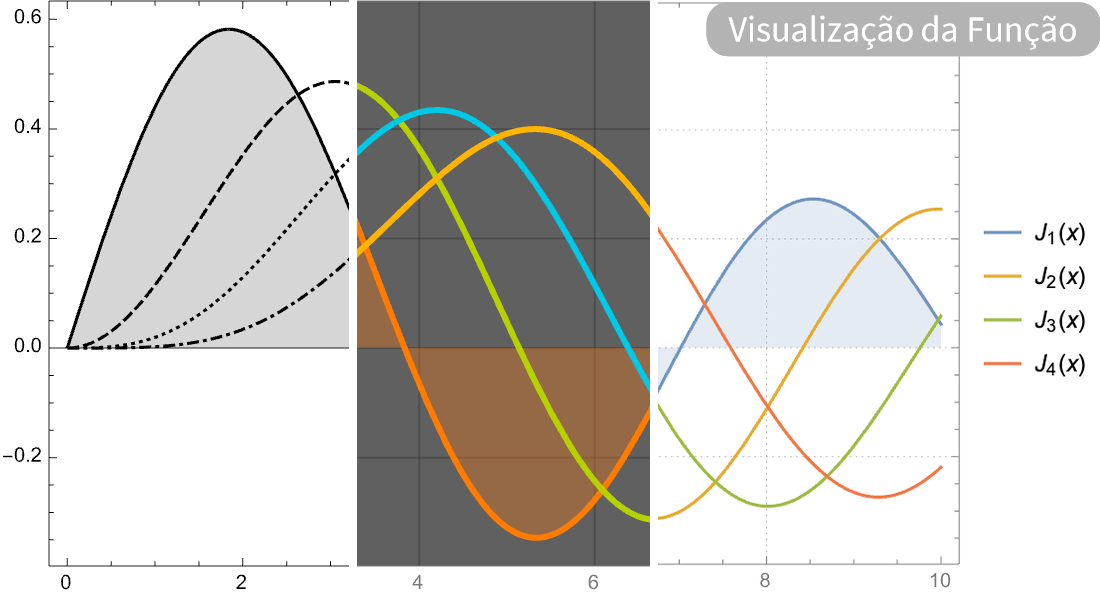
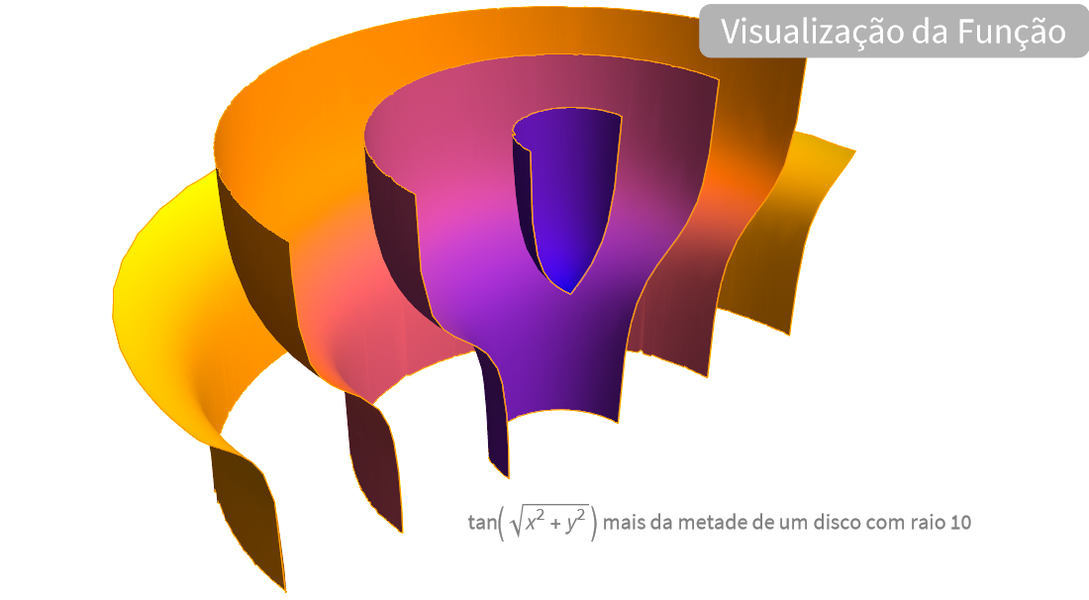
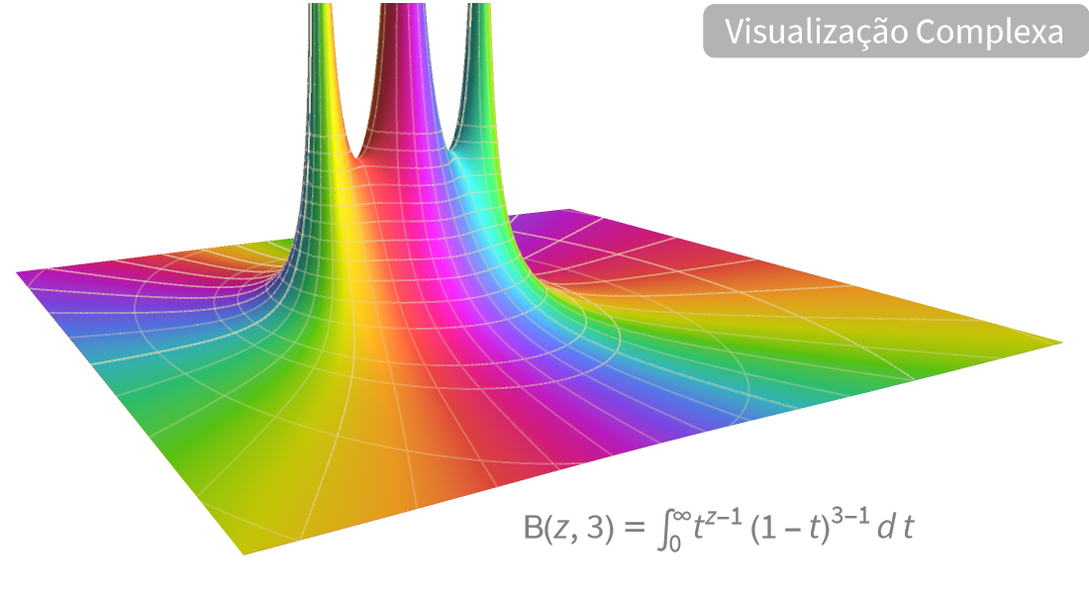
Visualização

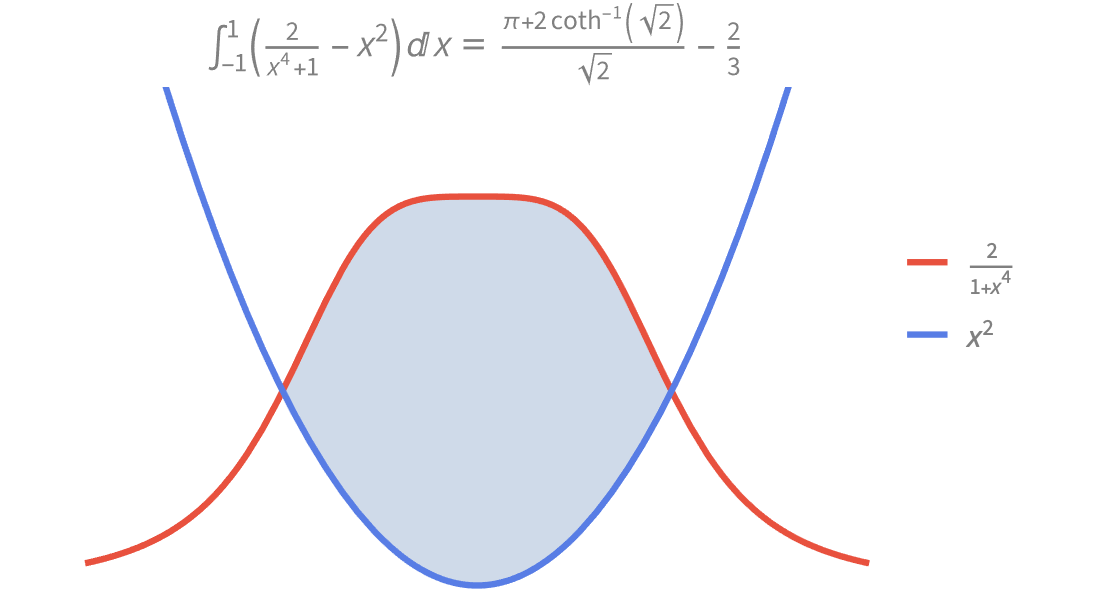
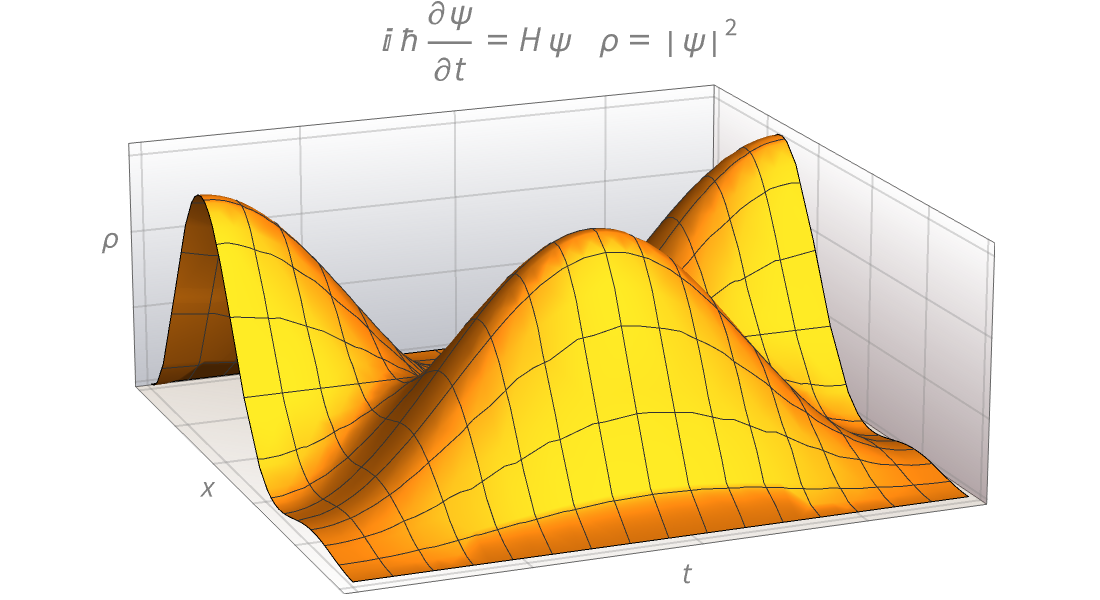
Produza ilustrações de alta qualidade para relatórios e trabalhos e obter insights sobre o comportamento de funções matemáticas.

Documentação para Wolfram Funções Matemáticas

Wolfram Funções Matemáticas é uma parte embutida da Wolfram Language. Todo o sistema contém mais de 6 mil funções integradas, abrangendo todas as áreas da computação — tudo cuidadosamente integrado para que funcione perfeitamente em conjunto.

Wolfram Language
Escopo Completo & Documentação

Guide

Guia para Funções Elementares

Guide

Guia para Funções Especiais

Guide

Guia para Funções Matemáticas

Pi ▪ E ▪ EulerGamma ▪ I ▪ Re ▪ Im ▪ Conjugate ▪ Arg ▪ Plus ▪ Times ▪ Total ▪ Abs ▪ Round ▪ Floor ▪ Clip ▪ Ramp ▪ Rescale ▪ DiracDelta ▪ HeavisideTheta ▪ DiracComb ▪ Mod ▪ Quotient ▪ Divisible ▪ GCD ▪ Factorial ▪ Binomial ▪ Fibonacci ▪ BernoulliB ▪ StirlingS1 ▪ IntegerDigits ▪ DigitCount ▪ BitAnd ▪ FactorInteger ▪ Prime ▪ PrimePi ▪ EulerPhi ▪ MoebiusMu ▪ DivisorSigma ▪ JacobiSymbol ▪ MultiplicativeOrder ▪ PartitionsP ▪ SquaresR ▪ DirichletL ▪ FunctionInjective ▪ FunctionSign ▪ FunctionSingularities ▪ NormalDistribution ▪ ChiSquareDistribution ▪ PoissonDistribution ▪ RandomInteger ▪ RandomReal ▪ RandomChoice ▪ RandomPrime ▪ SquareWave ▪ TriangleWave ▪ UnitBox ▪ MandelbrotSetMemberQ ▪ JuliaSetIterationCount ▪ CantorStaircase ▪ MathematicalFunctionData ▪ Gamma ▪ Pochhammer ▪ Beta ▪ PolyGamma ▪ LogGamma ▪ Erf ▪ Erfc ▪ ExpIntegralE ▪ ExpIntegralEi ▪ LogIntegral ▪ FresnelS ▪ SinIntegral ▪ HermiteH ▪ LaguerreL ▪ JacobiP ▪ GegenbauerC ▪ ChebyshevT ▪ ChebyshevU ▪ ZernikeR ▪ SphericalHarmonicY ▪ WignerD ▪ BesselJ ▪ BesselY ▪ BesselI ▪ BesselK ▪ AiryAi ▪ AiryAiPrime ▪ SphericalBesselJ ▪ KelvinBer ▪ HankelH1 ▪ StruveH ▪ LegendreP ▪ LegendreQ ▪ SpheroidalQS ▪ Hypergeometric2F1 ▪ HypergeometricPFQ ▪ HypergeometricU ▪ MeijerG ▪ FoxH ▪ AppellF1 ▪ BilateralHypergeometricPFQ ▪ EllipticK ▪ EllipticF ▪ EllipticE ▪ EllipticPi ▪ CarlsonRF ▪ CarlsonRK ▪ JacobiSN ▪ InverseJacobiSN ▪ WeierstrassP ▪ EllipticTheta ▪ DedekindEta ▪ KleinInvariantJ ▪ ModularLambda ▪ SiegelTheta ▪ Zeta ▪ PolyLog ▪ LerchPhi ▪ RiemannSiegelZ ▪ MathieuS ▪ MathieuSPrime ▪ MathieuC ▪ MathieuCharacteristicA ▪ SpheroidalPS ▪ SpheroidalS1 ▪ SpheroidalEigenvalue ▪ HeunG ▪ HeunC ▪ HeunB ▪ HeunD ▪ HeunT ▪ CoulombF ▪ CoulombG ▪ CoulombH1 ▪ CoulombH2 ▪ QFactorial ▪ QPochhammer ▪ QHypergeometricPFQ ▪ MittagLefflerE ▪ ProductLog ▪ InverseErf ▪ InverseGammaRegularized ▪ InverseEllipticNomeQ ▪ InverseWeierstrassP ▪ BesselJZero ▪ ZetaZero ▪ Root ▪ DifferentialRoot ▪ DifferenceRoot ▪ Derivative ▪ FindRoot ▪ Min ▪ Max ▪ RealAbs ▪ Piecewise ▪ Log ▪ Log10 ▪ Log2 ▪ Exp ▪ Power ▪ Sqrt ▪ CubeRoot ▪ Surd ▪ Degree ▪ Sin ▪ Cos ▪ Tan ▪ ArcSin ▪ ArcCos ▪ ArcTan ▪ Sinc ▪ Sinh ▪ Cosh ▪ Tanh ▪ ArcSinh ▪ ArcCosh ▪ ArcTanh ▪ N ▪ FunctionExpand ▪ FullSimplify ▪ Series ▪