Wolfram数学函数Wolfram 语言
的核心内容

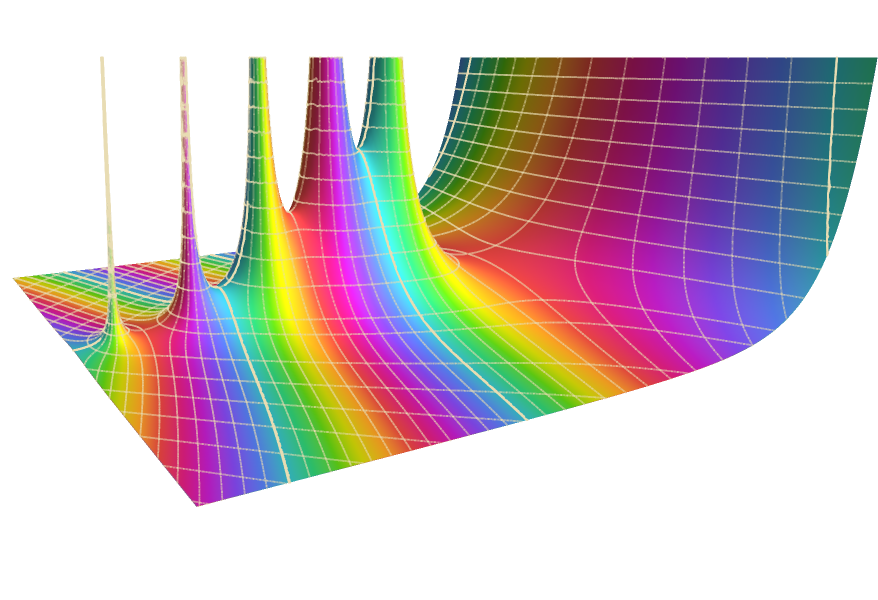
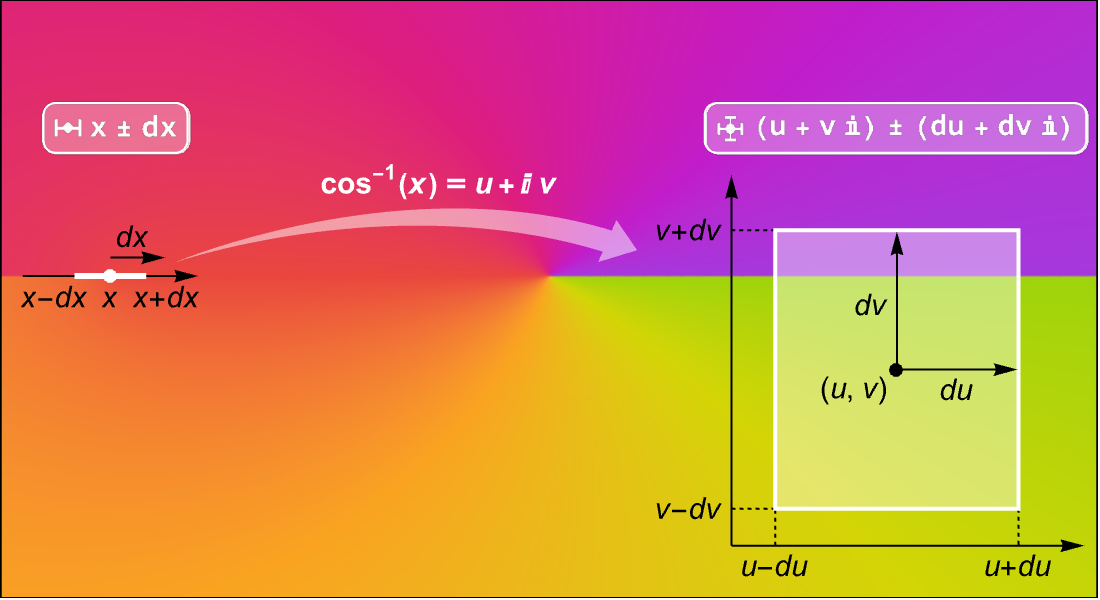
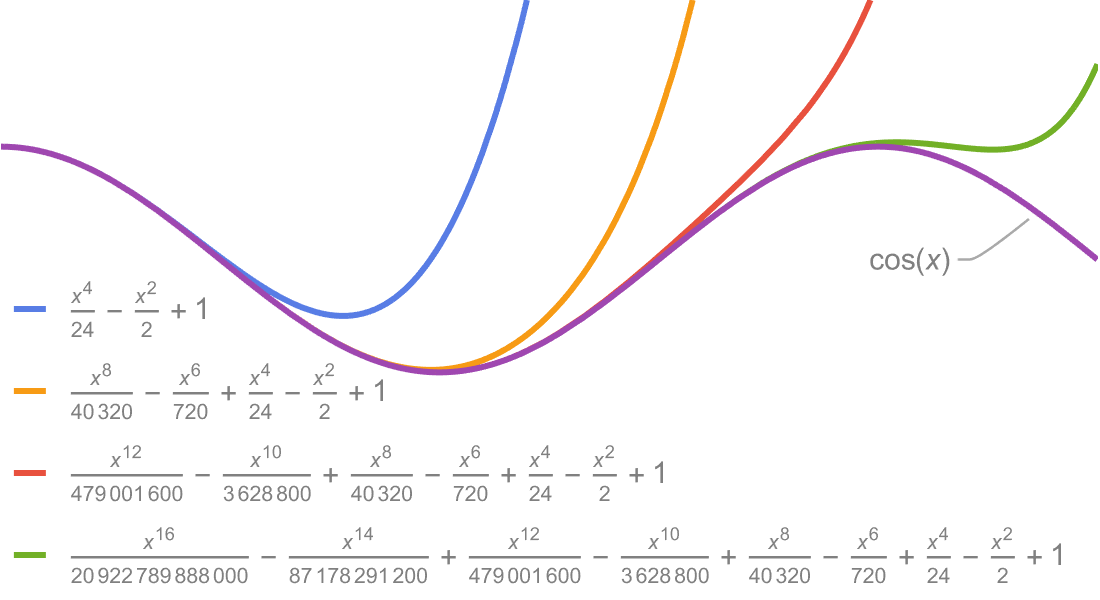
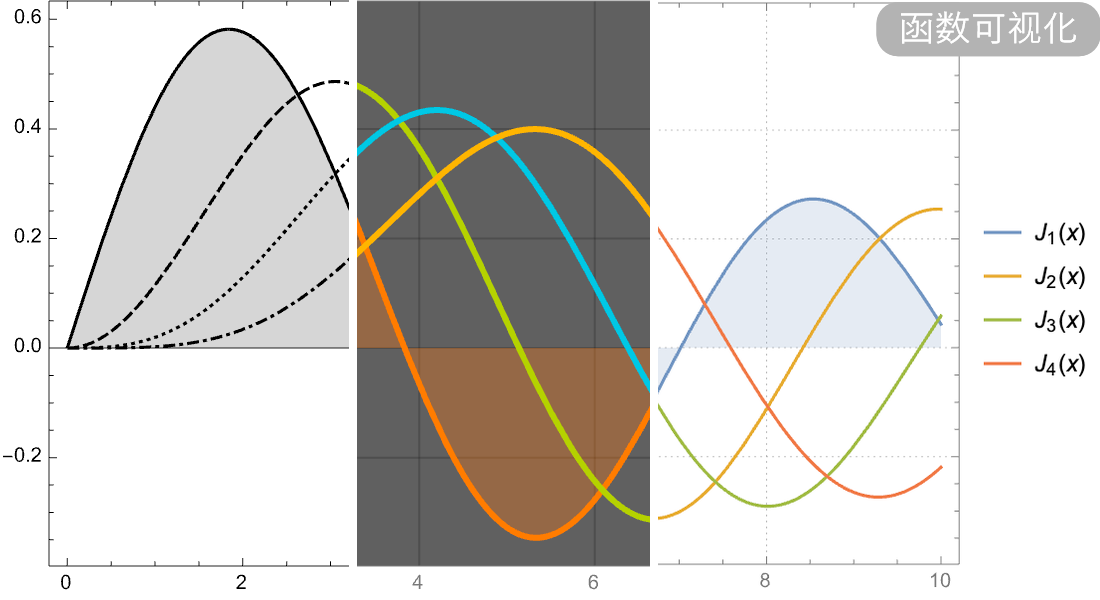
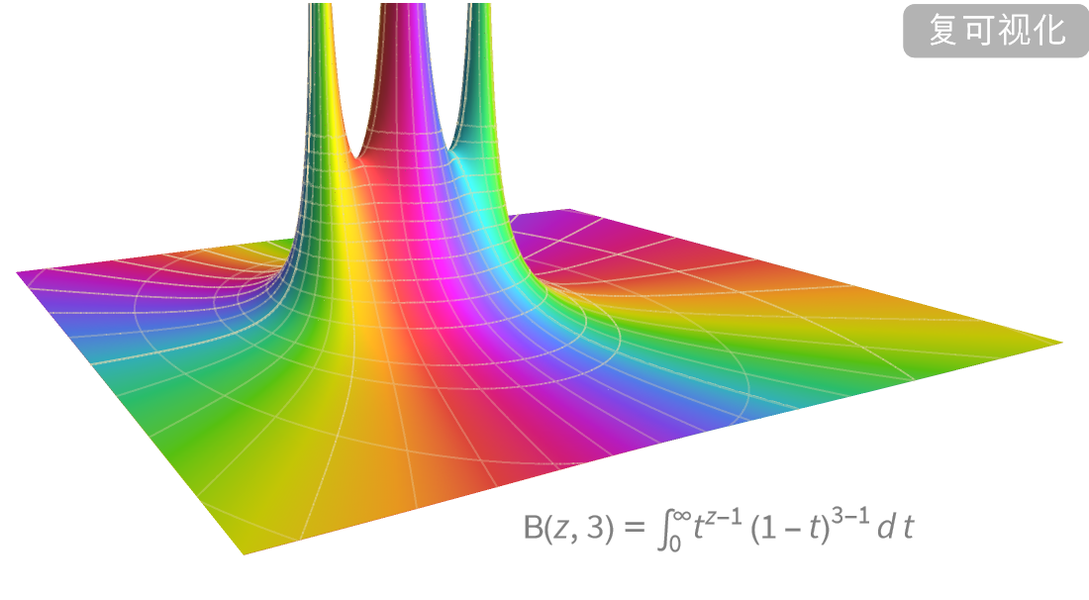
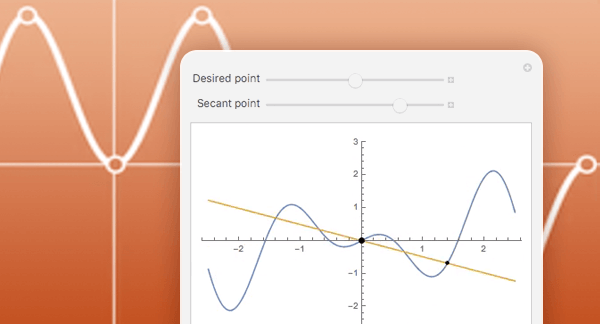
定义、计算与可视化。

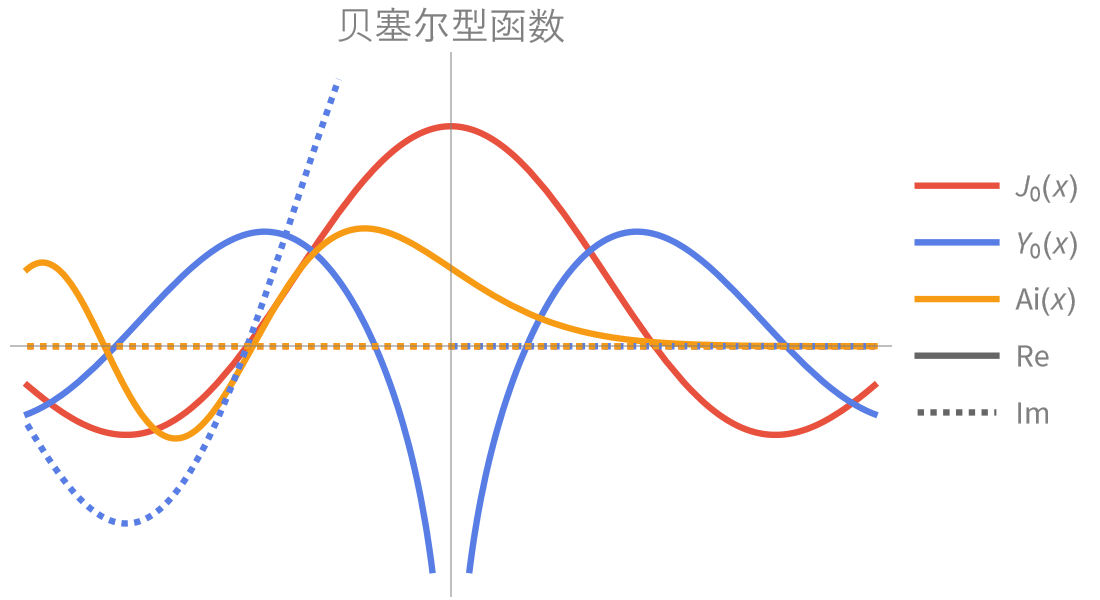
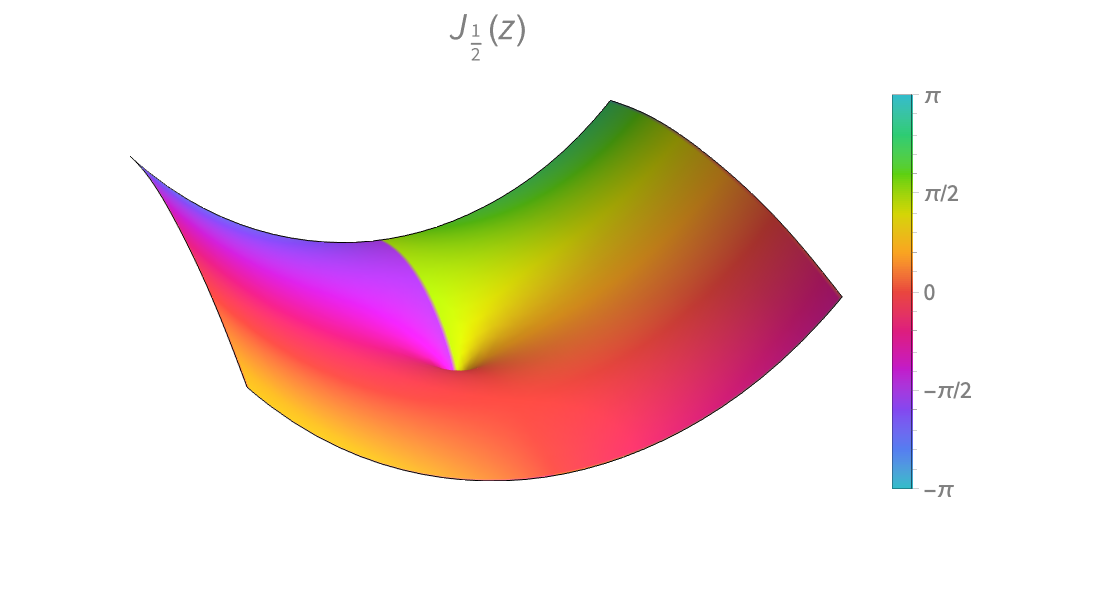
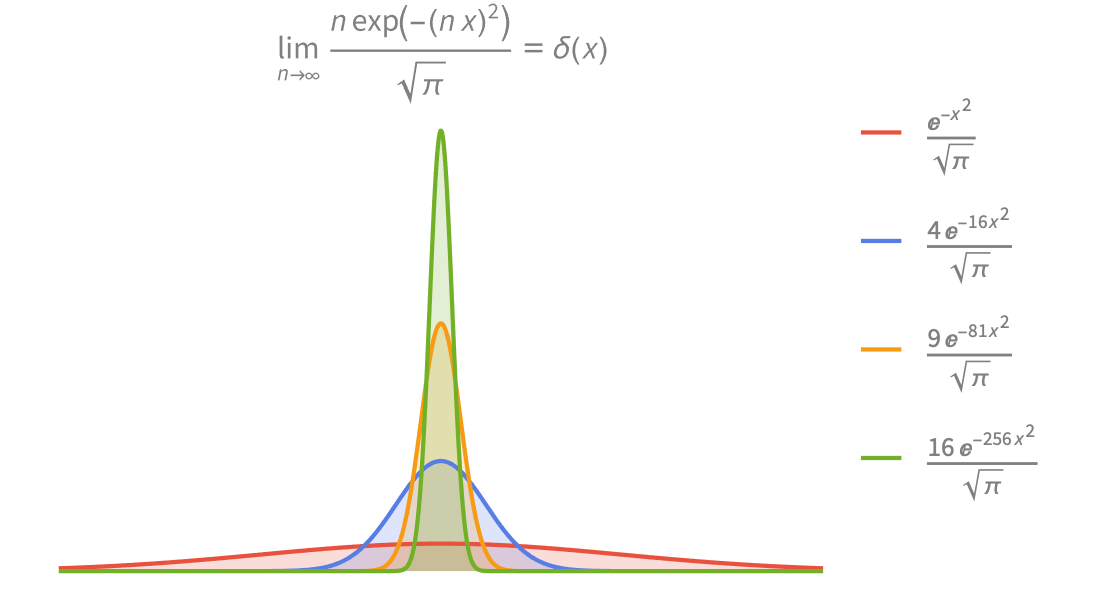
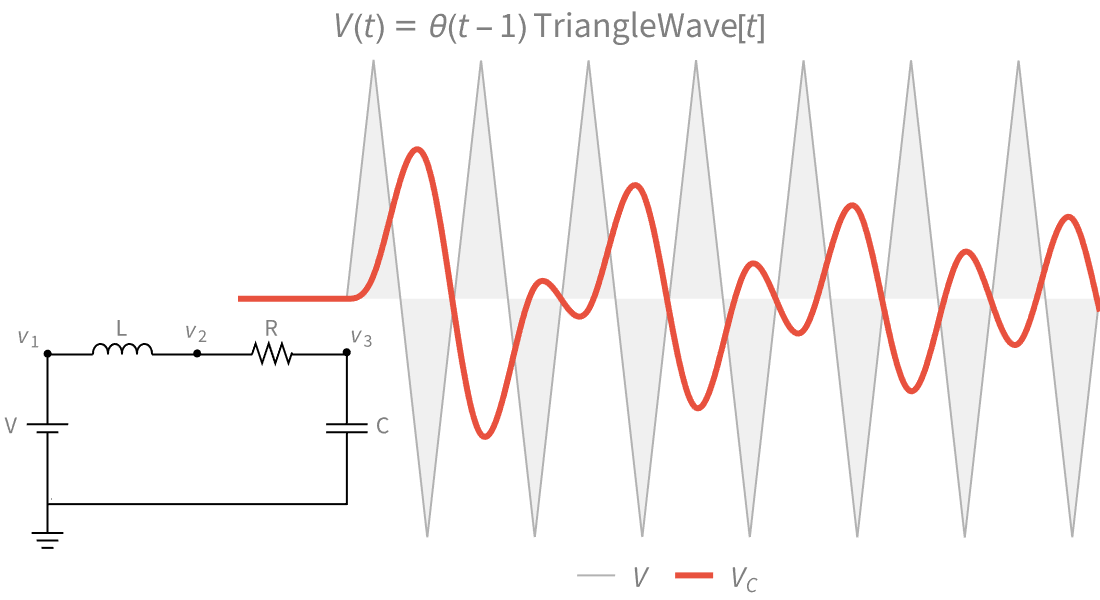
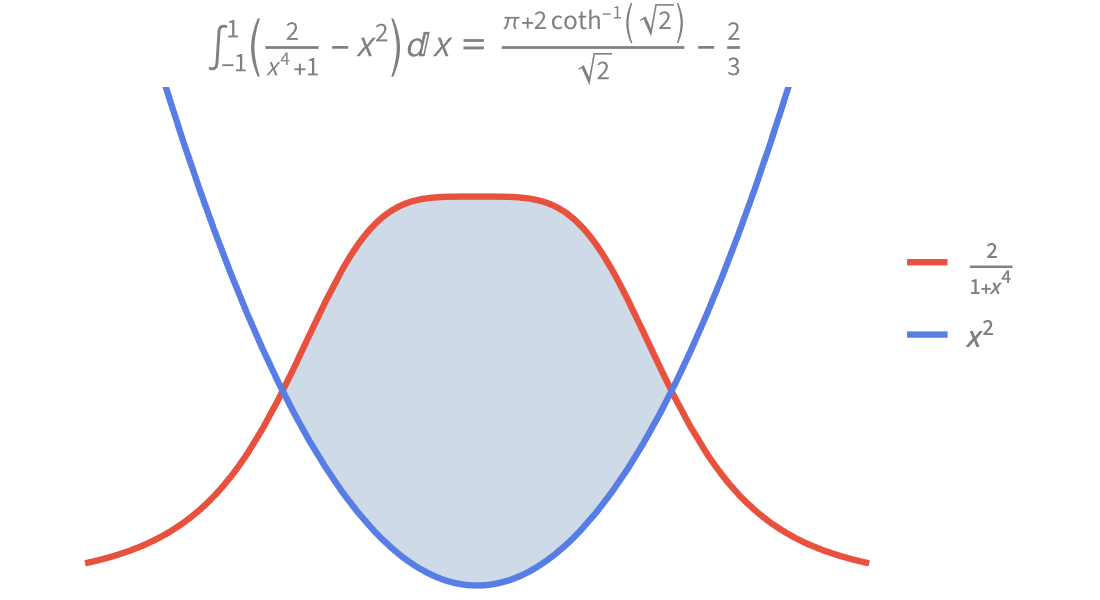
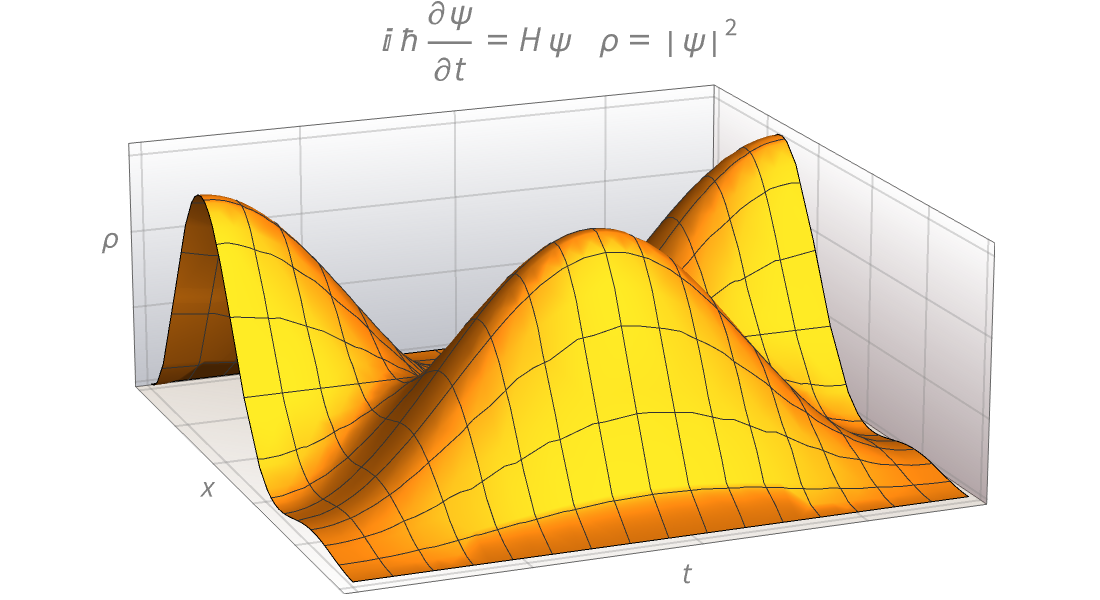
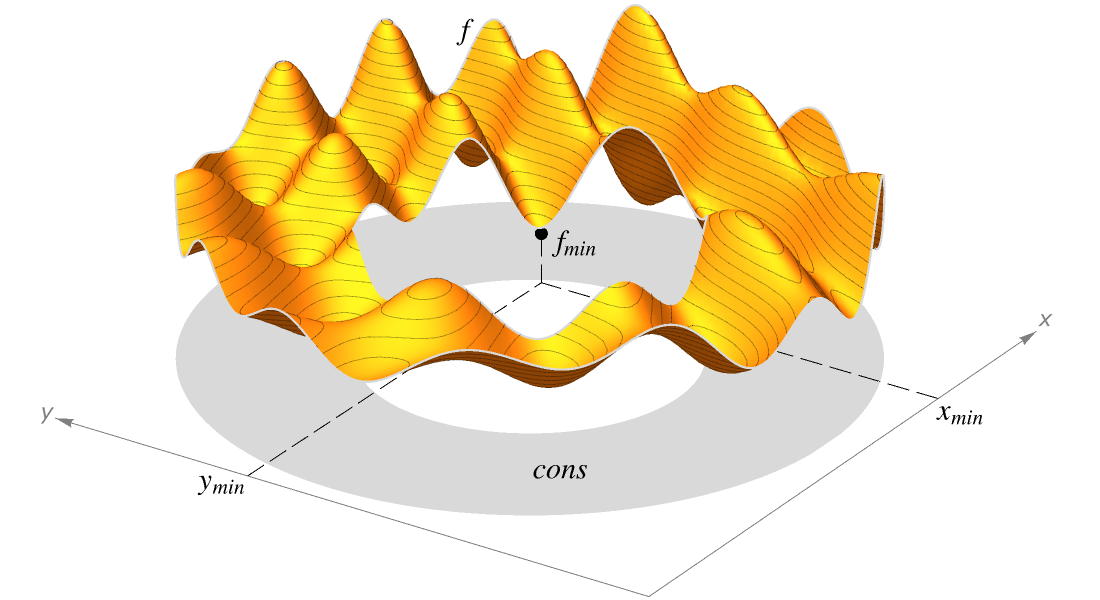
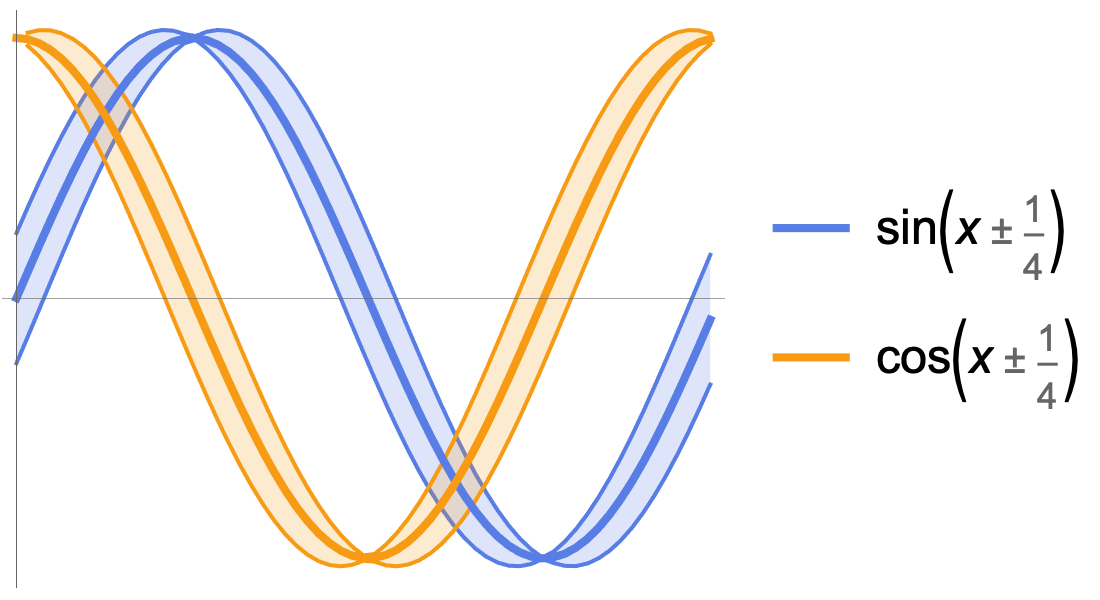
大量数学函数的符号和数值运算、可视化以及渐近展开，我们进行了广泛收录并与 Wolfram 语言的所有领域紧密集成。

开始使用

最完整的汇集

广泛汇集了数百种从初等到高级的特殊函数，并紧密集成到符号和数值求解器中。以任意精度计算数值结果，查找或简化公式。详实、多级的交互式帮助文档让任何人都可以轻松释放他们的潜能。

初等函数

快速、精确的数值和符号计算，适用于科学和工程应用。内置指数函数、三角函数和双曲函数，用于对增长、衰减和振荡行为的组合进行建模。

特殊函数

通过高精度数值或符号级数展开，求解物理、工程、概率和统计问题。

分段函数和广义函数

使用一整套逐点定义的分段函数和广义函数对工程和物理系统进行建模。使用分段函数构建自己的函数。

整数函数

探索含有二项式系数、斐波那契数和调和数以及其他整数函数的数列和级数。使用内置符号求和、递归方程求解和数列识别来解决组合数学、算法理论和其他领域的问题。

函数的性质

快速计算函数的逾 15 个关键数学性质及求和、乘积与组合，以确保多个程序的数学有效性。

符号计算

获得积分、微分方程和许多其他问题的最佳解析解。简化公式并计算精确答案。使用全面的数学函数集，精确而简洁地将问题输入到符号求解器中。

数值计算

以机器精度或指定的任意精度计算任何数学函数的值。在实轴和复平面上使用区间进行严格的边界计算。轻松传播统计不确定性。使用任何所需的函数将问题准确地输入到数值求解器中。

渐近计算

当精确符号运算失败且数值运算不可靠时，计算函数的渐近逼近，以对问题进行符号分析。稳健的级数系统允许将任何解析函数用作输入，广义级数可以通过继续使用所需的数学函数来简洁地表示结果。

可视化

生成用于报告和论文的高质量插图，深入了解数学函数的行为。

Wolfram 数学函数的相关参考资料

Wolfram 数学函数是 Wolfram 语言的一个组成部分。整个系统包含了六千多个内置函数，涵盖了计算领域的方方面面，所有内容被精心集成在一起，相互支持，完美地结合为一个整体。

Pi ▪ E ▪ EulerGamma ▪ I ▪ Re ▪ Im ▪ Conjugate ▪ Arg ▪ Plus ▪ Times ▪ Total ▪ Abs ▪ Round ▪ Floor ▪ Clip ▪ Ramp ▪ Rescale ▪ DiracDelta ▪ HeavisideTheta ▪ DiracComb ▪ Mod ▪ Quotient ▪ Divisible ▪ GCD ▪ Factorial ▪ Binomial ▪ Fibonacci ▪ BernoulliB ▪ StirlingS1 ▪ IntegerDigits ▪ DigitCount ▪ BitAnd ▪ FactorInteger ▪ Prime ▪ PrimePi ▪ EulerPhi ▪ MoebiusMu ▪ DivisorSigma ▪ JacobiSymbol ▪ MultiplicativeOrder ▪ PartitionsP ▪ SquaresR ▪ DirichletL ▪ FunctionInjective ▪ FunctionSign ▪ FunctionSingularities ▪ NormalDistribution ▪ ChiSquareDistribution ▪ PoissonDistribution ▪ RandomInteger ▪ RandomReal ▪ RandomChoice ▪ RandomPrime ▪ SquareWave ▪ TriangleWave ▪ UnitBox ▪ MandelbrotSetMemberQ ▪ JuliaSetIterationCount ▪ CantorStaircase ▪ MathematicalFunctionData ▪ Gamma ▪ Pochhammer ▪ Beta ▪ PolyGamma ▪ LogGamma ▪ Erf ▪ Erfc ▪ ExpIntegralE ▪ ExpIntegralEi ▪ LogIntegral ▪ FresnelS ▪ SinIntegral ▪ HermiteH ▪ LaguerreL ▪ JacobiP ▪ GegenbauerC ▪ ChebyshevT ▪ ChebyshevU ▪ ZernikeR ▪ SphericalHarmonicY ▪ WignerD ▪ BesselJ ▪ BesselY ▪ BesselI ▪ BesselK ▪ AiryAi ▪ AiryAiPrime ▪ SphericalBesselJ ▪ KelvinBer ▪ HankelH1 ▪ StruveH ▪ LegendreP ▪ LegendreQ ▪ SpheroidalQS ▪ Hypergeometric2F1 ▪ HypergeometricPFQ ▪ HypergeometricU ▪ MeijerG ▪ FoxH ▪ AppellF1 ▪ BilateralHypergeometricPFQ ▪ EllipticK ▪ EllipticF ▪ EllipticE ▪ EllipticPi ▪ CarlsonRF ▪ CarlsonRK ▪ JacobiSN ▪ InverseJacobiSN ▪ WeierstrassP ▪ EllipticTheta ▪ DedekindEta ▪ KleinInvariantJ ▪ ModularLambda ▪ SiegelTheta ▪ Zeta ▪ PolyLog ▪ LerchPhi ▪ RiemannSiegelZ ▪ MathieuS ▪ MathieuSPrime ▪ MathieuC ▪ MathieuCharacteristicA ▪ SpheroidalPS ▪ SpheroidalS1 ▪ SpheroidalEigenvalue ▪ HeunG ▪ HeunC ▪ HeunB ▪ HeunD ▪ HeunT ▪ CoulombF ▪ CoulombG ▪ CoulombH1 ▪ CoulombH2 ▪ QFactorial ▪ QPochhammer ▪ QHypergeometricPFQ ▪ MittagLefflerE ▪ ProductLog ▪ InverseErf ▪ InverseGammaRegularized ▪ InverseEllipticNomeQ ▪ InverseWeierstrassP ▪ BesselJZero ▪ ZetaZero ▪ Root ▪ DifferentialRoot ▪ DifferenceRoot ▪ Derivative ▪ FindRoot ▪ Min ▪ Max ▪ RealAbs ▪ Piecewise ▪ Log ▪ Log10 ▪ Log2 ▪ Exp ▪ Power ▪ Sqrt ▪ CubeRoot ▪ Surd ▪ Degree ▪ Sin ▪ Cos ▪ Tan ▪ ArcSin ▪ ArcCos ▪ ArcTan ▪ Sinc ▪ Sinh ▪ Cosh ▪ Tanh ▪ ArcSinh ▪ ArcCosh ▪ ArcTanh ▪ N ▪ FunctionExpand ▪ FullSimplify ▪ Series ▪