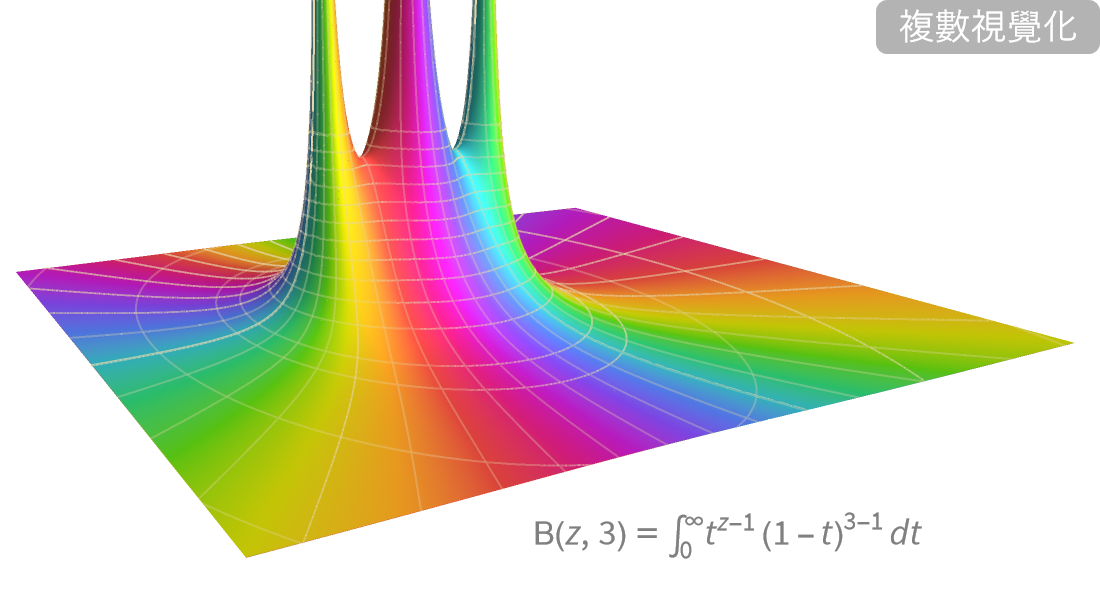
Wolfram數學函數Wolfram 語言
的核心部分
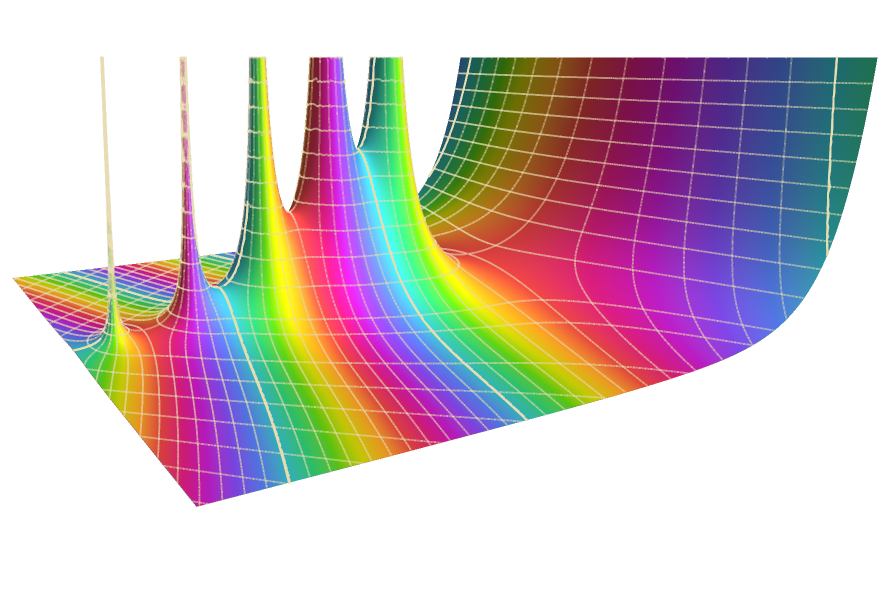
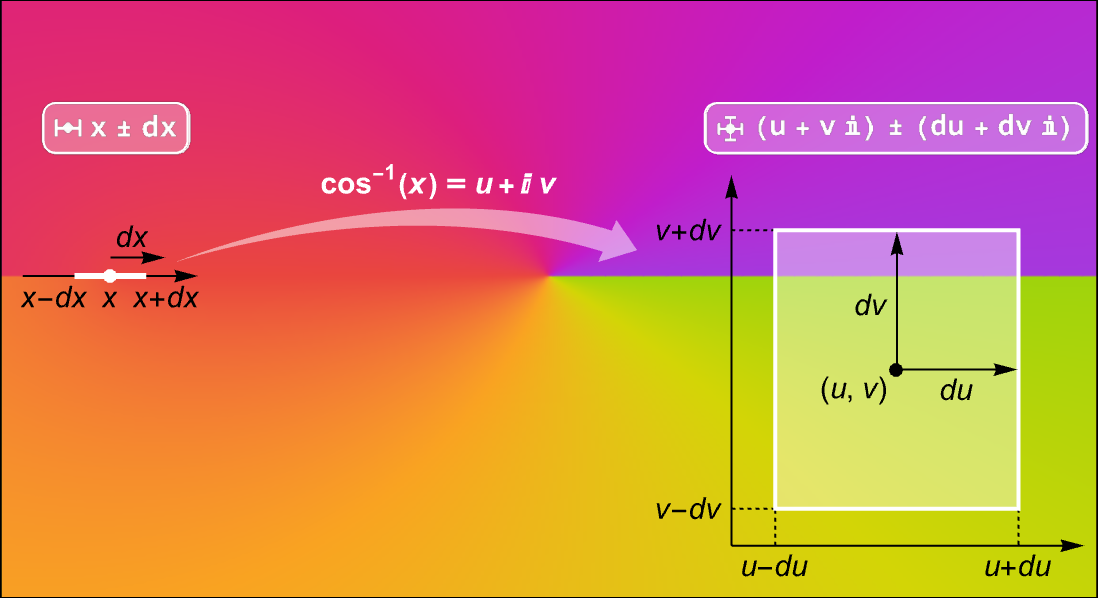
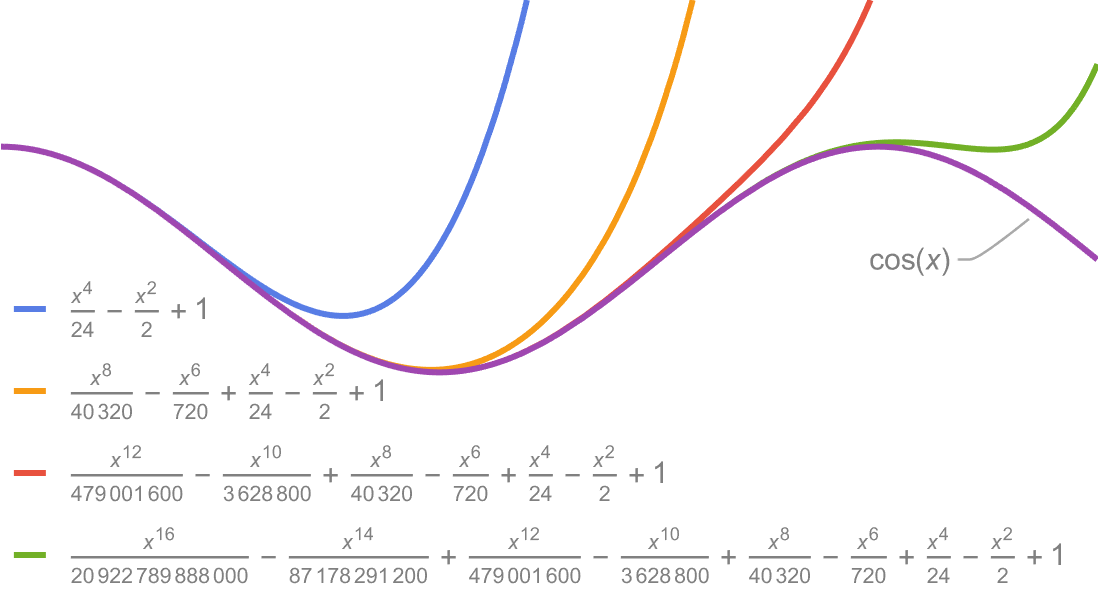
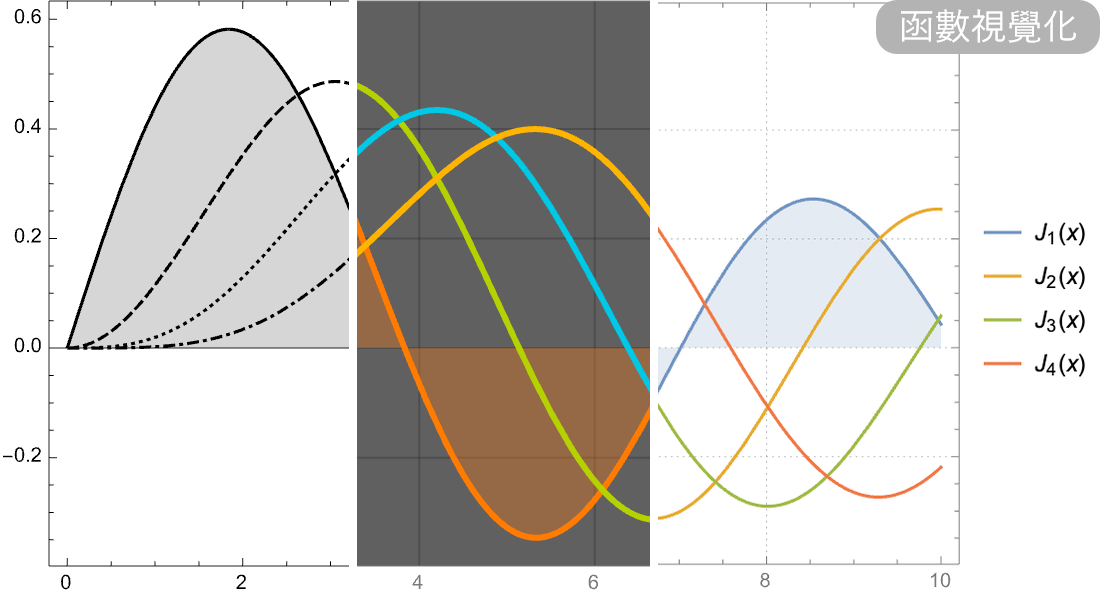
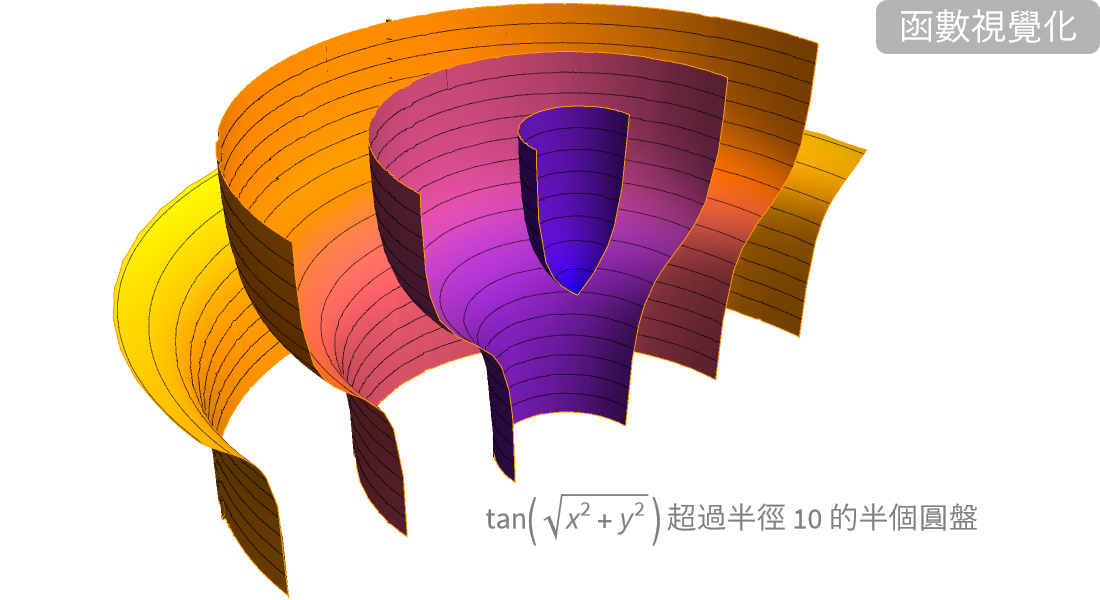
定義，計算和視覺化。
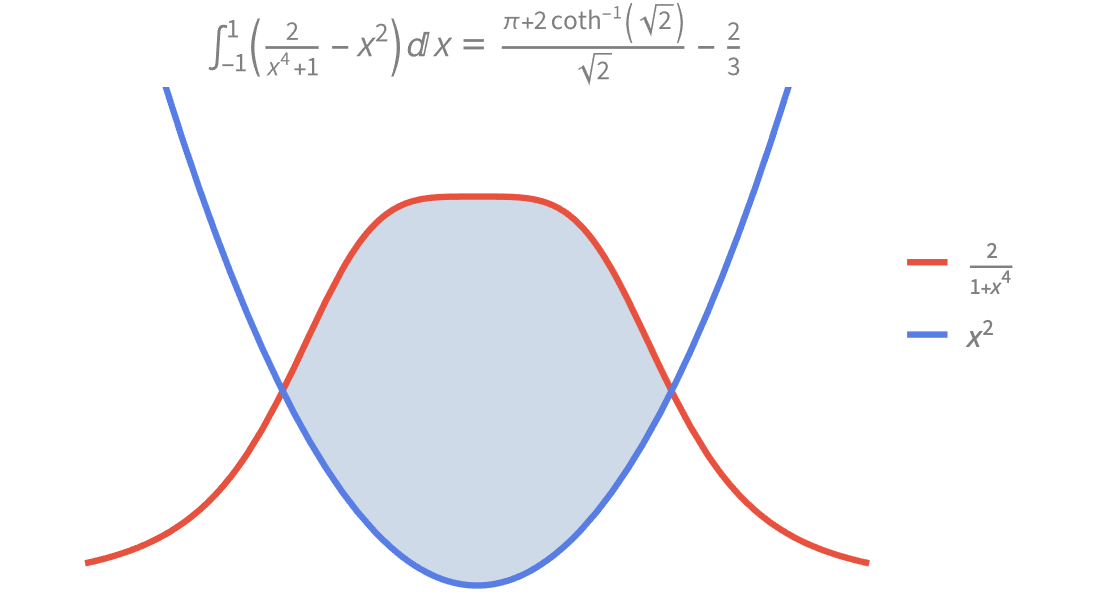
匯集大量數學函數的符號和數值計算、視覺化和漸近展開—廣泛地被記載並與 Wolfram 語言的所有領域緊密整合。
Wolfram 數學函數文檔
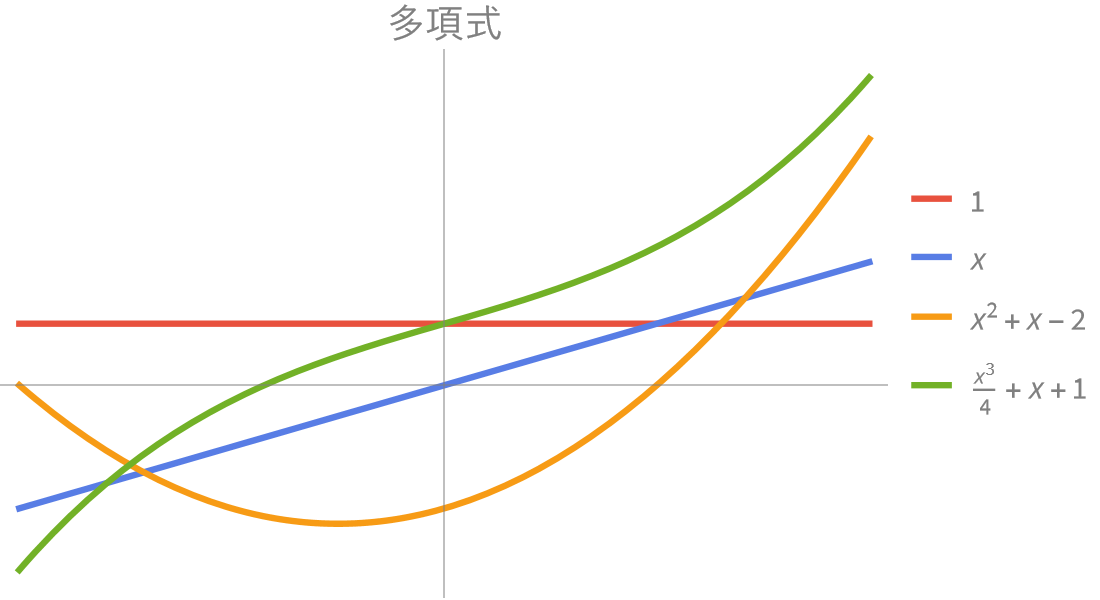
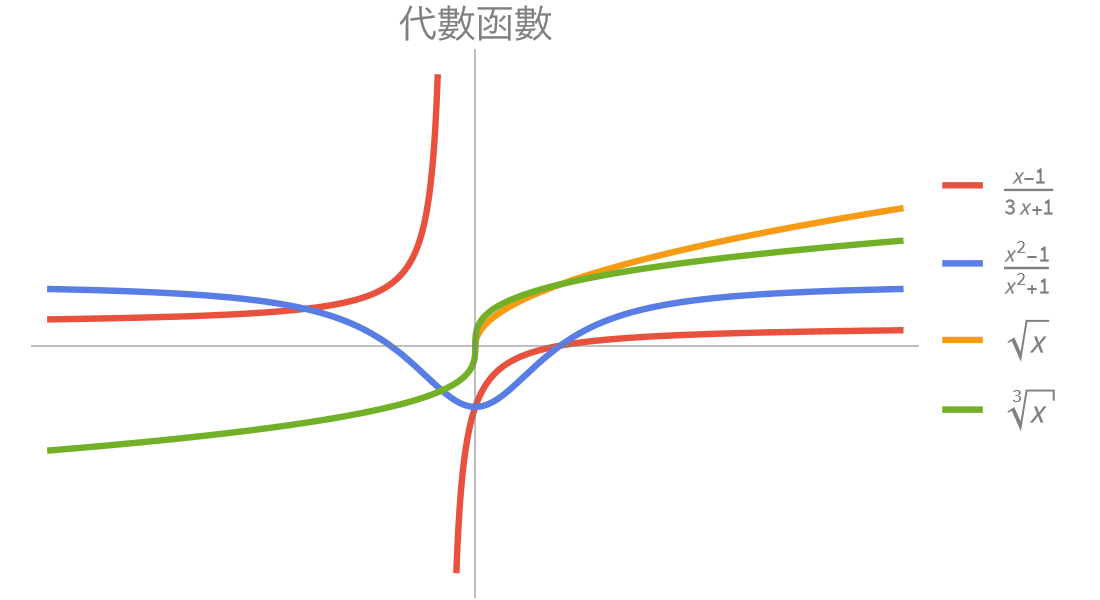
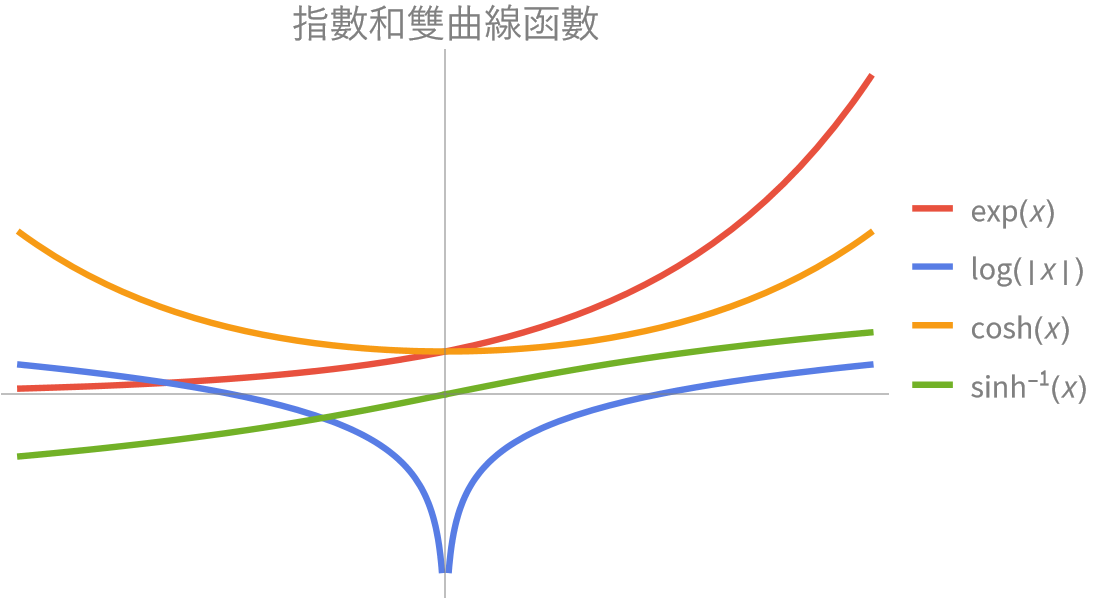
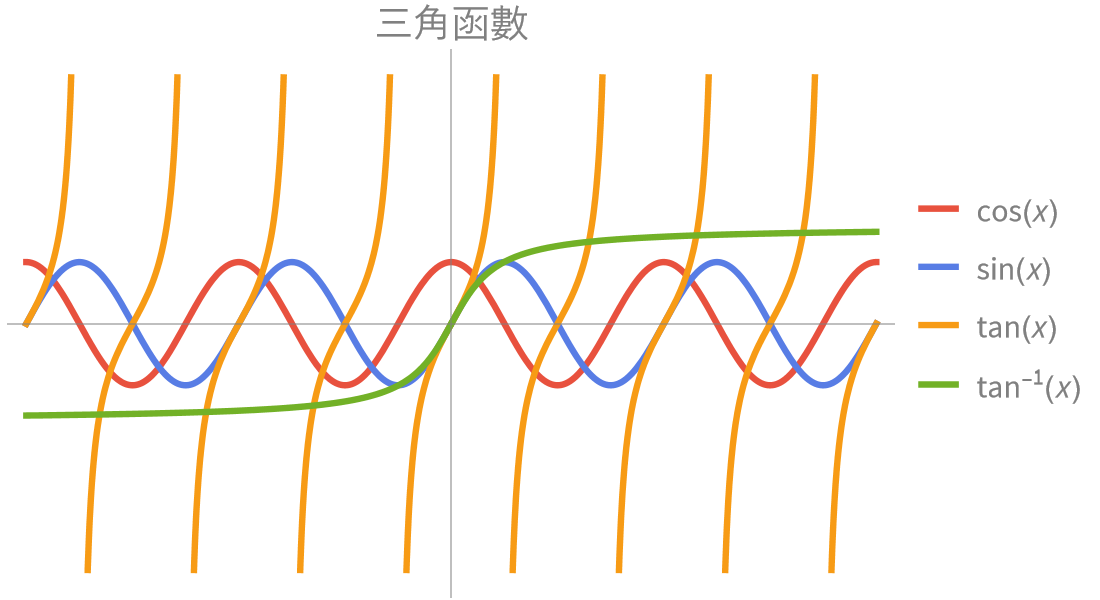
Wolfram 數學函數 是 Wolfram 語言 的部分匯集。完整的系統包含 6,000 多個內建函數，涵蓋所有計算領域 — 都經過精心整合，因此可以完美地將工作結合完成。
完整範圍和文件
Guide
Guide
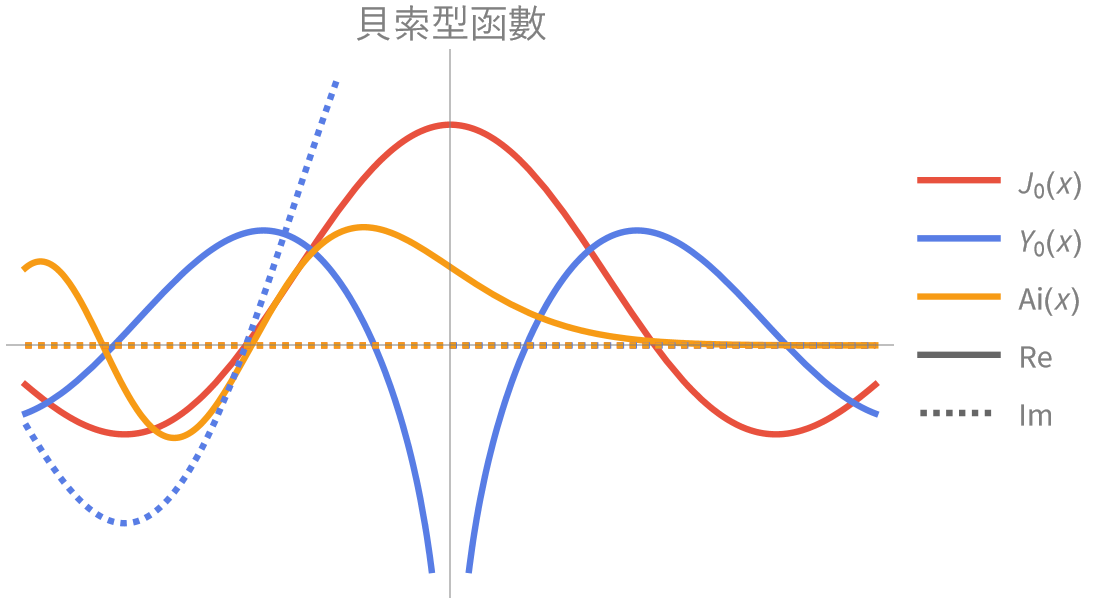
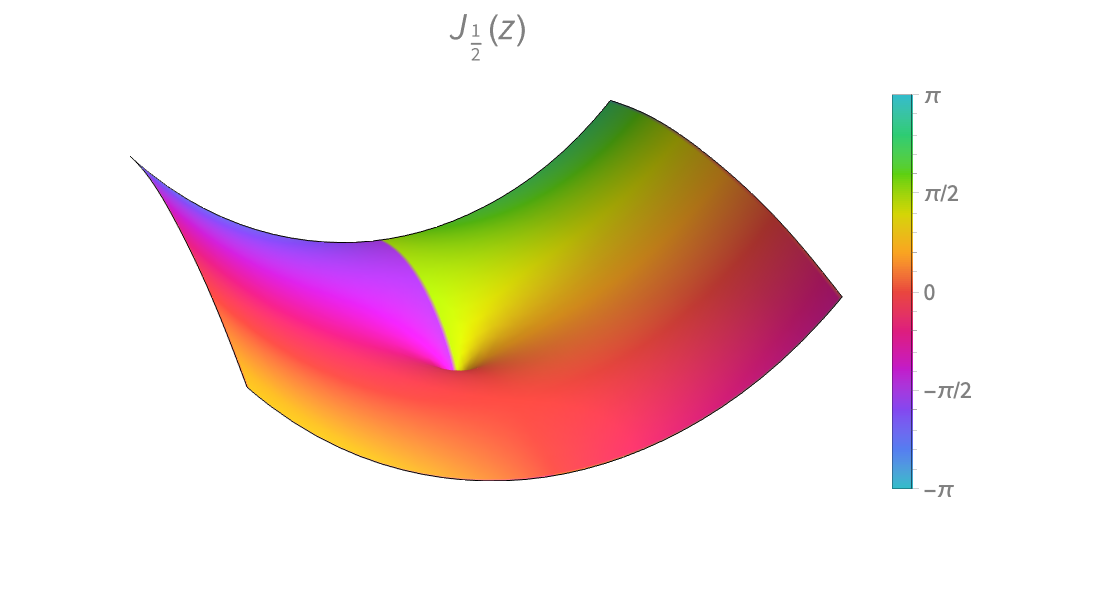
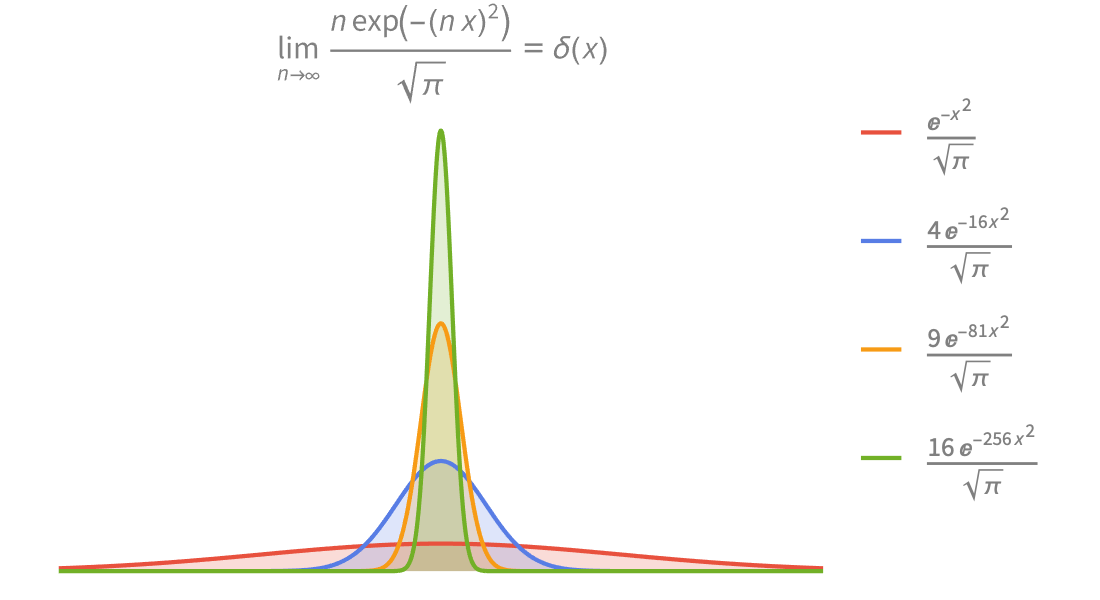
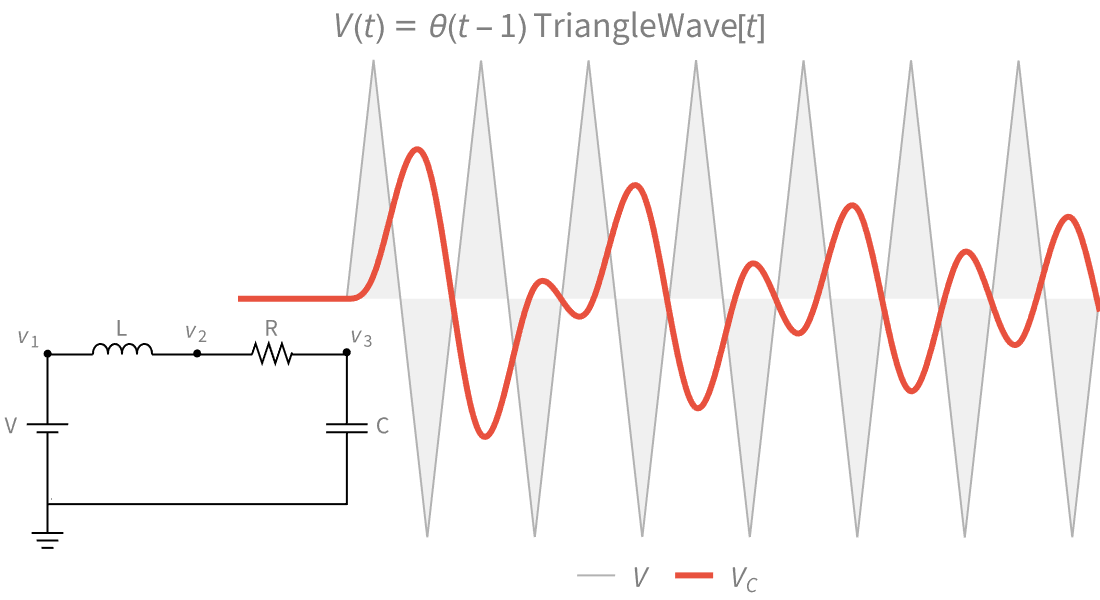
GuidePi ▪ E ▪ EulerGamma ▪ I ▪ Re ▪ Im ▪ Conjugate ▪ Arg ▪ Plus ▪ Times ▪ Total ▪ Abs ▪ Round ▪ Floor ▪ Clip ▪ Ramp ▪ Rescale ▪ DiracDelta ▪ HeavisideTheta ▪ DiracComb ▪ Mod ▪ Quotient ▪ Divisible ▪ GCD ▪ Factorial ▪ Binomial ▪ Fibonacci ▪ BernoulliB ▪ StirlingS1 ▪ IntegerDigits ▪ DigitCount ▪ BitAnd ▪ FactorInteger ▪ Prime ▪ PrimePi ▪ EulerPhi ▪ MoebiusMu ▪ DivisorSigma ▪ JacobiSymbol ▪ MultiplicativeOrder ▪ PartitionsP ▪ SquaresR ▪ DirichletL ▪ FunctionInjective ▪ FunctionSign ▪ FunctionSingularities ▪ NormalDistribution ▪ ChiSquareDistribution ▪ PoissonDistribution ▪ RandomInteger ▪ RandomReal ▪ RandomChoice ▪ RandomPrime ▪ SquareWave ▪ TriangleWave ▪ UnitBox ▪ MandelbrotSetMemberQ ▪ JuliaSetIterationCount ▪ CantorStaircase ▪ MathematicalFunctionData ▪ Gamma ▪ Pochhammer ▪ Beta ▪ PolyGamma ▪ LogGamma ▪ Erf ▪ Erfc ▪ ExpIntegralE ▪ ExpIntegralEi ▪ LogIntegral ▪ FresnelS ▪ SinIntegral ▪ HermiteH ▪ LaguerreL ▪ JacobiP ▪ GegenbauerC ▪ ChebyshevT ▪ ChebyshevU ▪ ZernikeR ▪ SphericalHarmonicY ▪ WignerD ▪ BesselJ ▪ BesselY ▪ BesselI ▪ BesselK ▪ AiryAi ▪ AiryAiPrime ▪ SphericalBesselJ ▪ KelvinBer ▪ HankelH1 ▪ StruveH ▪ LegendreP ▪ LegendreQ ▪ SpheroidalQS ▪ Hypergeometric2F1 ▪ HypergeometricPFQ ▪ HypergeometricU ▪ MeijerG ▪ FoxH ▪ AppellF1 ▪ BilateralHypergeometricPFQ ▪ EllipticK ▪ EllipticF ▪ EllipticE ▪ EllipticPi ▪ CarlsonRF ▪ CarlsonRK ▪ JacobiSN ▪ InverseJacobiSN ▪ WeierstrassP ▪ EllipticTheta ▪ DedekindEta ▪ KleinInvariantJ ▪ ModularLambda ▪ SiegelTheta ▪ Zeta ▪ PolyLog ▪ LerchPhi ▪ RiemannSiegelZ ▪ MathieuS ▪ MathieuSPrime ▪ MathieuC ▪ MathieuCharacteristicA ▪ SpheroidalPS ▪ SpheroidalS1 ▪ SpheroidalEigenvalue ▪ HeunG ▪ HeunC ▪ HeunB ▪ HeunD ▪ HeunT ▪ CoulombF ▪ CoulombG ▪ CoulombH1 ▪ CoulombH2 ▪ QFactorial ▪ QPochhammer ▪ QHypergeometricPFQ ▪ MittagLefflerE ▪ ProductLog ▪ InverseErf ▪ InverseGammaRegularized ▪ InverseEllipticNomeQ ▪ InverseWeierstrassP ▪ BesselJZero ▪ ZetaZero ▪ Root ▪ DifferentialRoot ▪ DifferenceRoot ▪ Derivative ▪ FindRoot ▪ Min ▪ Max ▪ RealAbs ▪ Piecewise ▪ Log ▪ Log10 ▪ Log2 ▪ Exp ▪ Power ▪ Sqrt ▪ CubeRoot ▪ Surd ▪ Degree ▪ Sin ▪ Cos ▪ Tan ▪ ArcSin ▪ ArcCos ▪ ArcTan ▪ Sinc ▪ Sinh ▪ Cosh ▪ Tanh ▪ ArcSinh ▪ ArcCosh ▪ ArcTanh ▪ N ▪ FunctionExpand ▪ FullSimplify ▪ Series ▪
開始使用 Wolfram 數學函數
經由 Wolfram|One 或 Mathematica 使用 Wolfram 語言
