WolframOptimierungEin Kernbestandteil der
Wolfram Language
Entwürfe modellieren, lösen und analysieren.
Wolfram Optimization bietet ein umfassendes Set von Werkzeugen, um den besten Entwurf zu finden oder die beste Entscheidung unter Berücksichtigung gegebener Nebenbedingungen zu treffen – mit vollständig integriertem hochautomatisiertem maschinellem Lernen, Statistik, sofort berechenbaren integrierten Daten und mehr.
Optimierungsprobleme modellieren
Modellieren Sie Zielfunktionen und Nebenbedingungen mit Hilfe von mathematischen Funktionen, Ungleichungen und Teilmengen. Definieren Sie kompakte High-Level-Modelle auf natürliche Weise mit Vektorvariablen, Vektorungleichungen und geometrischen Regionen. Erstellen Sie wiederverwendbare Modelle, die Sie programmatisch aus Daten, Diagrammen und anderen Objekten konstruieren.
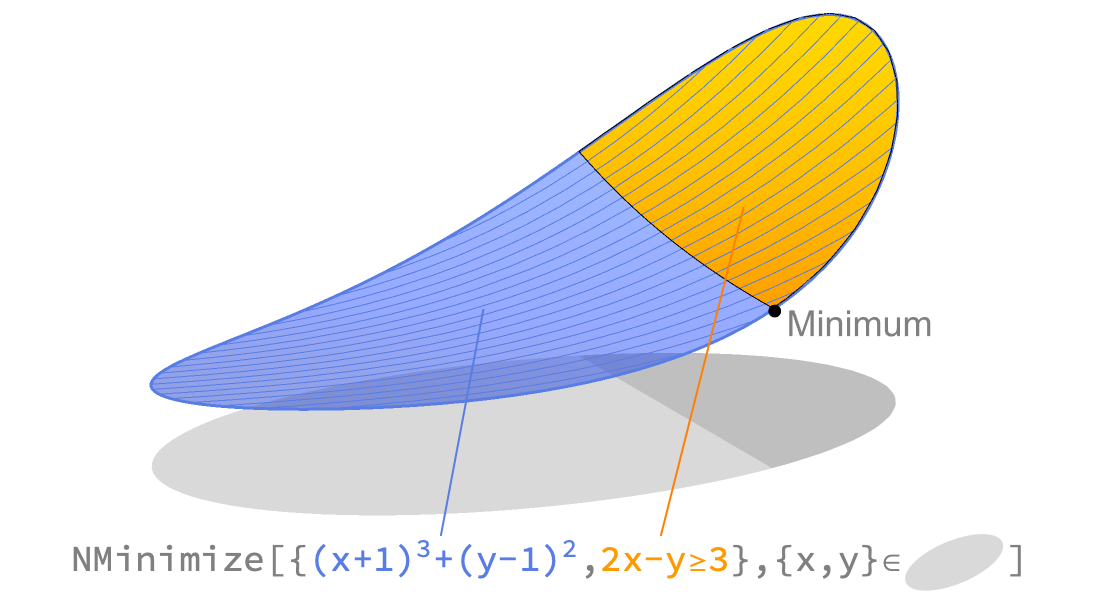
Lineare & konvexe Optimierung
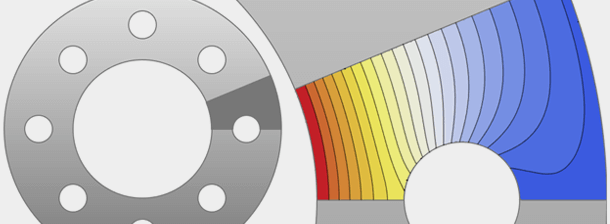
Lösen Sie große konvexe Optimierungsprobleme mit globalen, schnellen und zuverlässigen Methoden. Die konvexe Optimierung umfasst wichtige Klassen wie lineare und quadratische Optimierung, SOCPs, semidefinite und konische Optimierung.
Lokale Optimierung
Finden Sie ein lokales Optimum für uneingeschränkte oder eingeschränkte Optimierungsprobleme. Lokale Methoden sind schnell und skalierbar und ausreichend, oder werden zur Entwicklung komplexerer Methoden verwendet. Lösen Sie Optimierungsprobleme effizient dank automatisch ausgewählter Methoden, vom Quasi-Newton-Verfahren bis zum Innere-Punkte-Verfahren, der Berechnung von Ableitungen und Kompilierung.
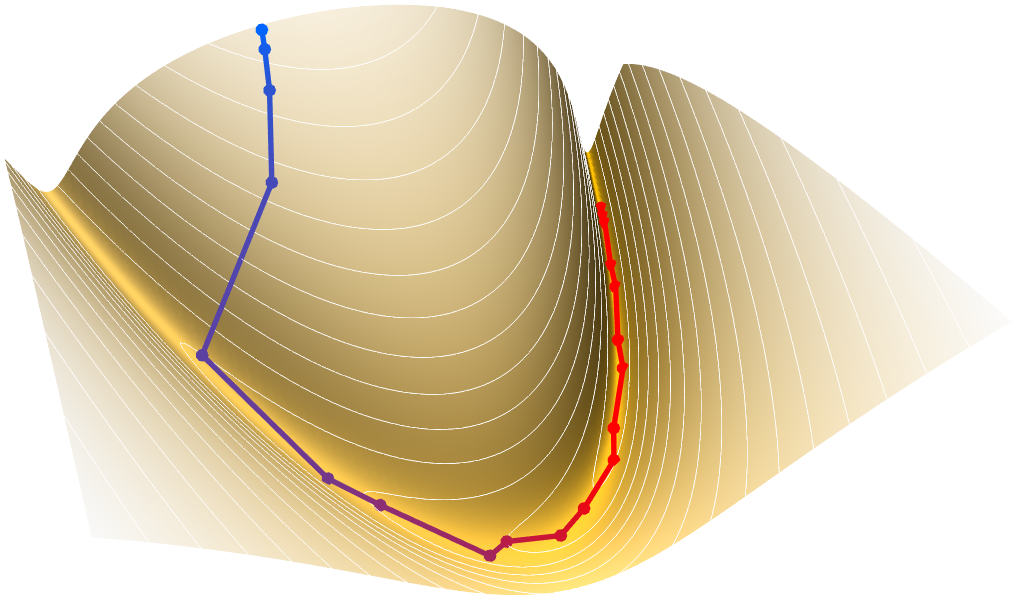
Globale Optimierung
Suchen Sie nach den bestmöglichen Variablen für eine Zielfunktion mit Nebenbedingungen. Der zusätzliche Aufwand, der für die Suche nach einem globalen Optimum erforderlich ist, lohnt sich oft aus finanziellen, Sicherheits- oder Effizienzgründen. Eine Vielzahl von Methoden steht Ihnen zur Verfügung, von deterministischen Algorithmus-Erweiterungen über konvexe Optimierung bis hin zu stochastischen evolutionären Algorithmen.
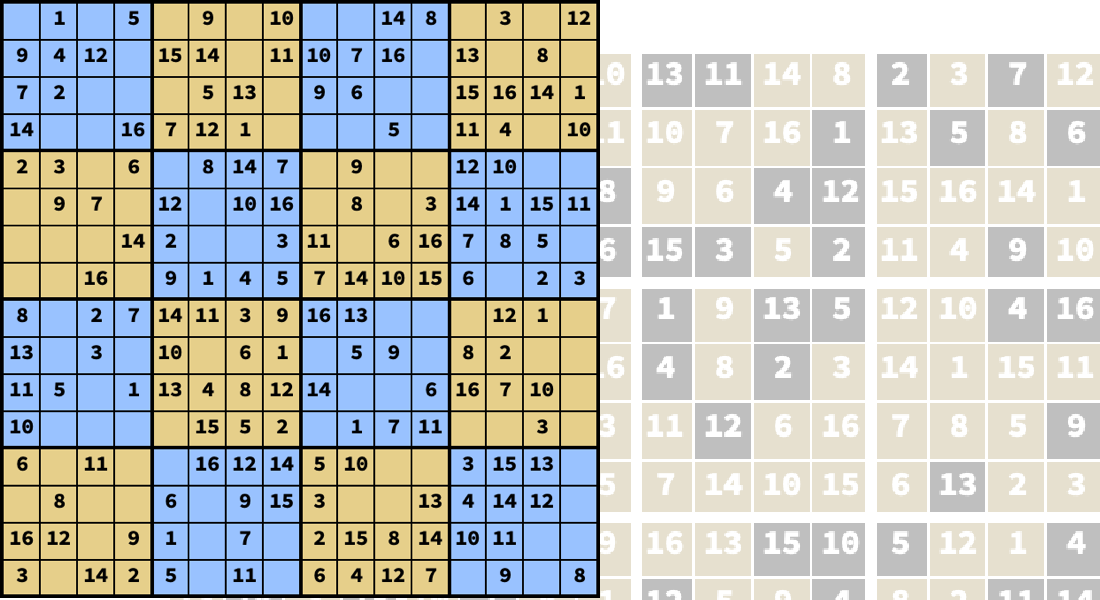
Gemischt-ganzzahlige Optimierung
Lösen Sie konvexe Optimierungsprobleme, bei denen einige der Entscheidungsvariablen nur diskrete oder ganzzahlige Werte haben können. Diskrete Variablen treten häufig bei Zuweisungs-, Planungs- und Streckenoptimierungsproblemen auf. Setzen Sie Branch-and-Bound-Methoden, Schnittebenenverfahren und äußere Approximationsverfahren zur effizienten Lösung gemischt-ganzzahliger Optimierungsprobleme ein.
Parametrische Optimierung
Lösen Sie Familien von Optimierungsproblemen durch die Verwendung von Parametern in Zielfunktionen und Nebenbedingungen. Suchen Sie effizient nach mehreren Lösungen (Parameter-Sweeps), sicheren Lösungen für alle Werte (robuste Optimierung), erwarteten Lösungen für zufällige Werte (stochastische Optimierung) oder nach der Sensitivität gegenüber Änderungen an den Eingangsvariablen (parametrische Empfindlichkeit).
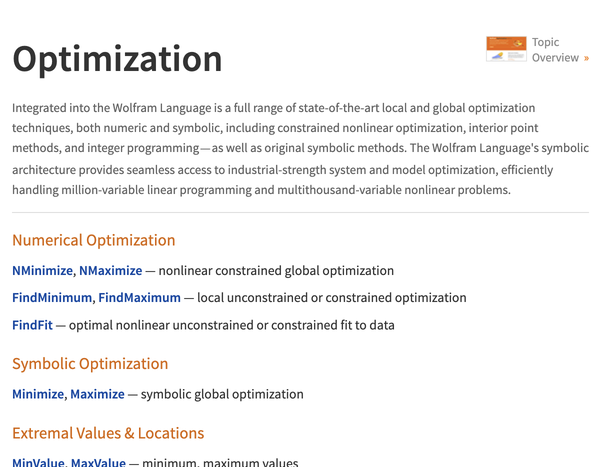
Symbolische Optimierung
Ermitteln Sie Formeln für exakte globale Lösungen von Optimierungsproblemen. Lösungen in geschlossener Form sind verifiziert, wiederverwendbar und mit anderen Formeln kombinierbar. Verwenden Sie dieselbe Modellierungssprache mit exakten symbolischen oder approximativen numerischen Methoden.
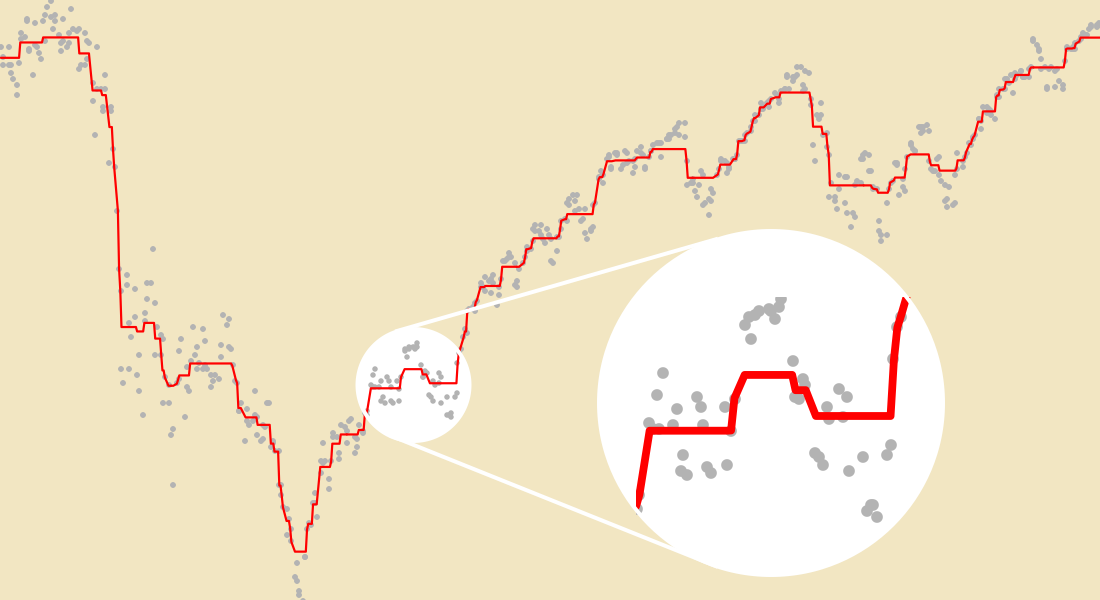
Optimale Anpassung
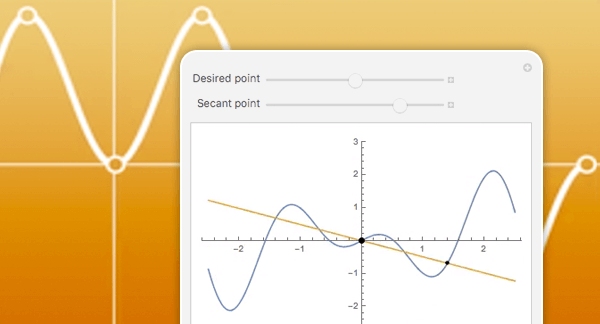
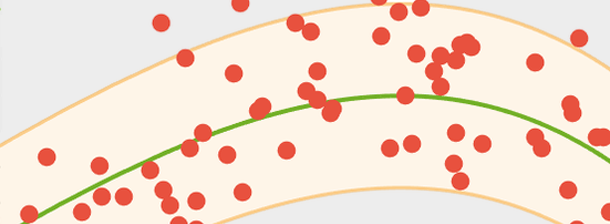
Finden Sie die Modellparameter, die am besten zu Ihrem Datensatz passen. Die Modellanpassung ist die Brücke zwischen Modellen und Daten und ermöglicht die einfache Ableitung anderer Werte. Verwenden Sie lineare und nichtlineare Anpassungsalgorithmen, die Ziele wie kleinste Quadrate, kleinste absolute Abweichung, LASSO und Ridge-Regression verwenden.
Optimierung für spezielle Zwecke
Modellieren und lösen Sie wichtige Optimierungsaufgaben auf einfache Weise mit speziellen Funktionen. Nutzen Sie intuitive Schnittstellen, um das Training künstlicher neuronaler Netze, das Problem des Handelsreisenden, das Rucksackproblem und andere spezielle Optimierungsprobleme zu lösen.
Optimierungsmuster
Nutzen Sie ganz unkompliziert die Software von Gurobi, MOSEK und FICO Xpress. Für die Optimierung mit großen und gemischt-ganzzahligen Daten können Ihnen diese erstklassigen Solver den nötigen Vorsprung liefern. Je nach bestehender Lizenz bieten Sie Ihnen auch vielfältige automatische Optimierungsmethoden.
Dokumentation für Wolfram Optimierung
Wolfram Optimierung ist integrierter Bestandteil der Wolfram Language. Das vollständige System enthält über 6.000 eingebaute Funktionen, die alle Bereiche des Rechnens abdecken—alle sorgfältig integriert, damit sie perfekt zusammenarbeiten.
Vollständiger Umfang & Dokumentation
Guide
Guide
GuideEinführungskurse
Erste Schritte mit Wolfram Optimierung
Nutzen Sie die Wolfram Language über Wolfram|One oder Mathematica
