Wolfram최적화WOLFRAM 언어
의 핵심 부분

설계의 모델링, 해결 및 분석.

Wolfram의 최적화는 최적의 설계를 찾거나 제약 조건 내에서 최상의 결정을 내리는 도구의 포괄적 세트를 제공합니다. 이 도구는 고도로 자동화된 기계 학습 및 통계 기능 및 현장에서 계산 가능한 내장 데이터 등과 완벽하게 통합됩니다.

사용 시작하기

최적화 모델링

수학 함수, 부등식, 포함 관계를 목적 함수와 제약 조건을 사용하여 모델링합니다. 컴팩트하고 높은 수준의 모델을 벡터 변수, 벡터 부등식 및 기하학적 영역으로 자연스러운 형태로 정의합니다. 데이터, 그래프 및 기타 객체에서 프로그램을 사용하여 재사용 가능한 모델을 구축합니다.

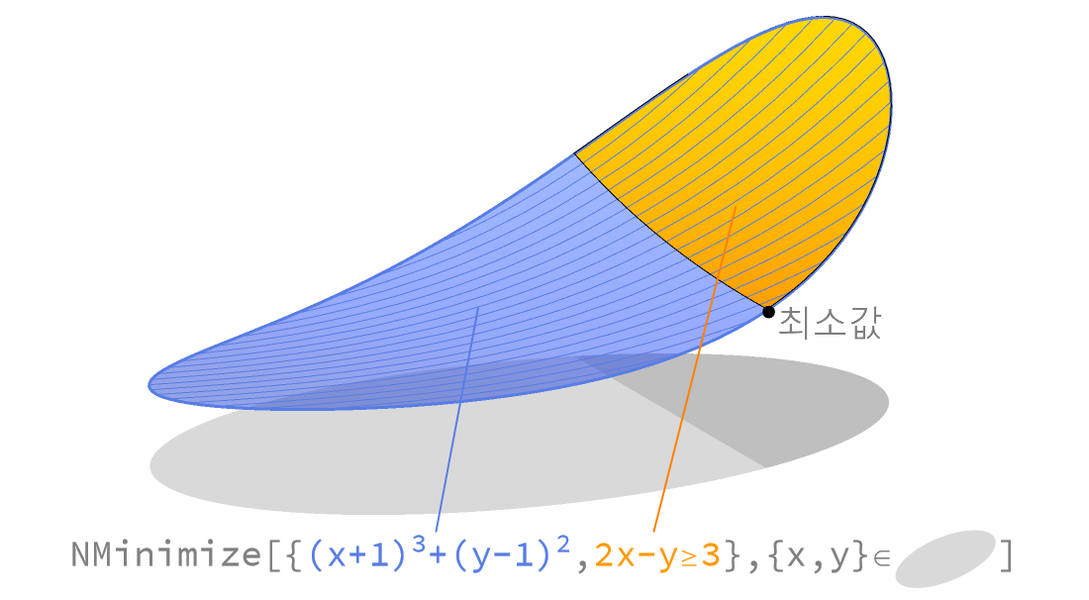
선형 최적화 및 볼록 최적화

대규모 볼록 최적화 문제를 전역적이며 빠르고 신뢰할 수 있는 방법으로 해결합니다. 볼록 최적화에는 선형 최적화, 2차 최적화, 2차 피라미드 최적화, 반정치 최적화, 피라미드 최적화 등의 중요한 클래스가 포함됩니다.

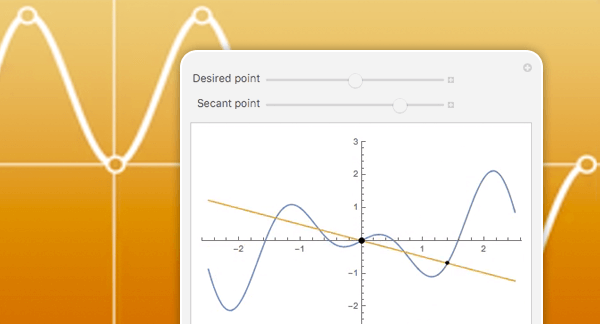
국소 최적화

제약 조건이 있거나 제약 조건이 없는 최적화 문제에 대한 로컬 최적값을 찾습니다. 국소적 방법은 빠르고 확장 가능하며, 그것만으로 충분할 수 있으며 종종 더욱 고급 방법을 만드는 데 사용됩니다. 의사 뉴턴법, 내점법, 도함수의 계산이나 효율화를 위한 컴파일 등으로부터 자동 선택된 메소드를 사용해 해를 구합니다.

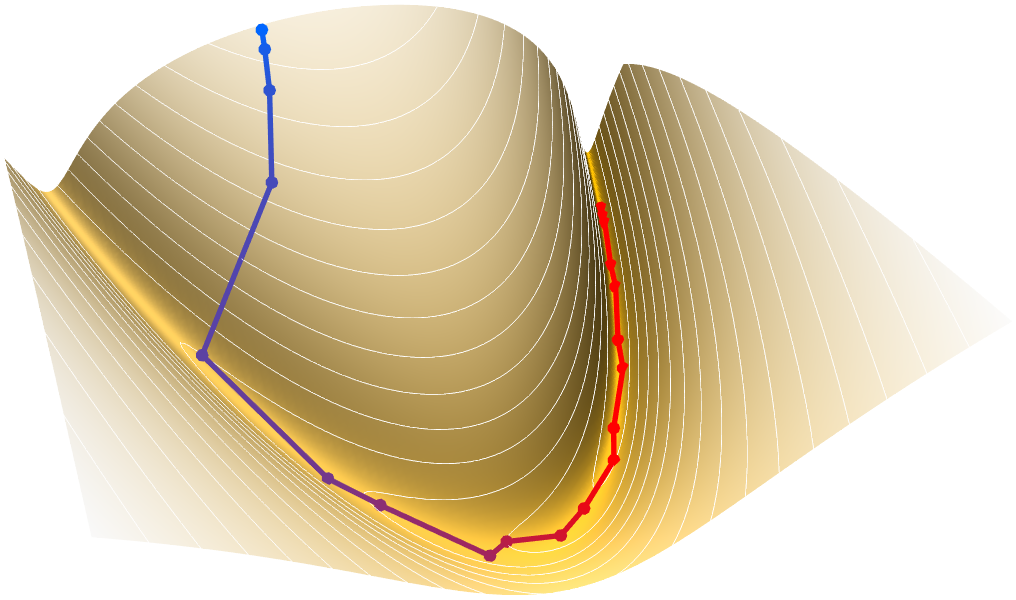
전역적 최적화

목적 함수에 대한 최적값을 제약 조건 내에서 구합니다. 전역적 최적값을 구하는 데는 여분의 노력이 필요하지만, 이 노력은, 많은 경우, 경제, 안전, 효율 등의 이유로 정도의 차이가 있습니다. 결정론적 확장, 볼록 최적화, 확률 론적 진화 등 다양한 방법을 사용할 수 있습니다.

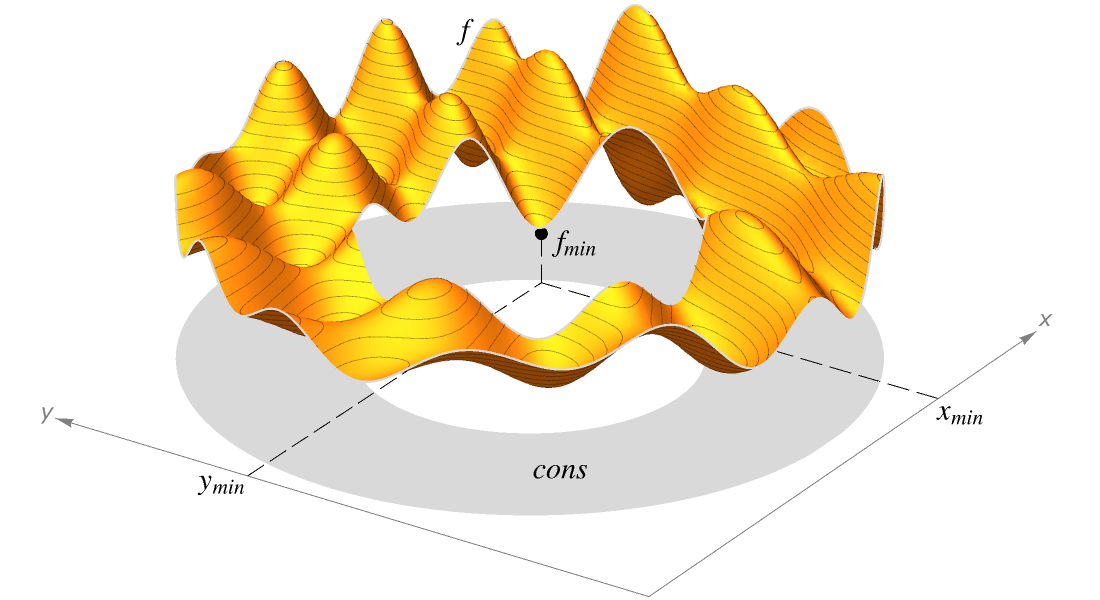
혼합 정수 최적화

결정 변수 중 일부가 이산값 또는 정수값만 가질 수 있는 볼록 최적화 문제를 해결합니다. 이산 변수는 할당, 스케줄링, 경로 선택 등의 문제에서 자주 볼 수 있습니다. 분기 한정법, 절제 평면법, 외측 근사법 등을 사용하여 혼합 정수 문제를 효율적으로 해결합니다.

매개변수 최적화

목적 함수와 제약 조건에서 매개변수를 사용하여 일련의 최적화 문제를 해결합니다. 많은 해를 효율적(파라미터 감도)으로 구하거나, 모든 값에 대해 안전한 해(견고한 최적화), 난수값에 대해 기대되는 해(확률적 최적화), 값의 변화에 대한 감도(파라메트릭 감도)를 요구합니다.

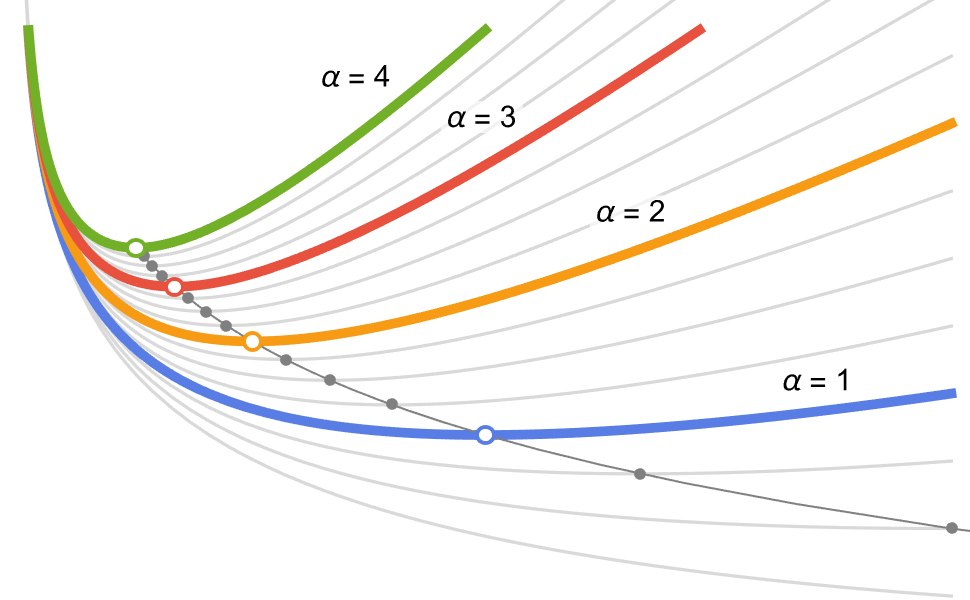
기호 최적화

최적화 문제에 대한 엄격한 전역 해에 대한 공식을 얻습니다. 닫힌 형태의 해는 검증되고 재사용 가능하며 다른 공식과 결합될 수 있습니다. 엄격한 기호 방법과 근사값 방법에 동일한 모델링 언어를 사용할 수 있습니다.

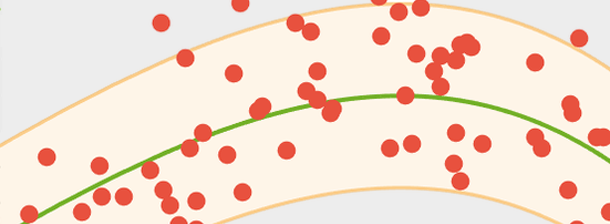
최적의 피팅

데이터 점의 집합을 최적으로 맞추는 모델 매개변수를 찾습니다. 모델 피팅은 모델과 데이터를 연관시켜 다른 값의 추측을 용이하게 합니다. 최소 제곱법, 최소 절대 편차법, LASSO법, 리지 회귀법 등의 목적 함수를 이용하는 선형 및 비선형 피팅 알고리즘을 사용합니다.

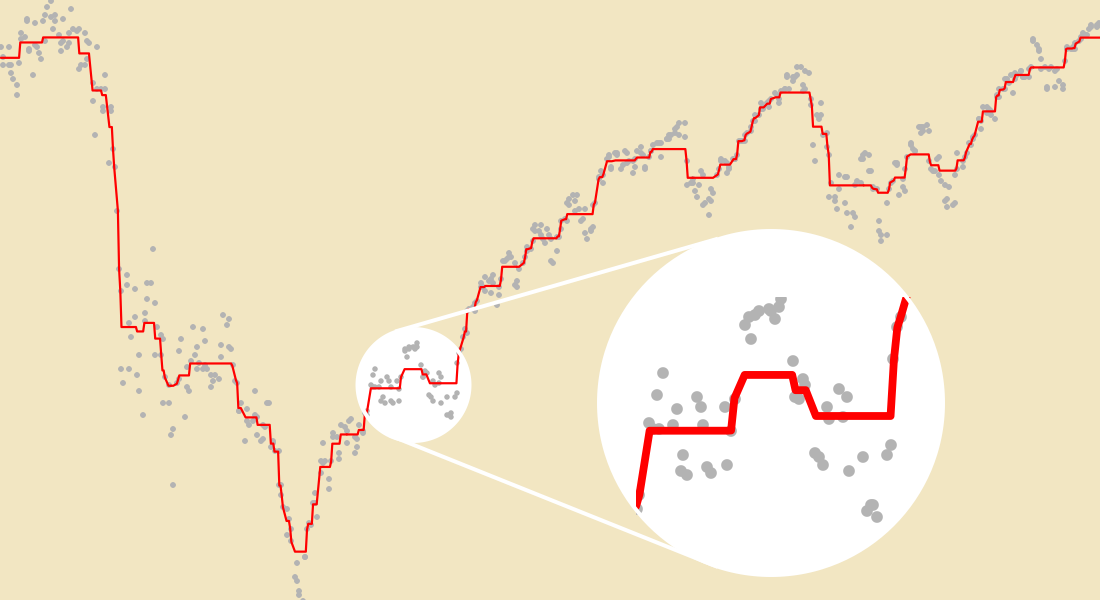
특수 목적의 최적화

전용 함수를 사용하여 중요한 최적화 작업을 쉽게 모델링하고 효율적으로 해결합니다. 직관적인 인터페이스를 사용하여 신경망 훈련 문제, 순회 세일즈맨 문제 및 배낭 문제를 포함한 특별한 최적화 문제를 해결합니다.

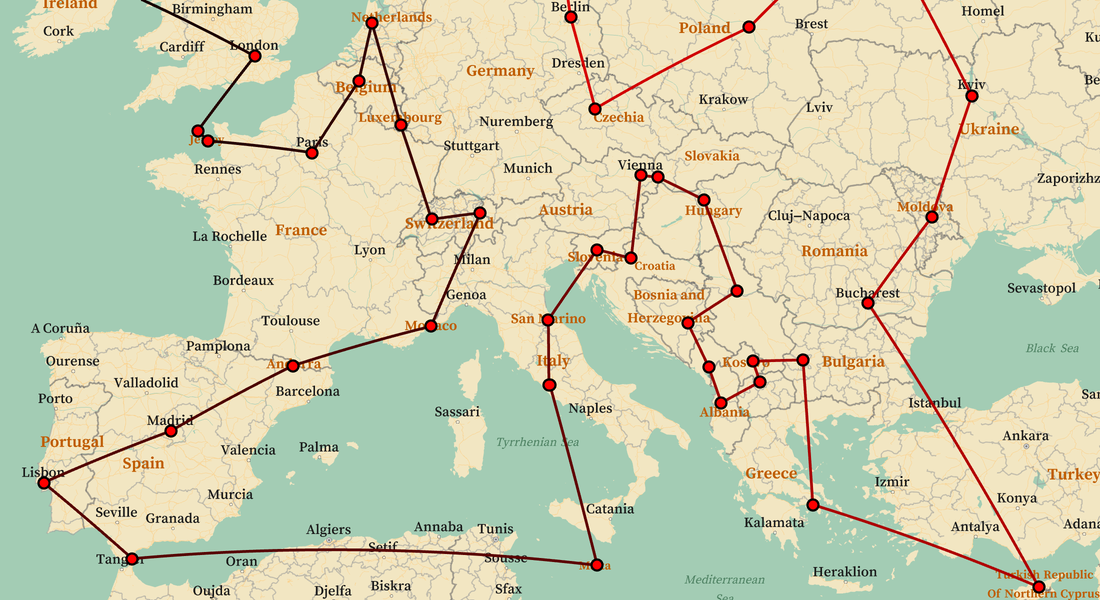
최적화 파트너

Gurobi, MOSEK, FICO Xpress의 상용 솔버를 직접 활용할 수 있습니다. 대규모 혼합 정수 최적화는 클래스 최고의 솔버를 지원합니다. 최적화 함수는 고객이 라이선스를 가지고 있는 방법을 자동으로 사용합니다.

Live Playground

This is an interactive notebook—try making your own changes!

Continue exploring more examples:Things to Try

최적화에 대한 Wolfram 문서

Wolfram 최적화은 Wolfram 언어의 통합된 부분입니다. 전체 시스템은 면밀히 통합되어 완벽하게 함께 작동하는 모든 계산 — 영역을 커버하는 6,000개 이상의 내장 함수가 포함되어 있습니다.

Wolfram 언어
전체 영역 및 문서

Predict ▪ Classify ▪ ActivePrediction ▪ SequencePredict ▪ Nearest ▪ FindClusters ▪ FeatureExtraction ▪ FeatureSpacePlot ▪ FeatureImpactPlot ▪ AnomalyDetection ▪ DimensionReduction ▪ MissingValueSynthesis ▪ LLMFunction ▪ LLMSynthesize ▪ ImageSynthesize ▪ ChatObject ▪ LLMPrompt ▪ LLMTool ▪ LLMConfiguration ▪ NetModel ▪ NetGraph ▪ LinearLayer ▪ ConvolutionLayer ▪ AttentionLayer ▪ ImageIdentify ▪ ImageCases ▪ FindFaces ▪ TextRecognize ▪ ImageGraphics ▪ TextSummarize ▪ LanguageIdentify ▪ TextStructure ▪ TextCases ▪ SpeechRecognize ▪ AudioIdentify ▪ SpeechCases ▪ SpeakerMatchQ ▪ PitchRecognize ▪ PseudoInverse ▪ Norm ▪ QRDecomposition ▪ SingularValueDecomposition ▪ Fit ▪ LinearModelFit ▪ NonlinearModelFit ▪ GeneralizedLinearModelFit ▪ LogitModelFit ▪ GeometricOptimization ▪ VectorGreaterEqual ▪ VectorLessEqual ▪ VectorGreater ▪ VectorLess ▪ NMinimize ▪ NMaximize ▪ FindMaximum ▪ FindFit ▪ Maximize ▪ MaxValue ▪ NMinValue ▪ NMaxValue ▪ FindMinValue ▪ FindMaxValue ▪ ArgMax ▪ NArgMin ▪ NArgMax ▪ FindArgMin ▪ FindArgMax ▪ LeastSquares ▪ ConvexOptimization ▪ ParametricConvexOptimization ▪ RobustConvexOptimization ▪ LinearOptimization ▪ LinearFractionalOptimization ▪ QuadraticOptimization ▪ SecondOrderConeOptimization ▪ SemidefiniteOptimization ▪ ConicOptimization ▪ FindShortestTour ▪ Minimize ▪ FindMinimum ▪ ArgMin ▪ MinValue ▪ KnapsackSolve ▪ FrobeniusSolve ▪ BayesianMinimization ▪ BayesianMinimizationObject ▪ BayesianMaximization ▪ BayesianMaximizationObject ▪ RegionPlot ▪ RegionPlot3D ▪ NetTrain ▪ SpherePoints ▪ EstimatedDistribution ▪ EstimatedProcess ▪ FindFormula ▪ FindGeometricTransform ▪ ImageAlign ▪ GuidedFilter ▪