Algèbre
Tu peux factoriser ou développer des expressions algébriques :
(Utilise CTRL+6 pour écrire les exposants).
| Out[1]= |  |
Wolfram Language utilise == (deux signes égaux) pour tester l'égalité :
| Out[1]= |  |
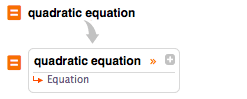
Combine des expressions algébriques avec == pour représenter une équation :
| Out[2]= |  |
Les commandes telles que Solve trouvent les solutions exactes aux équations :
Pour obtenir des résultats approximatifs, utilise NSolve :
Passe un système d'équations sous forme de liste :
Trouve les racines d'une équation :
(|| est le symbole pour Or).
| Out[1]= |  |
Si un polynôme n'est pas facilement factorisable, des résultats approximatifs peuvent être plus utiles :
| Out[2]= |  |
La commande Reduce réduit un ensemble d'inégalités à une forme simple :
(Tape <= pour le symbole ≤).
| Out[1]= |  |
La forme réduite peut comporter plusieurs intervalles :
| Out[2]= |  |
NumberLinePlot est un moyen pratique de visualiser ces résultats :
| Out[3]= |  |