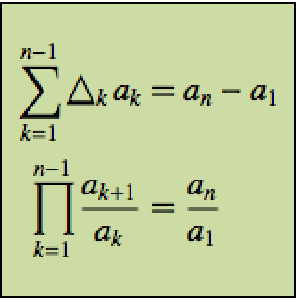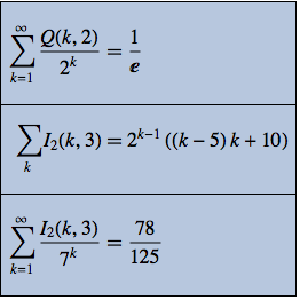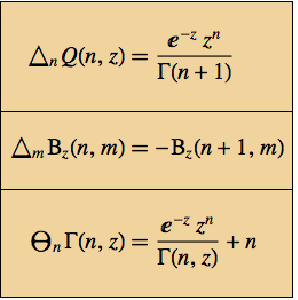Enhanced Calculus & Differential Equations
Version 10 adds many significant enhancements to its traditional strength in symbolic calculus. For the first time, symbolic solutions to hybrid differential equations with events and delay differential equations are possible. All discrete calculus operations are extended with newly developed algorithms motivated by probability and statistics. New dedicated commands for curve geometry as well as newly added special functions automate many tasks. Taken together, these developments will lead to smoother workflow for a wide range of applications, starting from college calculus to research level.
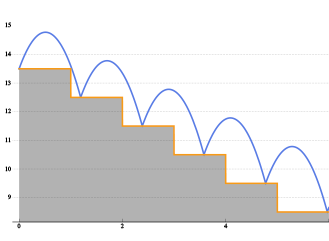
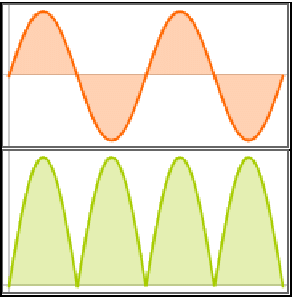
- Obtain symbolic solutions to hybrid differential equations, with explicit events. »
- Obtain symbolic solutions to delay differential equations.
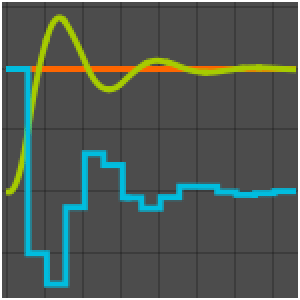
- Compute arbitrary expressions of solutions for differential equations. »
- Obtain elegant results for discrete calculus operations on special functions. »
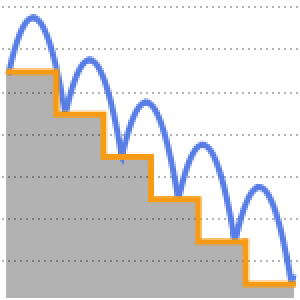
- Directly compute arbitrary expressions of solutions for difference equations. »
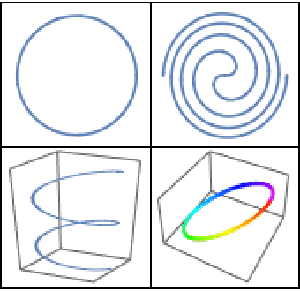
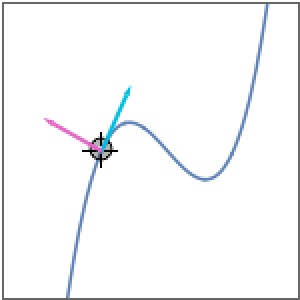
- Compute the curvature and arc length of parametrized curves. »
- Use the classical Frenet–Serret system for curves in n dimensions. »
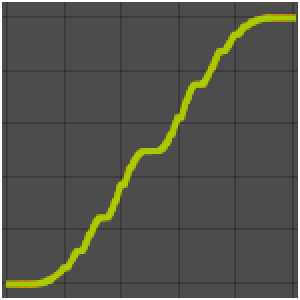
- New differential-equation-related functions, including Scorer, associated Fresnel, and logistic functions.
- Expanded number theoretic functions, such as generalized Dirichlet L-functions and the Riemann
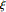 function. »
function. » - Play with fractals using Cantor staircase, Minkowski
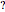 , and Böttcher functions. »
, and Böttcher functions. » - Construct interpolating functions from data with quantities. »
- Differentiate and integrate interpolating functions with quantities. »
- Use quantities in symbolic differential equations.