PDEs and Finite Elements
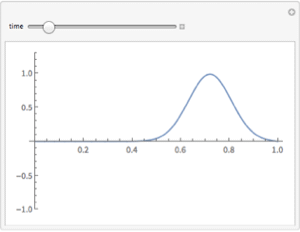
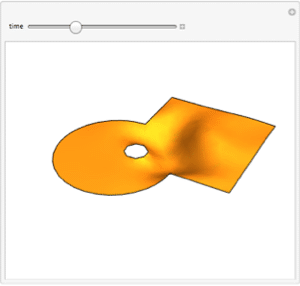
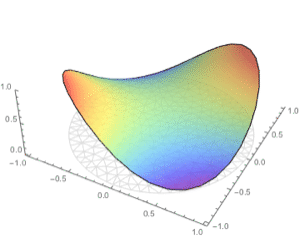
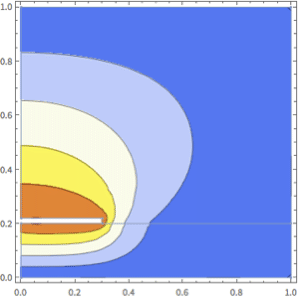
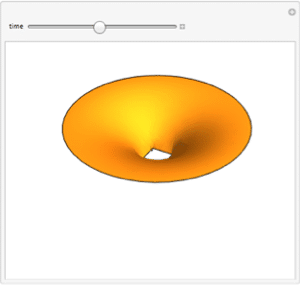
Version 10 extends its numerical differential equation-solving capabilities to include the finite element method. Given a PDE, a domain, and boundary conditions, the finite element solution process—including grid and element generation—is fully automated. Stationary and transient solutions to a single PDE or a system of partial differential equations are supported for one, two, and three dimensions.
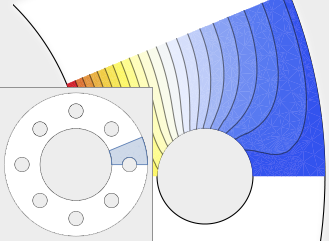
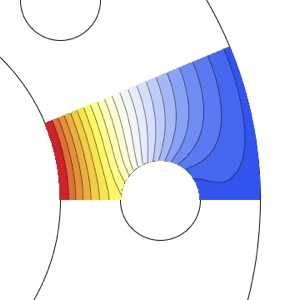
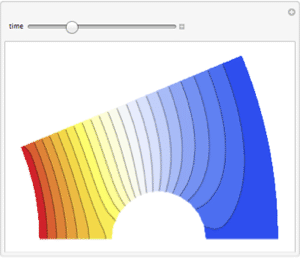
- Solve partial differential equations over arbitrarily shaped regions. »
- Solve stationary and transient PDEs in one, two, and three dimensions.
- Solve coupled systems of PDEs.
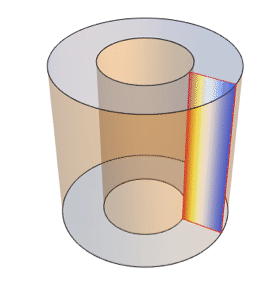
- Specify Dirichlet boundary conditions. »
- Specify generalized Neumann and Robin values. »
- Support for linear PDEs with coefficients that are variable in time and space.
- Freely formulate coupled PDEs for multiphysics analysis.
- Specify domains using the full geometric region framework.
- Fully automatic mesh generation from any region.
- Obtain solutions as approximate functions that can be further analyzed.
- Full suite of intermediate-level data structures and solution functions for detailed control and analysis of the solution. »
- Support for explicit mesh generation.
- Support for meshes with first- and second-order interpolation.
- Support for meshes with curved boundaries.
Related Examples
Solve the Telegraph Equation in 1D »
Solve a Wave Equation in 2D »
Solve Axisymmetric PDEs »
Solve PDEs over 3D Regions »
Dirichlet Boundary Conditions »
Neumann Values »
Generalized Neumann Values »
Solve PDEs with Material Regions »
Related FunctionsNDSolve 
NDSolveValue DirichletCondition NeumannValue DiscretizeRegion BoundaryDiscretizeRegion DiscretizeGraphics BoundaryDiscretizeGraphics TriangulateMesh BoundaryMesh MaxCellMeasure MeshQualityGoal MeshRefinementFunction
NDSolveValue DirichletCondition NeumannValue DiscretizeRegion BoundaryDiscretizeRegion DiscretizeGraphics BoundaryDiscretizeGraphics TriangulateMesh BoundaryMesh MaxCellMeasure MeshQualityGoal MeshRefinementFunctionRelated Guides
