Software Development
Explore the Details on the Mandelbrot Set
Because of the increase in the computational speed, computations that take a long time can now be computed in real time.
Explore details of the Mandelbrot set.
Because the computation is fast, visualizing the result is interactive.
Since Mathematica syntax is used, the turnaround speed is fast.
| In[1]:= | 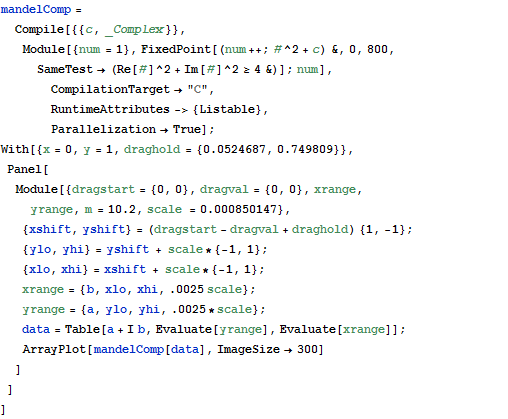 X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= | 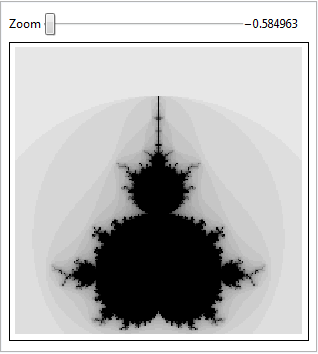 |
| In[3]:= |  X |
| Out[3]= | 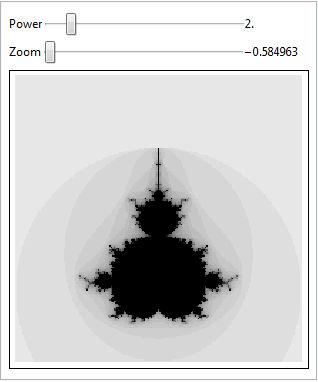 |