Software Development
Use Compile to Procedurally Generate Textures
Compile can be used to generate procedural textures that can be applied on objects.
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= | 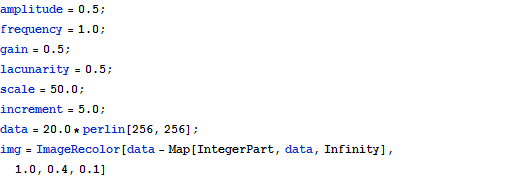 X |
| Out[3]= |  |
| In[4]:= |  X |
| Out[4]= |  |
| New in Wolfram Mathematica 8: Compiler Performance Enhancements | ◄ previous | next ► |
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= |  X |
| Out[3]= |  |
| In[4]:= |  X |
| Out[4]= |  |