Software Development
Integration with NDSolve
Mathematica functions can take C code as input. This shows NDSolve computing Duffing's equation using the Runge-Kutta method.
| In[1]:= | 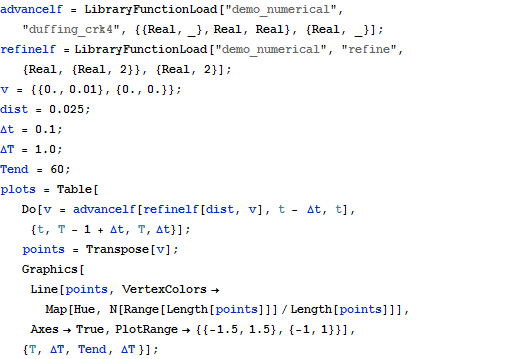 X |
| In[2]:= | X |
| Out[2]= | 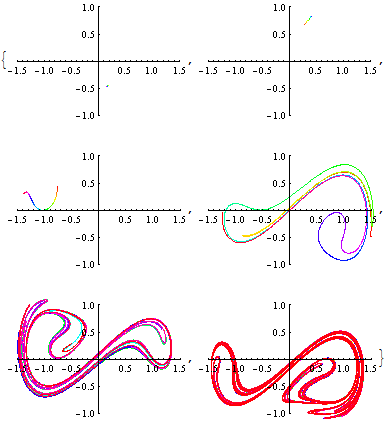 |
| New in Wolfram Mathematica 8: Dynamic Library Loading | ◄ previous | next ► |
| In[1]:= |  X |
| In[2]:= | X |
| Out[2]= |  |