Graphics & Visualization
Multiple Geometric Transformations on an Object
Apply multiple geometric transformations on a textured triangle to create a kaleidoscope.
| In[1]:= |  X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= | Play Animation » Stop Animation » 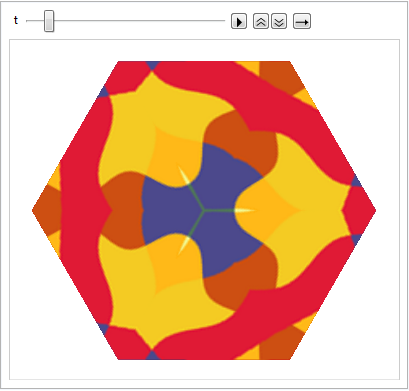 |
| New in Wolfram Mathematica 8: Enhanced 2D and 3D Graphics | ◄ previous | next ► |
| In[1]:= |  X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= | Play Animation » Stop Animation »  |