Integration with Wolfram|Alpha
Calculus and Special Functions
 (Ctrl+
(Ctrl+| In[1]:= |  X |
| Out[1]= | 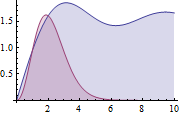 |
| In[2]:= | X |
| Out[2]= | 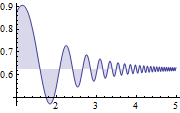 |
| In[3]:= |  X |
| Out[3]= |
| In[3]:= | X |
| Out[3]= |
| In[4]:= | X |
| Out[4]= |
| In[6]:= |  X |
| Out[6]= |
To get detailed information on your query, use double equal signs.
| In[7]:= | X |
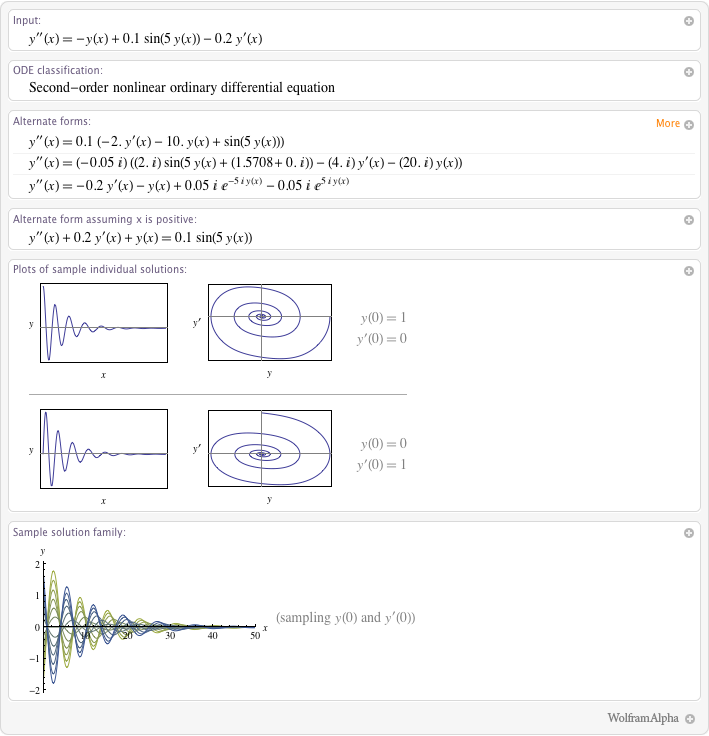 |