Application Areas
Find an Isomorphism
Find an isomorphism that maps two graphs.
| In[1]:= | X |
| In[2]:= | X |
| In[3]:= | X |
| In[4]:= | X |
| In[5]:= | X |
| In[6]:= | X |
| In[7]:= | X |
| In[8]:= |  X |
| In[9]:= |  X |
| In[10]:= | X |
| Out[10]= | 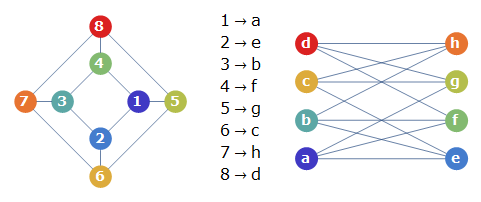 |
| New in Wolfram Mathematica 8: Graph & Network Analysis | ◄ previous | next ► |
| In[1]:= | X |
| In[2]:= | X |
| In[3]:= | X |
| In[4]:= | X |
| In[5]:= | X |
| In[6]:= | X |
| In[7]:= | X |
| In[8]:= |  X |
| In[9]:= |  X |
| In[10]:= | X |
| Out[10]= |  |