Application Areas
Perform a Depth-First Scan
Depth-first traversal of a hypercube.
| In[1]:= |  X |
| Out[1]= | Play Animation » Stop Animation » 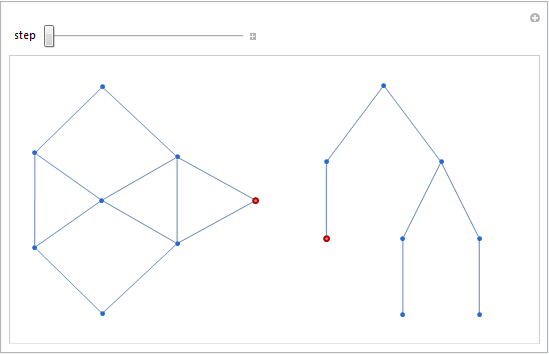 |
| New in Wolfram Mathematica 8: Graph & Network Analysis | ◄ previous | next ► |
| In[1]:= |  X |
| Out[1]= | Play Animation » Stop Animation »  |