Core Algorithms
Perform Numerical Hankel Transform
Hankel transform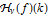 
is given by 
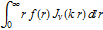. Hankel transform is computed numerically thanks to Mathematica 8's efficient algorithms for integration of oscillatory functions.
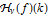is given by 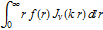. Hankel transform is computed numerically thanks to Mathematica 8's efficient algorithms for integration of oscillatory functions.| In[1]:= |  X |
| Out[1]= | 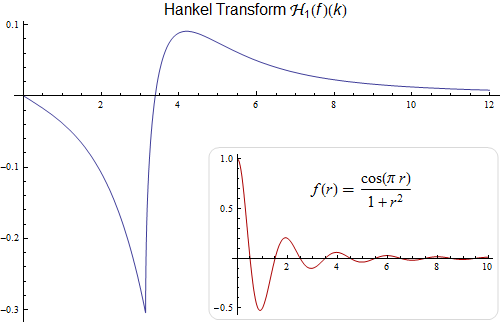 |