Core Algorithms
Solve High-Degree Real Polynomial Equations Numerically
This approximates real solutions of a sparse polynomial equation of degree one million.
| In[1]:= |  X |
| In[2]:= | X |
| Out[2]= | 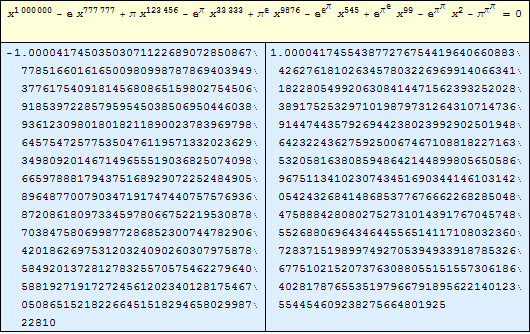 |
| New in Wolfram Mathematica 8: New and Improved Core Algorithms | ◄ previous | next ► |
| In[1]:= |  X |
| In[2]:= | X |
| Out[2]= |  |