Core Algorithms
Apply Censoring to a Distribution
The PDF and CDF of CensoredDistribution have discontinuities at the endpoints of the censoring interval, giving the distribution a mixed continuous-discrete character.
| In[1]:= |  X |
| In[2]:= |  X |
| In[3]:= |  X |
| Out[3]= | 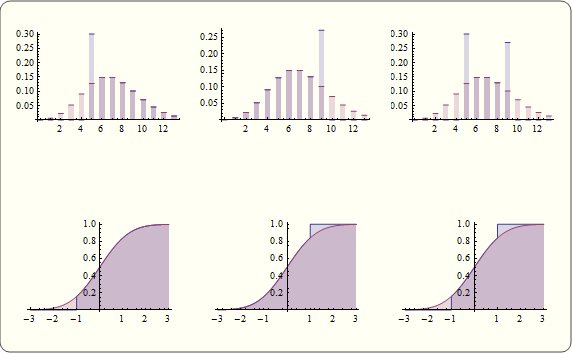 |