Core Algorithms
Estimate Multivariate Nonparametric Probabilities and Expectations
The PDF of a bivariate density estimate, using SmoothKernelDistribution, shown with the data it was created from and the expected values of successive power sums.
| In[1]:= |  X |
| In[2]:= | X |
| In[3]:= |  X |
| Out[3]= | 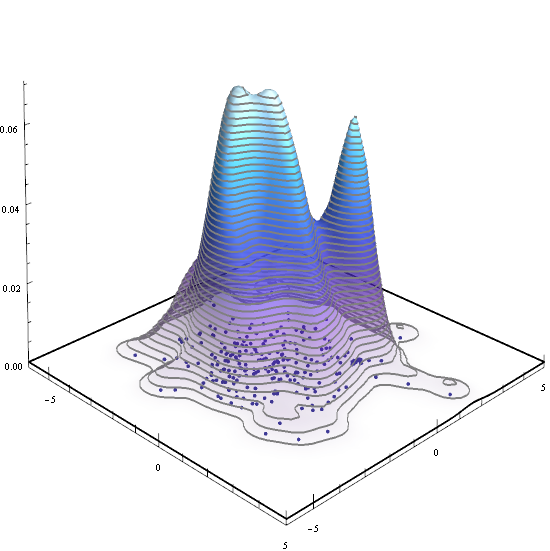 |
| In[4]:= | X |
| In[5]:= | X |
| Out[5]= |